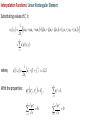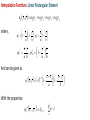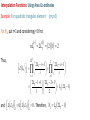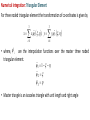Download Families of Shape Functions, Numerical Integration

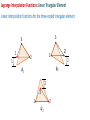
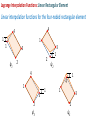
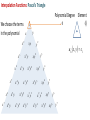
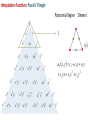
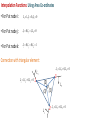
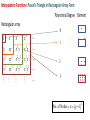
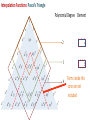
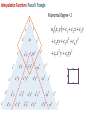
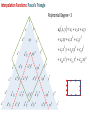
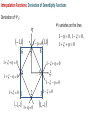
Families of Shape Functions, Numerical Integration,
Physical and Master Element, Concept and Mapping,
Element Stiffness and Load Vector Calculations
PM Mohite
Department of Aerospace Engineering
Indian Institute of Technology Kanpur
TEQIP School on Computational Methods
in Engineering Application
Knowledge Incubation for TEQIP
Two Dimensional Problems
Two Dimensional Problems:
 Single variable or multivariable problems
 The phenomenon is represented through partial differential equations
 Finite element formulation involves same steps as one dimensional case
 Boundary
of a two dimensional domain Ω, in general, is a curve
 Two dimensional shapes like triangle and rectangle/quadrilaterals are used to
approximate the geometry.
Sample Boundary Value Problems:
• Poisson equation
   ku   f
gradient operator
in 
 ˆ 
ˆ
i
 j
x
y
These equation represent
• Heat conduction
• Electrostatics
• Stream function
• Magnetic statics
• Torsion of non-circular sections, Transverse deflection of elastic membranes
Sample Boundary Value Problems: Heat Conduction
 
u
u   
u
u  
   k11
 k12
 k22
  f  x, y 
   k21

x
y  y 
x
x  
 x 
in 
with k12  k21  0and k11  k22  k it becomes Poisson’s equation.
Finite element discretization:
• The number, shape and type (linear, quadratic,……….) of elements should be
such that the geometry of the domain is accurately represented.
• Density of elements should be such that the regions of large gradients of the
solution are adequately modeled.
Heat Conduction Equation: Weak Formulation
Weighted residual form:
 
u
u   
u
u 
   x  k11 x  k12 y   y  k22 x  k22 y w dA   w dA
We know that,
q x

w
q x w  w  q x
x
x
x
Therefore,
Similarly,

w
 
 qx w  qx w  qx
x
x
 x 



w
 q y w  q y w  q y
y
y
 y 
Heat Conduction Equation: Weak Formulation
Now using the Divergence Theorem,

 x qx wdA   qx w nx ds
and

 y q y wdA   q y w ny ds
where nx and ny are the direction cosines or the components of the unit normal
vector n
n  nx iˆ  ny ˆj  cos  iˆ  sin  ˆj
Heat Conduction Equation: Weak Formulation
writing the weak form over an element
 w  u

u  w 
u
u 
 
 k 21
  wf  dA
0     k11
 k12
 k 22
x  x
y  y 
x
y 

e 
 

u
u 
u
u 
  n y  k 21
 ds
  e wnx  k11
 k 22
 k 22

x
y 
x
y 

 
Looking at boundary term:
• wu 
Primary variable – essential BC and
• coefficient of weight function in boundary term form the natural BC.
Heat Conduction Equation: Weak Formulation
 u
 u
u 
u 
  n y  k21

qn  nx  k11
 k12
 k22
y 
x
y 
 x

on e
qn - is the secondary variable.
qn - projection of the vector k u along the unit normal n
- positive outward from the surface as the as we more counter-clock wise along
the boundary
Thus,
 w  u

u  w  u
u 
0    k11  k12    k21  k22   wf  dA  wqn ds
x  x
y  y 
x
y 

e 


e


Heat Conduction Equation: Weak Formulation
Or
Bw, u   F w
where,
 w  u
u  w  u
u 
 k 21  k 22  dA
Bw, u      k11  k12  
x  x
y  y  x
y 
e 
F w   e w f dA   e wq n ds


Bw, u  - bilinear from, is not symmetric. It is symmetric only when k12  k21
F  w  - linear from
Quadratic Potential:
I  u   B  u, u   F  u 
Heat Conduction Equation: Finite Element Formulation
Approximation of
u over
 e as
u  x, y   uh  x, y  
NODE

j 1
u ej
 x, y 
e
j
u ej - are the nodal values of at node.

e
j
- are the Lagrange interpolation functions with the property  ie  x j , y j    ij
Substitute uh  x, y  
replace w
0
by  ie to
NODE 
 
j 1

   i
 
e  x
 f
e
i
NODE

u ej  ej  x, y 
j 1
in the weak form and to get equation
give
 j   i
  j
 k12
 k11
 
x
y  y

dA   i qn ds
e
 j
 j  

 k22
 k21
  dA
x
y  

i, j  1, 2,
, NODE
Heat Conduction Equation: Finite Element Formulation
This leads to:
NODE

kije u ej  fie  Qie
j 1
where,
  i   j
 j   i   i
 j 
 k11
 
 k 21
 dA
k  
 k12
 k 22
x 
x
y  y 
x
y 
e 
e
ij
fi e 
and

f  ie dA,
e
In matrix notation,
k 
e
Qie   qn  ie ds
e
k u  f  Q 
e
e
e
is symmetric only when k12  k 21
e
Interpolation Functions in Two Dimensions
Interpolation Functions: Requirements
The approximate solution u h  x, y 
over an element, for the assurance of
convergence to the actual solution as the number of elements is increased and
their size is decreased, must satisfy:
1) It must be continuous over the element and differentiable as required by the
weak form.
- It ensures a nonzero coefficient matrix
2) It must not allow a strain to appear if the nodal displacements are compatible
with a rigid-body displacements.
Interpolation Functions: Requirements
3) If the nodal displacements are compatible with a uniform strain in the
elements, then the interpolation functions must yield this strain for the nodal
displacements.
In other fields:
If the nodal variables are compatible with uniform states of the variable  and
any of its derivatives up to the highest in the appropriate quadratic functional
I   , then these uniform states must be preserved in the element as it shrinks
to zero size. This condition is called completeness.
- This requirement is necessary in order to capture all possible states of the
actual solution
Interpolation Functions: Requirements
Example:
If a linear polynomial without the constant term is used to represent the
temperature distribution in a one-dimensional system, the approximate solution
can never be able to represent a uniform state of temperature in the element.
Interpolation Functions: Requirements
4) The interpolation functions should be chosen so that the strain remains finite at
the boundary. Note, however, that the strain can be indeterminate at a boundary.
For example, if the strains involve only the first derivatives, then the displacement
field must be continuous across a boundary. (strain energy must be finite)
In other fields:
The dependent variable and all its derivatives up to a one less than the highest
order derivative in the appropriate quadratic functional should be continuous at
the element interfaces. (The quadratic potential must be finite)
This requirement is called compatibility condition.
Elements satisfying these requirements are called conforming elements.
Interpolation Functions: Requirements
Degree of Compatibility achieved by interpolation functions at the element:
• C 0 continuity is achieved when the field variable only and none of its derivatives
maintain continuity at an interelement interface.
• C1 continuity is achieved when the field variable and its first derivatives maintain
continuity at an interelement interface.
• C 2 continuity is achieved when the field variable, its first derivatives and second
derivatives all maintain continuity at an interelement interface.
Interpolation Functions: Requirements
Continuity Requirement for completeness and compatibility:
For assurance of finite element convergence for a functional having p as the
highest order of a derivative –
• C p continuity – requirement for completeness
• C  p 1 continuity – requirement for compatibility
Interpolation Functions: Types of Families
Lagrange Family:
• Interpolation functions derived using the dependent unknown only and not its
derivatives, at nodes.
• C 0 - continuity
Hermite Family:
• Interpolation functions derived using the dependent unknown and its derivatives
as well, at nodes.
• C1 continuity – continuity of the first derivative of the dependent unknown.
Cubic interpolation functions
• C 2 continuity – continuity of the first and second derivatives of the dependent
unknown. Quintic interpolation functions
Linear Interpolation Functions:
 ie must be at least linear in x and y.
Let
uh x, y   c1  c2 x  c3 y
 Three linearly independent terms, linear in both x and y.

ci to be expressed terms of nodal values of u h . Hence, we must have three
nodes.
 This is possible for a triangle with its vertices as nodes.
Linear Interpolation Functions:
• Consider a polynomial
uh x, y   c1  c2 x  c3 y  c4 xy
• Four linear independent terms, linear in x, y with a bilinear term in x and y.
• This requires an element with four nodes.
• Two possible geometries:
- A triangle with the three nodes at its vertices and the fourth node at its
centre or centroid.
- A rectangle with the nodes at the vertices
Linear Interpolation Functions:
• A triangle with the fourth node at its centre does not provide a single valued
variation of primary variable at interelement boundaries.
• This results in incompatible variations of primary variable there. Therefore, this
is not admissible.
• Thus, the only possible element with assumed polynomial approximation is
rectangle with the nodes at the four vertices
Quadratic Interpolation Functions:
• Consider a polynomial with five constants

uh x, y   c1  c2 x  c3 y  c4 xy  c5 x 2  y 2

• This is an incomplete quadratic polynomial
• Note that the terms x2 and y2 can not be varied independently.
• The polynomial requires an element with five nodes.
• The possible geometry is a rectangle with a node at each vertex and the fifth
node at its centre.
• This again does not give single valued variation of primary variable.
Quadratic Interpolation Functions:
• Consider a polynomial with six constants
uh x, y   c1  c2 x  c3 y  c4 xy  c5 x 2  c6 y 2
• This is a complete quadratic polynomial
• The polynomial requires an element with six nodes.
• The possible geometry is a triangle with a node at each vertex and a node at the
midpoint of each side.
Lagrange Interpolation Functions
in Two Dimensions
Linear Interpolation Functions
in Two Dimensions
Interpolation Functions: Linear Triangular Element
A triangular element with three nodes at vertices
3
1
2
Approximate solution over an element is of the form
uh x, y   c1  c2 x  c3 y
We need three conditions to find the unknowns Ci ‘s.
Using nodal values of solution we get three conditions
Interpolation Functions: Linear Triangular Element
Thus, we have
Or in a matrix form
u1  uh x1 , y1   c1  c2 x1  c3 y1
u2  uh x2 , y2   c1  c2 x2  c3 y2
u3  uh x3 , y3   c1  c2 x3  c3 y3
u1  1 x1
  
u2   1 x2
u  1 x
3
 3 
y1   c1 
 c1 
 
 

y2  c2   Ac2 

c 
y3  
c
 3
 3
unknowns Ci ‘s are found as
u1   c1 
A1 u2   c2 
u  c 
 3  3
where,
1  2  3 
1 
1
A  1  2 3 
2 Ae
 1  2  3 
2 Ae  1   2   3
Interpolation Functions: Linear Triangular Element
Solving for Ci ‘s:
1
1u1   2u2   3u3 
c1 
2 Ae
1
1u1   2u2  3u3 
c2 
2 Ae
1
 1u1   2u2   3u3 
c3 
2 Ae
- determinant of A
Ae - area of the triangle
2 Ae
where,
 i  x j y k  xk y j 

 i  y j  yk
 i  j  k and i, j , k permute in a natural order
 i  x j  xk  
Interpolation Functions: Linear Rectangular Element
Substituting values of Ci ‘s:
u h  x, y  
1
1u1   2u2   3u3   1u1   2u2   3u3 x   1u1   2u2   3u3  y 
2 Ae
3
  uie ie  x, y 
i 1
where,
1

 x, y  
 ie  ie   ie  i  1,2,3
2 Ae
e
i
With the properties:

e
i
x
e
j
,y
e
j
 
 ie
 0,

x
i 1
3
3
ij ,
e

 i  1,
i 1
 ie
0

y
i 0
3
Lagrange Interpolation Functions: Linear Triangular Element
Linear interpolation functions for the three-noded triangular element
3
3
1
1
2
1
2
1
ψ2
ψ1
1
3
2
1
ψ3
Lagrange Interpolation Functions: Triangular Geometries to Avoid
• The nodes are almost in-line.
• The resulting coefficient matrix is nearly singular or non-invertible.
a
L>>a
L
L>>h
h
L
Lagrange Interpolation Functions: Linear Triangular Element
Shapes that should be avoided in the meshing.
Interpolation Functions: Linear Rectangular Element
A rectangular element with four nodes at the corner and of sides a and b.
y
y
b
4
3
1
2
a
x
x
Approximate solution over an element is of the form
uh x , y   c1  c2 x  c3 y  c4 x y
We need four conditions to find the unknowns Ci ‘s.
Interpolation Functions: Linear Rectangular Element
Using the nodal solution values, we get four conditions:
uh 0,0  u1  c1
uh a,0  u2  c1  a c2
uh a, b   u3  c1  c2 a  c3 b  c4 ab
uh 0, b   u4  c1  c3 b
Gives the values of constants as
u3  u4  u1  u2
u2  u1
u4  u1
c1  u1 , c2 
, c3 
, c4 
a
b
ab
Putting these back and re-arranging,
x y xy 

x x y
x y
 y x y
uh x , y   u1 1   
  u2  
  u3 
  u4  

a b ab 

a a b
a b
b a b
Interpolation Functions: Linear Rectangular Element
uh  x , y   u1 2  u2 2  u3 3  u4 4
where,
x 
y e x
x

  1  1  ,  2  1  
a 
b
a b

e
1
 3e 
x y
x  y

,  4e  1 

a b
a b

And can be given as
 x , y    1
e
i
With the properties:
i 1
x  xi  
y  yi 

1 
 1 

a 
b 

 ie x j , y j    ij ,
4
e

 i 1
i 1
Lagrange Interpolation Functions: Linear Rectangular Element
Linear interpolation functions for the four-noded rectangular element
4
4
1
1
1
3
3
ψ1
2
2
1
ψ2
4
1
4
1
3
2
ψ3
1
1
3
2
ψ4
Interpolation Functions: Linear Rectangular Element
• Can also be obtained from tensor product of 1D linear interpolation functions
associated with sides 1-2 and 2-3
 x  y  e x  x  e x y
 x
e
  1  1  ,  2  1  ,  3 
,  4  1 
a b
ab
 a  b 
 a
e
1
1
x
a
y

b
1
x
a
x
b
a
 x
1  a 
y
 x 1 

 b
 a 
y   1

b   2
4
 3 
y
b
y
y
b
Interpolation Functions: Linear Rectangular Element
Another approach:
Derivation of  1e x , y 
We know that  1e x1 , y1   1
and  1e xi , yi   0
for i  2,3,4
And zero on the lines x  a and y  b
Therefore,
 1e
is of the form:
Putting first condition that
Hence,  1e is
 1e  x , y   c1 a  x b  y 

e
1
x , y   1 at
x  0, y  0
1
x 
y

a  x b  y   1  1  
 x , y  
ab
b
 a 
e
1
In a similar way, the other interpolation functions can be derived.
1
 c1 
ab
Higher Order Interpolation Functions
For Triangular Element
Interpolation Functions: Higher Order Element
• The interpolation functions of higher degree can be systematically developed
with the help of Pascal’s Triangle.
• It contain the terms of polynomials of various degrees in the two coordinates x
and y.
• x and y denote the local coordinate (and not the global coordinates of the
problem).
• Shape of the triangle need not be equilateral triangle.
• p th order triangular element has n nodes given by the relation
1
n   p  1 p  2 
2
th
p
• A complete polynomial of
degree is given by
n
n
u ( x, y )   ai x r y s   u j j
i 1
j 1
with r  s  p
Interpolation Functions: Pascal’s Triangle
1
y
x
x2
x
x4
x5
x6
x7
x6 y
x5 y
2
3
x y
x3 y
x4 y
x4 y2
y3
xy 2
x y
3
xy 5
x2 y4
3
x y
y5
xy 4
x2 y3
x3 y3
4
y4
xy 3
x2 y2
x3 y 2
x5 y 2
y2
xy
4
2
x y
5
y6
xy
6
y7
Interpolation Functions: Pascal’s Triangle
Polynomial Degree
1
We choose the terms
y
in the polynomial
x
x2
x
x4
x5
x6
x7
x6 y
x5 y
x y
x3 y
x4 y
x4 y2
x5 y 2
y2
x y
3
y4
xy 3
xy 5
x2 y4
3
x y
y5
xy 4
x2 y3
x3 y3
4
u h  x, y   c1
y3
xy 2
x2 y2
x3 y 2
1
0
xy
2
3
Element
4
2
x y
5
y6
xy
6
y7
Interpolation Functions: Pascal’s Triangle
Polynomial Degree
Element
1
y
x
x2
x
x4
x5
x6
x7
x6 y
x5 y
x y
x3 y
x4 y
x4 y2
x y
3
y4
xy 3
xy 5
x2 y4
3
x y
y5
xy 4
x2 y3
x3 y3
4
uh x, y   c1  c2 x  c3 y
y3
xy 2
x2 y2
x3 y 2
x5 y 2
y2
xy
2
3
1
4
2
x y
5
y6
xy
6
y7
3
Interpolation Functions: Pascal’s Triangle
Polynomial Degree
Element
1
y
x
x2
x
x
x5
x6
x7
x6 y
x5 y
4
2
x y
x4 y
x y
2
x3 y 2
x4 y2
x5 y 2
y3
xy 2
x y
3
xy
x y
3
3
y
x y
 c4 xy  c5 x 2  c6 y 2
y5
xy 5
x2 y4
3
uh  x, y   c1  c2 x  c3 y
4
xy 4
x2 y3
x3 y3
4
6
y2
xy
2
3
2
4
2
x y
5
y6
xy
6
y7
Interpolation Functions: Pascal’s Triangle
Polynomial Degree
1
We choose the terms
y
in the polynomial
x
x2
x
x4
x5
x6
x7
x6 y
x5 y
2
3
x y
x3 y
x4 y
x4 y2
x5 y 2
y2
y3
xy 2
x y
3
xy 5
x2 y4
3
x y
y5
xy 4
x2 y3
x3 y3
4
y4
xy 3
x2 y2
x3 y 2
1
1
3
2
6
3
10
4
15
5
21
28
0
xy
4
2
x y
5
y6
xy
6
6
y7
Element
7
1
n   p  1 p  2 
2
Lagrange Interpolation Functions: Quadratic Triangular Element
Geometric variation of Lagrangian interpolation functions
Interpolation Functions For Triangular Element
using Area Coordinates
Interpolation Functions: Using Area Co-ordinates
P is an arbitrary point inside a linear triangular element
k
i
(j)
P (i)
(k)
j
Let Ai, Aj and Ak be the area of triangles formed by point P with an edge of the
triangle.
For example, Ak is the area formed by edge i-j and point P.
Define: Natural /triangular/ barycentric coordinate
Aj
Ai
A
Li 
, Lj 
, Lk  k
A
A
A
and
Li
A  Ai  Aj  Ak
Interpolation Functions: Using Area Co-ordinates
• For P at node i:
Li  1, L j  0, Lk  0
• For P at node j:
Li  0, L j  1, Lk  0
• For P at node k:
Li  0, L j  0, Lk  1
Connection with triangular element:
L3  1, L1  0, L2  0
L3
L1  1, L2  0, L3  0
1
(2)
P (1)
(3)
L1
2
3
L2
L2  1, L1  0, L3  0
Interpolation Functions: Using Area Co-ordinates
• We needed to invert coefficient matrix when we derived interpolation functions.
This can be avoided in this approach.
6
3
1
Consider a quadratic triangular element
(2)
P(1)
(3)
5
We express natural co-ordinate Li at any point
4
by using superscript to identify the nodes.
2
Example: Point P moves to node 6.
1
L16  
A1 1
 ,
A 2
L26  
A2 0
  0,
A A
L36  
A3 1

A 2
4
6
3
P
(3) (1) 5
2
Interpolation Functions: Using Area Co-ordinates
• Point P moves to node at 4.
A 1
L1  1  ,
A 2
4 
A
1
L2  2  ,
A 2
4 
6
A
0
L3  3   0
A A
4 
1
(2)
4 P
• Point P moves to node at 5.
A1 0
L1 
  0,
A A
5 
L25  
A2 1
 ,
A 2
3
(1) 5
2
L35  
A3 1

A 2
6
(2)
1
4
3
P
(3)
2
5
Interpolation Functions: Using Area Co-ordinates
• For a cubic triangular element
1
4
Example: Point P moves to node 10.
10 
L1
A1 1

 ,
A 3
10 
L2
A2 1

 ,
A 3
L310  
A3 1

A 3
1
8
9
(2)
4 P
5
10 7
(1)
6
2
4
3
L1 4  
(2)
P 10 7
(3) (1)
6
5
2
9
1
Example: Point P moves to node 4.
A1 2
 ,
A 3
L24  
A2 1
 ,
A 3
A3 0
L3 
 0
A A
4 
8
9
3
8
(2)
P 10 7
(3) (1)
6
5
2
3
Interpolation Functions: Using Area Co-ordinates
To get the interpolation functions, we first transform the Lagrangian interpolation
formula from Cartesian to natural coordinates.
 
L Lj  

r
 
r 
nL j

i 1
L Lj   1

r
where
 nL j  i  1 


i


r 
for nL j  1
r 
for nL j  0
j = one of the three natural coordinates
n (=p) = order of interpolation polynomial
r = free index from 1 up to the total number of nodes
Thus, for each node:
N r   L  L1   L  L2   L  L3 
r
r
r
Interpolation Functions: Using Area Co-ordinates
Example: For quadratic triangular element
(n=p=2)
For N1, put r=1 and considering j=1 first
r 
1
nL j  2 L1   2 1  2
Thus,
 L  L1   
1
1
2 L1

i 1
 2 L1  i  1 



i


2

i 1
 2 L1  i  1 


i


 2 L1  1  1  2 L1  2  1 

 L1  2 L1  1


1
2



and  L  L2 1  0,  L  L3 1  0 . Therefore, N1  L1  2L1  1
Interpolation Functions: Using Area Co-ordinates
Example: For quadratic triangular element
(n=p=2)
For N4, put r=4 and considering j=1 first
r 
 4
nL j  2 L1
Thus,
 L  L1  
4
 4
2 L1

i 1
Now, considering j=2
 2 L1  i  1 



i


r 
1

i 1
 4
nL j  2 L2
1
  2    1
2
 2 L1  i  1   2 L1  1  1 

 2 L1



i
1

 

1
  2    1
2
 L  L2   2 L2
4
Interpolation Functions: Using Area Co-ordinates
Example: For quadratic triangular element
(n=p=2)
For N4, considering j=3
r 
 4
nL j  2 L3   2  0   0
 L  L3   1
4
Thus, N 4  4 L1 L2
For remaining nodes,
N 2  L2  2 L2  1 , N 3  L3  2 L3  1 ,
N 5  4 L2 L3 ,
N 6  4 L1 L3
Higher Order Interpolation Functions
For Rectangular Element
Interpolation Functions: Pascal’s Triangle
Polynomial Degree = 1
1
y
x
x2
x
x
x
x7
x y
x3 y3
x4 y3
xy
y4
3
x2 y3
x3 y 2
2
y3
2
x2 y2
x4 y2
5
xy
x y
x4 y
x5 y
x6 y
2
x3 y
4
5
x6
3
uh  x, y   c1  c2 x  c3 y  c4 xy
y2
xy
x2 y4
x3 y 4
y5
xy 4
y6
xy 5
2
x y
5
xy
6
y7
Interpolation Functions: Pascal’s Triangle
Polynomial Degree = 2
1
x2
x
x
x
x7
x6 y
5
x y
x3 y3
x4 y3
2
y4
3
x2 y3
x3 y 2
2
xy
y5
xy 4
x2 y4
x3 y 4
2
 c7 x y  c8 xy  c9 x y
y3
2
x2 y2
x4 y2
x5 y
xy
x y
x4 y
 c4 xy  c5 x  c6 y
2
y2
xy
2
x3 y
4
5
x6
3
uh x, y   c1  c2 x  c3 y
y
x
y6
xy 5
2
x y
5
xy
6
y7
2
2
2
Interpolation Functions: Pascal’s Triangle
Polynomial terms
can be chosen
Polynomial Degree = 3
1
x
x2
x
x6
x7
5
x y
2
x4 y3
 c10 x 3  c11 x 3 y  c12 x 3 y 2
y
xy 3
x2 y3
x3 y3
 c7 x 2 y  c8 xy 2  c9 x 2 y 2
y3
2
2
x3 y 2
x4 y2
x5 y
x6 y
x y
x y
x4 y
5
xy
x y
2
 c4 xy  c5 x 2  c6 y 2
y2
xy
2
3
x4
x
3
uh  x, y   c1  c2 x  c3 y
y
x3 y 4
y5
xy 4
x2 y4
 c13 x 3 y 3  c14 y 3  c15 xy3  c16 x 2 y 3
4
y6
xy 5
2
x y
5
xy
6
y7
Interpolation Functions: Pascal’s Triangle
Polynomial terms
can be chosen
Polynomial Degree Element
1
1
y
x
x2
x
x
x
x7
x4 y
2
x y
x y
5
x y
2
2
y3
xy
3
3
2
x y
x3 y 4
y
3
4
3
4
y5
xy 4
x2 y3
x y
x4 y3
2
2
2
x3 y 2
4
x y
xy
x y
x y
5
x6 y
2
3
4
5
x6
3
y2
xy
xy
2
x y
5
4
5
y
xy
6
No. of Nodes  n   p  1
6
y7
2
Interpolation Functions: Pascal’s Triangle in Rectangular Array Form
Polynomial Degree Element
Rectangular array
0
1
x
x2
x3
y xy x 2 y x 3 y
2
2
2 2
3 2
y xy x y x y
y 3 xy3 x 2 y 3 x 3 y 3









1
2
3
No. of Nodes  n   p  1
2
Interpolation Functions: Higher Order Rectangular Elements
The Lagrange interpolation functions associated with rectangular elements can be
obtained from corresponding one-dimensional Lagrange interpolation functions
by taking tensor product.
 1

 2

 3
4
5
6


a
x

(
x

a
)



2




T
b
   a (  a )   y  2 ( y  a ) 




b2


2


2
7 



x
(
x

a
)
y
(
y

b
)




 8    1


b2
1 a  a)
a
(

4


 9   2 x( x2 a )
b
y( y  2) 


2



b2
a( 12 a)
2










Interpolation Functions: Master Rectangular Elements
Tensor product of 1D functions:


 1,1
4
 1,1
1,1
3

1
1,1
1
1
 1  1   1   ,  2  1   1   ,
4
4
1
1
 1  1   1   ,  4  1   1   
4
4
2
1,1
7
8
4
5
3
1,1
1 2
 
4
1 2
6 
 
2
1 2
9 
 
4
   ,
1   ,
   
1,1












1 2
1
    2  ,  2  1   2
4
2
1 2
1
4 
   1  2 ,  5  1   2
2
4
1 2
1
7 
    2  ,  8  1   2
4
2
1 
   ,
1   ,
    ,
2
2
2

6
2
1
1,1
9
3 



2
2
2
Lagrange Interpolation Functions: Quadratic Rectangular Element
Geometric variation of Lagrangian interpolation functions
Lagrange Interpolation Functions: Quadratic Rectangular Element
Geometric variation of
Lagrange interpolation
functions:
Hermite Interpolation Functions: Master Rectangular Element
• The shape function presented earlier are for the interpolation of primary
variables.
• The Hermite cubic interpolation functions based on the interpolation of
can be generated.
u u  2u
u,
Interpolation for
Variable u
derivative u

x
,
y
,
xy
1
2
2
  i  i  2   i  i  2 
16
1
2
2

i   i  i  1  i  i  2 
16
Hermite Interpolation Functions: Master Rectangular Element
Derivative
u

 2u
Derivative

1
2
2

  i  i  2 i   i  i  1
16
1
2
2
i   i  1  1i   i  i  1
16
where, i=1,….4 are the nodes of the element.
Serendipity Family of Interpolation Functions
For Rectangular Element
Interpolation Functions: Pascal’s Triangle
Polynomial Degree Element
1
y
x
x2
x
x
x
x7
x4 y
2
x y
x y
2
y3
xy
y
3
x2 y3
x3 y3
x4 y3
2
2
2
x3 y 2
x4 y2
5
xy
x y
x y
x5 y
x6 y
2
3
4
5
x6
3
y2
xy
x3 y 4
y5
xy 4
x2 y4
3
4
4
y6
xy 5
2
x y
5
xy
6
y7
Terms inside this
cone are not
included
Interpolation Functions: Pascal’s Triangle
Polynomial Degree = 2
1
x2
x
x
x
x7
x6 y
5
x y
2
x3 y3
x4 y3
xy
2
y4
3
x2 y3
x3 y 2
 c7 x y  c8 xy
y3
2
x2 y2
x4 y2
x5 y
xy
x y
x4 y
 c4 xy  c5 x  c6 y
2
y2
xy
2
x3 y
4
5
x6
3
uh x, y   c1  c2 x  c3 y
y
x
x2 y4
x3 y 4
y5
xy 4
y6
xy 5
2
x y
5
xy
6
y7
2
2
Interpolation Functions: Pascal’s Triangle
Polynomial Degree = 3
1
x
x
x
x
x6
x7
x6 y
x y
xy
x3 y3
x4 y3
y
xy
 c7 x y  c8 xy  c9 x
2
3
x2 y4
x3 y 4
y5
xy 4
y6
xy 5
2
x y
5
2
3
 c10 x 3 y  c11 y 3  c12 xy3
y4
3
x2 y3
x3 y 2
2
 c4 xy  c5 x 2  c6 y 2
2
2
x2 y2
x4 y2
5
y
x y
x4 y
x5 y
xy
2
x3 y
4
5
2
3
uh  x, y   c1  c2 x  c3 y
y
x
xy
6
y7
Interpolation Functions: Pascal’s Triangle
Polynomial terms
can be chosen
Polynomial Degree Element
1
y
x
x2
x
x
x
x7
x4 y
2
x y
x y
2
y3
xy
y
3
x2 y3
x3 y3
x4 y3
2
2
2
x3 y 2
x4 y2
5
xy
x y
x y
x5 y
x6 y
2
3
4
5
x6
3
y2
xy
x3 y 4
y5
xy 4
x2 y4
3
4
4
y6
xy 5
2
x y
5
xy
6
y7
Interpolation Functions: Derivation of Serendipity Functions
Derivation of  1 :
 1 vanishes on the lines

 1,1
6
 
1   0 1,1
7
8
1     0
1     0
1   0
1    0, 1    0,
1     0
1     0
4
2
1
1,1 1   0
5

1     0
3 1   0
1,1
Interpolation Functions: Derivation of Serendipity Functions
Therefore,  1 is of the from
1  ,   C 1   1  1     
It has a value of 1 at  1, 1  c  1
4
1
 1   1   1   1     
4
 2 vanishes along the lines 1    0,1    0,1   0
Let
 2  c 1   1   1   
 2  1 at  0,-1  c 
1
2
2

1

1  2
2
 1   
Interpolation Functions: Derivation of Serendipity Functions
Similarly,
 3  14 1   1    1     
4 
1
4
5 
1
2
1    1 
1    1 
2
2


1   1    1     
 7  12 1   2  1   
 8  14 1   1    1     
6 
1
4
Note: The serendipity interpolation functions are different than Lagrange
interpolation functions as internal nodes are not present.
Hierarchic Interpolation Functions
For Rectangular Element
Interpolation Functions: Hierarchic Functions
• The set of interpolation functions of polynomial degree p should be in the set of
interpolation functions of polynomial degree (p+1).
• The number of interpolation functions which do not vanish at vertices and sides
should be smallest possible.
• Example: 1D Hierarchic interpolation
functions
Hierarchic Shape Functions: Rectangular Elements
• Nodal Interpolation functions:
- Four nodal interpolation functions
- Exactly same as the functions for four noded quadrilateral element
1
1   1   ,  2  1 1   1   ,
4
4
1
1
 1  1   1   ,  4  1   1   
4
4
1 
Hierarchic Shape Functions: Rectangular Elements
• Side Nodes Interpolation functions:
- There are 4 p  1 interpolation functions associated with the sides of finite
elements with the order of approximation p  2
- For Side 1
- For Side 2
- For Side 3
- For Side 4
1
1   i  
2
i  2,  , p
2 
1
 1   i  
2
i  2,  , p
3 
1
 1   i  
2
i  2,  , p
1
1   i  
2
i  2,  , p
 i1 
i
i
 i4  
Hierarchic Shape Functions: Rectangular Elements
• Internal Nodes Interpolation functions:
- There are  p  2 p  3 2 interpolation functions associated with the internal
nodes of finite elements with the order of approximation p  4
 0
1
 0
 2   2   ,  2  3  2   ,
 0
 0
 0
 0
 3  2   3   ,  4  4   2   ,
 5  3   3   ,  6  2  4   ,
and so on.
Hierarchic Shape Functions: Rectangular Elements
where, polynomial of degree j is:
 j   
2 j 1
2


Pj 1  t  dt , j  2,3,
1
Pj - is Legendre polynomial.
Using the properties of Legendre polynomials
 j   
1
2  2 j  1
 Pj    Pj 2   
Hierarchic Shape Functions: Rectangular Elements
Legendre polynomial is given by Bonnet Recursion formula:
 n  1 Pn1     2n  1 Pn    nPn1   ,
with P0    1, P1    
and
 2

Pi   Pj   d    2i  1

1
0
1

for i  j
for i  j
n  1, 2,
Hierarchic Shape Functions: Rectangular Elements
Hierarchic Interpolation Functions
For Triangular Element
Hierarchic Shape Functions: Rectangular Elements
• Nodal Interpolation functions:
- Three nodal interpolation functions - L1 , L2 , L3
- Exactly same as the functions for three noded triangular element
• Side Modes:
- There are 3 p  1 side modes and vanish on the other two sides
1
Sides 1:
 i  L2 L1i  L2  L1  ,
where,
1
 j    1   2  j   ,
4


i  2,
j  2,
,p
,p
Hierarchic Shape Functions: Rectangular Elements
For example:

• Internal Modes:
- There are  p  1 p  2  2 internal modes
Mode 1:
 0
1  L1L2 L3
Other modes:
 0
 0
 2  L1L2 L3 P1  L2  L1  ,  3  L1L2 L3 P1  2L3  1
and so on.

7
2
2     6,3     10 ,4    
5  1
8
Physical to Master Element Mapping
Mapping:
• Non rectangular domains cannot be represented using rectangular elements.
However, it can be represented more accurately by quadrilateral elements.
• Interpolation functions are easily available for a rectangular element
• And it is easy to evaluate integral over rectangular geometric
• Therefore, we transform the finite element integral statement over
quadrilaterals to a rectangular.
• Similarly, the finite element integral statement over a triangular element is
transformed to an isosceles triangle.
• Caution: Transformation is for numerical integration purpose only ! The actual
domain is not mapped to another domain.
Mapping:
• Then numerical integration schemes like Gauss-Legendre are used to evaluate
the integrals.
• These schemes require that the integral be evaluated on a specific domain or
with respect to a specific coordinate system.
• In general it is a coordinate system  ,  such that  1   ,  1
• Transformation between physical element  e and master element ̂
m
x

j 1
xejˆ ej  , , y 
m

j 1
y ejˆ ej  , 
e
ˆ

where, j interpolation functions over master element ̂
Mapping:
In general, the dependent variables(s) are approximated by expressions of the
form
u  x, y  
n

u ej ie  x, y 
j 1
The degree of approximations used for the geometry and the dependent
variables(s) are different.
Depending upon it, the finite element formulations are classified as:
- Sub-parametric
- Iso-parametric
- Super parametric
Mapping:


a) super- parametric m  n : The approximation used for the geometry is of
higher order than used for the dependent variable (s).

b) iso-parametric m  n
dependent variable(s).

: Equal degree of approximation for geometry and
- This is extensively used in h- version of finite element programs.
Mapping:
c) Sub-parametric m  n : Approximation order used for geometry is
lower than that used for primary variable (s).
• Coordinate transformations is only for the purpose of numerical
integration.
• When an element is transformed to its master element for the
purpose of numerical integration, the integrand must also be
expressed in terms of the coordinates  ,  of the master element.
Mapping :
For example, consider the stiffness coefficient
e  e
e  e






j
j
e
e
e
i
i
kij   a  x, y 
 b ( x, y )
 c ( x, y ) i  j dxdy
x x
y y

e 



Here, we need to relate
 ie  ie
,
x
y
with
 ie

and
 ie

using the transformation.
• ie ( x, y) can be expressed in terms of local coordinate  and . Hence, the chain
rule for partial differentiation gives
 ie
 ie x
 ie y



x 
y 
In matrix form,
  ie

 

e
  i
 








 x
 

 x
 

y    ie

   x

y    ie
 

 
Jacobian Matrix







 ie
 ie x
 ie y



x 
y 
Mapping :
In matrix form,
  ie

 

e
  i
 








 x
 

 x
 

y    ie

   x

y    ie
 

 







where, the Jacobian matrix is given as
 x
 
 J    x

 

y 
 

y 
 

e
Mapping :
e
e
We need to relate  i ,  i with ˆ ie
x
ˆ ie
and


y
Hence, we need the inverse of the Jacobian matrix.
J  must be non singular.
  ie

 x

e



i

 y
 ˆ ie



1  

  J  
e
ˆ




i

 









Now, using the transformation, we can write
x


x


ˆ ej
m
x
j
j 1
ˆ ej
m
x
j 1

j

,
,
y


y


m

j 1
m

j 1
ˆ ie
yj
,

ˆ ie
yj

Mapping :
 m
 xj
 j 1
J    m

 xj
 j 1
ˆ ie 
 ˆ1
yj

 
 
j 1


m
 ˆ1
ˆ ie 
 
yj




j 1


ˆ ie



ˆ ie


m
ˆ 2

ˆ 2

ˆ m

ˆ m

  x1
 x
 2


  xm
y1 
y2 


ym 
A necessary and sufficient condition for J 1to exist is that the determinant J,
called the Jacobian, be non negative at every point  ,  in ̂ .
x y x y
J  det  J  

0
   
Thus, the function    ( x, y ),   ( x, y ) must be continuous, differentiable
and invertible.
Mapping :
• In case of higher order triangular and rectangular elements the placement of
edge and interior nodes is restricted.
• It can be shown that the side nodes should be placed at a distance greater than
a quarter of the length of the side form either corner node.
x    4(a  1 2)
y    4(b  1 2)

 0,1
 0
6
5
1
4
 0,0
 0
2
1,0
0.25
3
   1
3
y

6
5
1
4
J  1  2  2b  1   2  2a  1  0
 a, b 
0.25
2
x
Mapping :
Mapping the elemental area dA from x,y to d d
  ˆ
dA  dx  dy   dx dy   k


  x
  y
x
y
ˆ
ˆ
ˆ
   d i 
d j    d i 
d


  
  
We have

ˆj    kˆ

 
 x y y y 


d d

     
 J d d
Now, the derivatives of the shape functions with respect to x,y can be given as
  ie

 x

e
  i

 y
 ˆ ie



1  


J
   
e

 ˆ i

 



 ˆ ie


  *   
  J  
e

 ˆ i

 









Mapping :
Now, using this we can write the element calculations over master element as
kije
  i  j

 i  j
 a
b
 c i j dxdy
x x
y y

e 


ˆ
ˆ
   ˆ i
 ˆ i     j
  j 
  aˆ  J11
 J12
 J12

  J11

  

 



ˆ



   i
  i    i
  i 
ˆ
b  J 21
 J 22
 J 22
 J 21
  cˆ i j  J d  d

 

 


or
kije 
 F  ,  d d
ˆ

Mapping of Physical Elements to Master Elements
Affine Mapping
Physical to Master Element Mapping: Linear Triangular Element

3
3
j 1
j 1
x   x jˆ ej , y   y jˆ ej
 0,1
3
 0
   1
y
3
1
2
1
 0,0
2
 0
1,0

Linear Master Element
x
Linear Physical Element
• The affine mapping essentially stretches, translates, and rotates the triangle.
• Straight or planar faces of the reference cell are therefore mapped onto straight
or planar faces in the physical coordinate system.
• Preferred when all the edges of an element are straight.
Numerical Integration: Triangular Element
For three noded triangular element the transformation of co-ordinates is given by
3
x
 x ˆ  , ,
i
i 1
i
3
y
 y ˆ  , 
i
i
i 1
• where, ˆ i are the interpolation functions over the master three noded
triangular element.
ˆ1  1    
ˆ 2  
ˆ 3  
• Master triangle is an isosceles triangle with unit length and right angle
Mapping: Triangular Element
The Jacobian matrix, [J] for the linear triangular element is
 x2  x1
J   
 x3  x1
y2  y1 

y3  y1 
Inverse transformation from the element  e to ̂ is:
1
 x  x1   y3  y1    y  y1   x3  x1  

2A
1
 x  x1  y1  y2    y  y1  x2  x1  

2A
e

where, A the area of the element
Physical to Master Element Mapping: Linear Rectangular Element
y

 1,1
4
1,1
3
3
2
4

1
1
1,1
2
x
1,1
Linear Master Element
Linear Physical Element
4
4
j 1
j 1
x   x jˆ ej , y   y jˆ ej
Mapping of Physical Elements to Master Elements
Iso-parametric Mapping
Physical to Master Element Mapping: Quadratic Triangular Element
6
6
x   x jˆ ej , y   y jˆ ej

j 1
 0,1
y
j 1
3
 0
6
1
 0,0
6
   1
3
5
4
 0
5
1
4
2
1,0

Quadratic Master Element
2
x
Quadratic Physical Element
• The straight faces of the reference triangle are mapped onto curved faces of
parabolic shape in the physical coordinate system.
Physical to Master Element Mapping: Quadratic Rectangular Element

 1,1
4
y
1,1
8
8
3
7
3
2
4
6
1
1,1
7
5

5
6
1
2
x
1,1
Quadratic Master Element
Quadratic Physical Element
8
8
j 1
j 1
x   x jˆ ej , y   y jˆ ej
Mapping of Physical Elements to Master Elements
Blending Function Mapping
Physical to Master Element Mapping: Quadratic Rectangular Element
Curved Quadratic Physical Element with
Side 2 is the only curved side.
x  x2  
y
y  y2  
3
Curve x  x2   , y  y2   given in parametric
form so that
x2  1  X 2 , y2  1  Y2 , x2 1  X 3 , y2 1  Y3
 X i ,Yi  are the coordinates of node i
2
4
1
x
Physical to Master Element Mapping: Quadratic Rectangular Element
We have
1
1
1
1
1


1


X

1


1


X

1


1


X

   1    2    3 1   1    X 4
4
4
4
4
1 
1 

1 
  x2   
X2 
X3 
2
2

 2
x
The first four terms are the linear mapping terms.
The fifth term is the product of two functions:
The bracketed term represents the difference between x2  
and the x-coordinates of the chord that connects  X 2 , Y2  and  X 3 , Y3 
The other is the linear blending function 1    2 , which is unity along side 2 and
zero along side 4.
Physical to Master Element Mapping: Quadratic Rectangular Element
Therefore, we simplify as
1
1
1 
x  1   1    X 1  1   1    X 4  x2  
4
4
2
Similarly,
1
1
1 
y  1   1    Y1  1   1    Y4  y2  
4
4
2
In the general case all sides may be curved. We write the curved sides in the
parametric form:
x  xi   , y  yi   ,  1    1  i  1,2,3,4
Mapping functions are:
1
1
1
1
x   1   1    X1  1   1    X 2  1   1    X 3  1   1    X 4
4
4
4
4
1 
1 
1
1 

x1   
x2   
x3   
x4  
2
2
2
2
Physical to Master Element Mapping: Quadratic Rectangular Element
Mapping functions for y coordinate are:
1
1
1
1
y   1   1    Y1  1   1    Y2  1   1    Y3  1   1    Y4
4
4
4
4
1 
1 
1
1 

y1   
y2   
y3   
y4  
2
2
2
2
Inverse mapping cannot be given explicitly.
Newton-Raphson method or similar procedure is used.
One can see the quadratic iso-parametric mapping as a special application of the
blending function method.
Numerical Integration over a
Master Rectangular Element
Numerical Integration:
kije 
 F  ,  d d
ˆ

1 
1

F  ,  d d   F  ,  d d  



ˆ
1  1
1 



1
 
M
   , 
j
j 1

w j  d

  F  i , j wi w j
M,N - Number of quaddrature points in  and
i ,i  - Gauss points,
wi , w j - corresponding weights.
M
N
i 1
j 1
 directions.
The M  N Gauss point locations are given by the tensor product of one
dimensional Gauss points.
Numerical Integration: Rectangular Element
Selection of integration order
and location of the Gauss
points:
Numerical Integration over a
Master Triangular Element
Numerical Integration:
kije 
 F  ,  d d
ˆ

 NINT

F  ,  dd  
 j , j w j 
 j 1

0
1 1
 F  ,  d d  
ˆ

0
NINT – Number of quadrature points
i ,i  - Gauss points,
wi - corresponding weight.


Numerical Integration: Triangular Element
Numerical Integration: Using Area Co-ordinates
Line integration:
b
L 
m
1
 L2 
k
a
m !k !
ds 
b  a 
 m  k  1!
Area integration:
A  L1 
m
 L2   L2 
k
l
m ! k !l !
dA 
2A
 m  k  l  2 !
Transformation of the co-ordinates to natural co-ordinates:
n
x
x L ,
i i
i 1
where,
n
y
y L
i i
i 1
 xi , yi  are the global coordinates of ith node.
Thank you.
Physical to Master Element Mapping: Quadratic Rectangular Element

 1,1
7
y
1,1
8
8
3
9
2
4
4
1
1,1
5
6
2
7

5
6
1
3
1,1
x
Quadratic Master Element
Quadratic Physical Element
8
8
j 1
j 1
x   x jˆ ej , y   y jˆ ej
• This is also an Iso-parametric mapping of quadratic element.
Physical to Master Element Mapping: Quadratic Triangular Element
y

 0,1
3
6
   1
3
 0
6
5
1
4
 0,0
 0
1
4
5
2
2
1,0
x

Quadratic Master Element
Quadratic Physical Element
• This is also an Iso-parametric mapping of quadratic element.
6
6
j 1
j 1
x   x jˆ ej , y   y jˆ ej