Download Measuring the US Economy

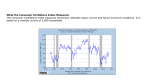
FIN 30220:
Macroeconomics
Measuring the US Economy
The Bureau of Economic Analysis (BEA) reports Gross
Domestic Product (GDP) for the United States on a
quarterly basis:
For the first quarter of 2017, GDP in the United
States was (on an annualized basis) was...
$19,027,000,000,000.00
* Source: www.bea.gov
GDP is the standard benchmark for economic well being. Is it a good indicator of well being?
VS
Ratio
1950: $275B
80
70
60
50
40
30
20
10
0
2016: $18,675B
GDP
1950: $2,200B
1950: $15,000
1950: $16,000
2016: $16,727B
2016: $51,549
2016: $30,240
Real GDP
2009
Dollars
Real Per Capita
GDP
2009 Dollars
Real Median
Income
2015 Dollars
GDP is the standard benchmark for
economic well being. Is it a good indicator
of well being?
VS
Annual defense spending has grown from $35B in
1950 to $732 B in 2017. Should this be subtracted
out?
The service industry has grown from 28M employees in
1950 to 126 M in 2017. Is this really “new activity”?
Should we count things like pollution as
economic “bads”? How do we account for the
added quality and convenience of new products
and technologies?
The Genuine progress indicator, or GPI, is a metric that has been
suggested to replace, or supplement, gross domestic product (GDP) as a
measure of economic growth. GPI is designed to take fuller account of the
health of a nation's economy by incorporating environmental and social
factors which are not measured by GDP.
*Source: Rethinking Progress
The Satisfaction with Life Index was created by Adrian G. White, an analytic social psychologist at
the University of Leicester, using data from a metastudy. It is an attempt to show life satisfaction in
different nations.
Denmark
273
(#1)
143
(#167)
237
(#41)
246.7
(#23)
206
(#90)
210
(#82)
230
(#51)
180
(#152)
210
(#81)
243
(#26)
100
(#170)
Burundi
Note: North Korea Didn’t Participate
In another study, called “The Joy Index”, we have
the following results:
Country Ranking
Joy Index Score (Perfect Score = 100)
#1: China
100
#2 North Korea
98
#3 Cuba
93
#4 Iran
88
#5 Venezuela
85
#152 South Korea
18
#203 (Last Place) United States
3
*The Joy Index was constructed by “researchers” from North
Korea's Chosun Central Television Station.
To understand how to measure GDP, we need to understand the US economy. We need to visualize how goods, services, and
payments flow between sectors of the economy.
Households supply labor and capital to firms
Factor Markets
Firms
Households
Product Markets
Firms supply households with final goods
The Basic circular flow – real goods and services
Every flow of real goods and services is
matched by an equal flow of payments in the
opposite direction
Firms pay wages, interest, profits
Factor Markets
Households supply labor and
capital to firms
Firms
Firms supply households
with final goods
Product Markets
Households Pay for goods and services
Households
Let’s leave out the flow of real goods for simplicity…the basic circular flow is payments from households to firms (payment
for final goods and services) and from firms to households (payment for factor services). However, keep in mind that there
has to be an equal flow in the opposite direction of real goods and services.
Factor
Markets
Households
Firms
Product
Markets
Borrowing and
stock issues by
firms
Now, we can add the financial sector (acting as a
middleman between businesses and firms)
Financial
Markets
Net
Household
savings
Factor
Markets
Households
Firms
Investment
spending
Product
Markets
Now, add the public sector
Financial
Markets
Government
Borrowing
Factor
Markets
Taxes
Households Transfers
Firms
Product
Markets
Government
Spending
Government
Now, add rest of the
world
Financial
Markets
Foreign
Borrowing
Foreign
Lending
Factor
Markets
Households
Firms
Product
Markets
Government
Rest of World
Exports
Imports
Let’s begin by valuing production. We are calculating GDP, so we only need to
worry about production taking place in the United States.
Biggest Issue: Double Counting
Firm A produces raw cotton and sells it to firm B for $1,000
Firms
Production
(GDP)
Product
Markets
Firm B coverts the raw cotton to yarn and sells
it to firm C for $1,500
Firm C coverts the yarn into sweaters
and sells them to the consumer for
$2,500
$1,000 + $1,500 + $2,500 = $5,000
Is there really $5,000 worth of
production? Of course not!
Option #1: Avoid Double Counting By Measuring Value
Value Added
Firm A produces raw cotton and sells it
to firm B for $1,000
$1,000
(Not really, but we need to start somewhere!)
Firm B coverts the raw cotton to yarn
and sells it to firm C for $1,500
Firm C coverts the yarn into sweaters and
sells them to the consumer for $2,500
$500
+ $1,000
$2,500
Example:
GDP Calculation
(Value Added)
Suppose that Intel
produces 1,000 computer
chips (P = $100)
1000 Chips
sold to Dell
1,000 computer
chips @ $100
$100,000
1,000 computers
@ $2,000
$2,000,000
Materials
Expense
GDP
Dell produces 1000
computers (P = $2,000)
- $100,000
$2,000,000
Example with Inventories
GDP Calculation
(Value Added)
Suppose that Intel
produces 1,000 computer
chips (P = $100)
1,000 computer
chips @ $100
$100,000
500 computers
@ $2,000
$1,000,000
1000 Chips
sold to Dell
Materials
Expense
Inventory
Investment
Dell produces 500
computers (P = $2,000)
Dell has 500 chips
remaining in inventories
GDP
- $100,000
$50,000
$1,050,000
Example with capital equipment
GDP Calculation
(Value Added)
Suppose that Xerox
produces 50 copiers
(P = $5000)
50 copiers
@ $5000
$250,000
50 Copiers
sold to Dell
1,000 computers
@ $2,000
$2,000,000
Equipment
expense
- $250,000
Equipment
Investment
$250,000
Dell produces 1000
computers (P = $2,000)
GDP
$2,250,000
GDP Calculation
GDP
1,500 computer
chips @ $100
$150,000
50 copiers
@ $5000
$250,000
1,000 computers
@ $2,000
$2,000,000
Material Expenses
- $355,000
Equipment
Investment
$225,000
Inventory
Investment
$30,000
$2,300,000
Note: This is the full value of the equipment
purchased. If I used the depreciated value, I
would be calculating Net Domestic Product
(Let’s Assume 10% depreciation)
GDP
Depreciation
NDP
$2,300,000
-$22,500
$2,277,500
In July 2013, the BEA announced a change in methodology…
Expenditures for research and development (R&D) and for entertainment, literary,
and artistic originals have many of the characteristics of other fixed assets….
Thus, expenditures on the production of these types of intangible assets, or
intellectual property, be treated as fixed investment.
GDP figures were revised to take into account the new treatment all the way back to 1929
Real Gross Domestic Product.
The revision added
approximately $800B to
GDP in 2017.
All together…
Suppose that
Intel produces
1,500 computer
chips (P = $100)
200 Chips
bought by
households
GDP Calculation
Suppose that Xerox
produces 50 copiers
(P = $5000)
1,300 Chips Bought by Dell
45 Copiers Bought by Dell
Dell Produces 1,000 Computers
(P = $2,000) – sold to consumers
Leaves 300 Chips in inventories
5 Copiers
bought by
households
GDP
1,500 computer
chips @ $100
$150,000
50 copiers
@ $5000
$250,000
1,000 computers
@ $2,000
$2,000,000
Material Expenses
- $355,000
Equipment
Investment
$225,000
Inventory
Investment
$30,000
$2,300,000
Gross Value Added By Sector: 2017Q1
Category
Business
Households & Institutions
Government
GDP
Amount (B)
$14,350
$2,430
$2,247*
$19,027
% of Total
75%
13%
12%
100%
*Equals compensation of general government employees plus general government consumption
of fixed capital.
Option #2: Avoid Double Counting By Measuring Expenditures of End User
Purchases
Firm A produces raw cotton and sells it
to firm B for $1,000
$0
(Not really, but we need to start somewhere!)
Firm B coverts the raw cotton to yarn
and sells it to firm C for $1,500
Firm C coverts the yarn into sweaters and
sells them to the consumer for $2,500
$0
+ $2,500
$2,500
Each good or service produced must be matched by an equal
expenditure
Households
Firms
Government
Product
Markets
Exports
GDP  C  I  G  NX
G
Rest of World
Imports
EX  IM
Let’s recalculate using expenditures
Suppose that
Intel produces
1,500 computer
chips (P = $100)
GDP Calculation
Suppose that Xerox
produces 50 copiers
(P = $5000)
Equipment
Investment
$225,000
Inventory
Investment
$30,000
1,000
Computers
@ $2,000
200 Chips
bought by
households
1,300 Chips Bought by Dell
45 Copiers Bought by Dell
Dell Produces 1,000 Computers
(P = $2,000) – sold to consumers
Leaves 300 Chips in inventories
5 Copiers
bought by
households
GDP
$2,000,000
200 Chips
@$100
$20,000
5 Copiers
@$5,000
$25,000
$2,300,000
The GDP report comes out during the last week of every month
and gives a breakdown by expenditure category
GDP: 2017Q1
Category
Amount (B) % of Total
Consumption
$13,108
69%
Gross Investment
$3,149
17%
Government
$3,328
17%
Net Exports
GDP
-$558
$19,027
-3%
100%
GDP: 2017Q1
Consumption
Expenditures
Goods
GDP  C  I  G  NX
G
$13,108B
$4,219B
Investment Expenditures
Fixed Investment
$3,149B
$3,147B
Durable
$1,439B
Non-Residential
$2,396B
Non-Durable
$2,780B
Structures
$537B
$8,889B
Equipment
$1,074B
Services
Intellectual Property
Let’s take a closer look
at consumption and
investment
Residential
Change in Inventories
$785B
$751B
$2B
We can use this identity to “decompose” economic growth
GDP  C  I  G  EX  IM
G
 IG 
 C 
 G 
 EX 
 IM 
G


%GDP  
%

C

%

I

%

G

%

EX







%IM


 GDP 
 GDP 
 GDP 
 GDP 
 GDP 
Category
2017Q1
% of Total
Growth
(Real)
Contribution to
Real GDP Growth
Consumption
$13,108
69%
0.6%
.44%
Gross Investment
$3,149
17%
4.8%
.79%
Government
$3,328
17%
-1.1%
-.19%
Net Exports
-$558
-3%
---
.13%
Exports
$2,314
12%
5.8%
.70
Imports
$2,872
15%
3.8%
.57
$19,027
100%
GDP
1.2%
GDP: 2017Q1
GDP  C  I  G  NX
G
Real Growth
Consumption
Expenditures
Goods
0.6%
0.3%
Real Growth
Investment Expenditures
Fixed Investment
4.8%
11.9%
Durable
-1.4%
Non-Residential
11.4%
Non-Durable
1.2%
Structures
28.4%
0.8%
Equipment
7.2%
Intellectual Property
6.7%
Services
Let’s take a closer look
at consumption and
investment
Residential
Change in Inventories
13.8%
$4.3B
GDP: 2017Q1
Consumption
Expenditures
GDP  C  I  G  NX
G
Contribution to
GDP Growth
Investment Expenditures
Contribution to GDP
Growth
0.07%
Non-Residential
1.35%
Durable
-0.11%
Structures
0.69%
Non-Durable
0.18%
Equipment
0.39%
0.37%
Intellectual Property
0.27%
Goods
Services
Total
0.44%
Let’s take a closer look
at consumption and
investment
Residential
0.50%
Change in Inventories
-1.07%
Total
0.78%
Option #3: Avoid Double Counting By Measuring Income Earned
Income Earned
Firm A produces raw cotton and sells it
to firm B for $1,000. Profits are $1,000
• $600 Paid to Workers
• $400 Paid to Owners
Firm B coverts the raw cotton to yarn
and sells it to firm C for $1,500. Profits
are $500
• $200 Paid to Workers
• $300 Paid to Owners
Firm C coverts the yarn into sweaters and
sells them to the consumer for $2,500.
Profits are $1,000
• $800 Paid to workers
• $200 Paid to owners
$1,000
(Not really, but we need to start somewhere!)
$500
+ $1,000
$2,500
GDP Calculation
Suppose that
Intel produces
1,500 computer
chips (P = $100)
Wages: $50,000
Suppose that Xerox
produces 50 copiers
(P = $5000)
$150,000
Profits: $100,000
Wages: $200,000
$250,000
Profits: $50,000
Wages: $900,000
200 Chips
bought by
households
1,300 Chips Bought by Dell
45 Copiers Bought by Dell
Dell Produces 1,000 Computers
(P = $2,000) – sold to consumers
Leaves 300 Chips in inventories
$1,900,000
Profits: $1,000,000
5 Copiers
bought by
households
GDP
$2,300,000
To get to income earned by Americans, we need to
account for American production taking place abroad
and foreign production within the US
Nike began manufacturing sport
shoes and apparel in Thailand in
1980. Currently Nike has 84
contract factories employing
75,000 people and producing
$500M annually.
In 1992, BMW built a
production facility in
Spartanburg, South Carolina – it
employs 10,000 people and
produced 297,326 units in 2013
(approx. $13B).
Gross Domestic Product vs. Gross National Product
Nike
• Sales: $500M
• Value Added: $200M
 $50M Paid to Foreign labor
 $10M paid to American labor
 $40M paid to foreign investors
 $100M paid to American investors
BMW
• Sales: $13B
• Value Added: $5B
 $3B paid to American labor
 $1B paid to Foreign labor
 $400M paid to US investors
 $600M Paid to foreign investors
GDP
GDP
$5B
BMW’s output was produced
inside the US
$0
Nike’s output was produced
outside the US
$5B
Gross Domestic Product vs. Gross National Product
Nike
• Sales: $500M
• Value Added: $200M
 $50M Paid to Foreign labor
 $10M paid to American labor
 $40M paid to foreign investors
 $100M paid to American investors
BMW
• Sales: $13B
• Value Added: $5B
 $3B paid to American labor
 $1B paid to Foreign labor
 $400M paid to US investors
 $600M Paid to foreign investors
$3B
$400M
GNP
$10M
$100M
GNP
$3.51B
Paid as wages to US citizens
Paid as profits to US investors
Paid as wages to US citizens
Paid as profits to US investors
GDP
Alternatively….
GDP
BMW
• Sales: $13B
• Value Added: $5B
 $3B paid to American labor
 $1B paid to Foreign labor
 $400M paid to US investors
 $600M Paid to foreign investors
Nike
• Sales: $500M
• Value Added: $200M
 $50M Paid to Foreign labor
 $10M paid to American labor
 $40M paid to foreign investors
 $100M paid to American investors
+
+
-
BMW’s output was produced
inside the US
$0
Nike’s output was produced
outside the US
$5B
$10M paid to American labor
$100M paid to American investors
$1B paid to Foreign labor
$600M paid to Foreign investors
GNP
GNP = GDP + Net Factor Payments (NFP)
$5B
Income
earned by
Americans
abroad
Income
earned by
foreigners in
the US
$3.51B
Income earned by Foreigners in the US
Income by Americans in the US
Factor
Markets
Income
earned by
Americans
abroad
2017Q1
Households
Firms
NDP
Net Domestic Product = GDP - Depreciation
GDP
+ Net Factor Payments
- Depreciation
- Statistical Discrepancy
National Income
$19,027
$ 237
$ 2,975
-$ 130
$16,419
National Income by Source: 2017Q1
Category
Amount(B) % of Total
Compensation of Employees
$10,267
63%
Proprietor’s Income
$1,458
9%
Rental Income
$736
4%
Corporate Profits
$2,110
13%
Net Interest and Misc.
$481
3%
Indirect Taxes (Sales Tax and Tariffs)
$1,264
Less Subsidies
$59
Labor Share of Income
Capital Share of Income
7%
Surplus of Government Enterprises
-$22
Net Business Transfers
$184
1%
National Income
$16,419
100%
Financial
Markets
Personal Income = Outlays
NI  C  S  T
National
Income
Households
Firms
Product
Markets
Government
Every dollar earned income has to
be spent
Personal Income to Personal Savings: 2017Q1 (Billions)
Personal Income
Less Personal Taxes
Equal Personal Disposable Income
Less Personal Outlays
$16,330
$1,995
$14,335
$13,590
Consumption Expenditures
$13,108
Interest Payments
$284
Personal Transfers
$198
Equals Personal Savings
$747
Personal Savings as % of Disposable Income
5.2%
This number includes healthcare
payments made by
Medicare/Medicaid
SO, this number includes
401k/pension plan contributions
Personal Savings Rate in the US
Side Note
China: 25%
India: 21%
S. Korea: 21%
Thailand: 14%
16
% if Disposable Income
14
12
10
8
6
4
2
0
1960
1965
1970
1975
1980
1985
1990
1995
2000
2005
2010
2015
Let’s apply “Output equals Income” to the GDP equals expenditures identity
GDP  C  I  G  NX
 NFP
 NFP
G
GNP  C  I  G  CA
 DEP
 DEP
N
NI  C  I  G  CA
G
I N  I G  DEP
Output equals expenditures
CA  NX  NFP
Now, let’s apply “Income equals Outlays”
NI  C  I  G  CA
T
T
N
 NI  T   C  I   G  T   CA
C C
N
S  I   G  T   CA
N
Government
Deficit
Flow of Funds
Financial
Markets
Foreign
Borrowing
Lastly, we have an
accounting identity for the
financial markets known as
the flow of funds
Foreign
Lending
Households
Firms
Government
S   I   G  T   CA
Rest of World
N
Also, every dollar that is
saved is borrowed
Gross Savings
Net Savings
$3,390
$445
Domestic Business
$628
Personal Savings
$699
Government Savings
-$883
Consumption of Fixed Capital
GPS  I G  G  T   CA
Net Household Lending
Net Savings: $699
+ Consumption of Fixed Capital: $502
- Gross Investment: $760
$441
$2,945
Net Business Lending
Domestic Business
$1,912
Households
$502
Net Savings: $630
+ Consumption of Fixed Capital: $1,912
- Gross Investment: $2,341
Government
$530
Gross Investment
$201
$3,724
Net Government Lending
Private (Household And Business)
$2,341
Household
$760
Net Savings: -$883
+ Consumption of Fixed Capital: $530
- Gross Investment: $623
Government
$623
-$976
Note: Statistical Discrepancy = -$143
US Current Account Balance
(0.7% of GDP)
$47-B
100
0
1947
1952
1957
1962
1967
1972
1977
1982
1987
1992
1997
2002
2007
2012
Billions of Dollars
-100
-200
-300
-400
-$479B
(-2% of GDP)
-500
-600
-700
-800
-900
-$859B
(-6% of GDP)
We can analyze this using the “Income Equals Outlays” Identity….
CA  NI   C  I  G 
N
Total US Income
We are living beyond our
means!
Total US Spending
Or, we can analyze this using the “Flow of Funds” Identity….
S  I  G  T   CA
G
We are borrowing more that
we are saving!
Public Borrowing
Private Borrowing
Household Saving
In other words, the US is borrowing over $1B per day from abroad! Should we be worried about this?
Personal Savings/Net Lending By Households
1200
* The Difference between personal
savings and net lending by households
is gross investment by households
Billions of Dollars
1000
800
600
400
200
0
1960
1965
1970
1975
1980
1985
1990
1995
-200
-400
Household Net Lending
Personal Savings
2000
2005
2010
2015
Net Lending By Households/Business
1200
1000
Billions of Dollars
800
600
400
200
0
1960
1965
1970
1975
1980
1985
1990
-200
-400
-600
-800
Households
Business
1995
2000
2005
2010
2015
Net Lending By Households/Business/Government
Billions of Dollars
1000
500
0
1960
1965
1970
1975
1980
1985
1990
1995
-500
-1000
CA  S  I  G  T 
G
-1500
-2000
Government
Households
Business
2000
2005
2010
2015
Lets take a look at the US economy from 1947 to 2016 …
20000
$18,860B
(2016Q4)
18000
16000
Billions of Dollars
14000
12000
10000
8000
6000
4000
2000
$243.1B
(1947Q1)
0
1947
1954
1961
1968
1975
1982
Average
Annual
Growth
1989
1996
2003
2010
 ln 18,860   ln  243.1 

 *100  6.31%
69


However, remember the problem we ran into with the movie grosses. GDP (current market value of goods and services
produced) isn’t really the same in 1947 as it is in 2014 because the dollar has lost a lot of its value (i.e. prices have gone up)
1947
Car: $1,500
Gasoline: 23 cents/gal
House: $13,000
Bread: 12 cents/loaf
Milk: 80 cents/gal
Postage Stamp: 3 cents
2017
Car: $33,560
Gasoline: 2.27 dollars/gal
House: $234,000
Bread: $1.98 dollars/loaf
Milk: 3.98 dollars/gal
Postage Stamp: 49 cents
We need to construct a “price index” to represent and average
of prices over a wide variety of products. How do we do this?
The objective of a price index is to measure cost of living. To state this precisely, a price index measures the
dollar cost of obtaining a fixed level of utility (happiness). Suppose at the current prices, you elect to buy 3
slices of pizza and 2 beers
The absolute dollar cost of your current
happiness is (2)($3.50) + (3)($2.00) = $13
Example:
$3.50
$2.00
As prices change, we keep the quantities of each good constant (guaranteeing a constant level of utility)
Good
Base Year
Price (BY)
Base Year
Quantity
Current Year Price
(CY)
Inflation
Beer
$3.50
2
$4.50
25%
Pizza
$2
3
$2.20
10%
(2)($4.50) + (3)($2.20) = $15.60
ln 15.60   ln 13  *100  18%
Alternatively, we could write the price index in terms of relative dollars (relative to a base year) instead of absolute
dollars (this is how its actually calculated).
Good
Base Year
Price (BY)
Base Year
Quantity
Current Year Price
(CY)
Inflation
Beer
$3.50
2
$4.50
25%
Pizza
$2
3
$2.20
10%
Base Year Expenditure: (2)($3.50) + (3)($2.00) = $13
Beer Expenditure Share: (2)($3.50)/$13 =.54
Pizza Expenditure Share: (3)($2)/$13 = .46
 3.50 
 2.00 
PBY  .54  
  .46  
  1.0
3.50
2.00




(Or, 100)
 4.50 
 2.20 
PCY  .54  

.46




  1.2
 3.50 
 2.00 
(Or, 120)
ln 120   ln 100   *100  18%
The CPI is calculated by the Bureau of Labor Statistics (BLS) on a monthly basis
Personal Care
4%
Consumer
Price Index
Tobacco &
Smoking Products
1%
Food & Beverage
16%
Education &
Communication
5%
Housing
40%
Recreation
6%
The CPI is composed of 211
individual products over 38
geographic areas (8,018 total
prices).
Medical
6%
Transportation
17%
Apparel
5%
When Calculating the Consumer Price Index, the expenditure shares remain constant!!!
Good
Base Year Price (1983)
Year 2015 Price
Year 2016 Price
Housing
$200
$780
$800
Transportation
$90
$280
$300
Food
$40
$190
$200
Apparel
$30
$245
$250
 200 
 90 
 40 
 30 
CPI1983  .40  
  .30     .20     .10     1
 200 
 90 
 40 
 30 
Household Budget
( or, 100 )
 780 
 280 
 190 
 245 
CPI 2015  .40  

.30

.20

.10












  4.25
200
90
40
30








Or, 425
 800 
 300 
 200 
 250 
CPI 2016  .40  

.30

.20

.10












  4.43
200
90
40
30








( or, 443 )
Average CPI inflation
 ln  443  ln 100  

 *100  4.50%
33


CPI inflation (2015 – 2016)
  ln  4.43  ln  4.25   *100  4.15%
The Consumer Price Index (1948 – 2016)
16
300
CPI
12
10
250
200
8
6
150
4
100
2
0
1948
-2
1956
1964
1972
1980
1988
-4
2004
2012
50
0
1983 = 100
Average Inflation = 3.54%
1996
CPI
CPI Inflation Rate
14
Note that expenditure shares do change over time, so the weights need to be updated periodically
Expenditure shares in the CPI were last updated in 2013-14
Potential problem #1: Products change over time. Suppose you observe the following TV Prices
2003
2004
Price: $250
Features: 27 inch
Cathode Ray Tube
Enhanced Definition TV
S-Video Input
Universal Remote
Price: $1,250
Features: 42 inch
Plasma
High Definition TV
S-Video Input
Universal Remote
 $1, 250  $250 

 *100  400%
$250


Note: The first plasma TV was released by Fijitsu 1n 1995. The 42’’ TV cost $14,999
Is this a fair
assessment of
inflation?
Solution: Hedonic Price Adjusting
Price: $250
Features: 27 inch
Cathode Ray Tube
Enhanced Definition TV
S-Video Input
Universal Remote
These three featured
are estimated to be
worth $100
Price: $1,250
Features: 42 inch
Plasma
High Definition TV
S-Video Input
Universal Remote
These three featured
are estimated to be
worth $1000
Hedonically Adjusted price = $1,250 – ($1,000 -$100) = $350
Solution: Hedonic Price Adjusting
Around a third of the CPI is Hedonically
Adjusted
Item
Relative
Importance
Men’s Suits, Sport coats and Outerwear
.113
Men’s Shirts and Sweaters
.207
Men’s Pant’s and Shorts
.160
Boy’s Apparel
.188
Women’s Outerwear
.114
Women’s Dresses
.154
Women’s Suits and Separates
.604
Girl’s Apparel
.204
Men’s Footwear
.216
Boy’s and Girl’s Footwear
.169
Educational Books and Supplies
.195
Major Appliances
.159
Televisions
.161
Other Video Equipment
.030
Rent of Primary Residence
29.483
Total = 32.165%
Potential Problem #2: What about housing? Consider the following examples
Option #1: Rent a
$240,000 house
$1,000/mo.
Option #2: Buy a
$240,000 house
with an interest only
mortgage (5% per
year)
$240,000(.05) = $12,000/yr.
= $1,000/mo.
Option #3: Buy a
$240,000 house
with a 30 year
mortgage (5% per
year)
$1,288/mo.
Potential Problem #2: What about housing? Consider the following
examples
Option #3: Buy a
$240,000 house
with a 30 year
mortgage (5% per
year)
Option #1: Rent a
$240,000 house
OR
Option #2: Buy a
$240,000 house
with an interest only
mortgage (5% per
year)
$1,288/mo.
$1,000/mo.
Difference = $288/mo.
What if you put
$288/mo. and put it
in a savings account
that earns 5% per
year?
Potential Problem #2: What about housing? Consider the following examples
Option #1: Rent a
$240,000 house
OR
Option #2: Buy a
$240,000 house
with an interest only
mortgage (5% per
year)
Option #3: Buy a
$240,000 house
with a 30 year
mortgage (5% per
year)
$1,000/mo.
(This is pure cost of living)
$1,288/mo.
(This is cost of living plus investment in an asset)
Solution: In 1983, the BLS decided to focus entirely on rental markets for housing.
Housing Prices
Housing Inflation
400.0
15
350.0
300.0
10
250.0
200.0
5
150.0
0
1976
100.0
50.0
1986
1991
1996
2001
-5
0.0
1976
1981
1981
1986
1991
Home Price Index
Average Inflation Rate
Home Price Index: 4.40%
Rental Index: 4.01%
1996
2001
2006
Rental Price Index
2011
-10
Home Price
Rental Price
Can you spot the housing
bubble?
2006
2011
Potential Problem #3: Substitution
Recall that at the original prices, you elected to
buy 3 slices of pizza and 2 beers
The cost of your happiness at the initial
prices is
$3.50
(2)($3.50) + (3)($2.00) = $13
$2.00
Good
Base Year
Price (BY)
Current Year Price
(CY)
Inflation
Beer
$3.50
$4.50
25%
Pizza
$2
$2.20
10%
(1)($4.50) + (4)($2.20) = $13.30
If beer increases in price to $4.50 (25% increase) and
pizza increases to $2.20 (10% increase), suppose you
alter your decision and buy 1 beer and 4 slices of pizza
ln 13.30   ln 13  *100  2.2%
Original Expenditure:
(2)($3.50) + (3)($2.00) = $13
Good
Base Year
Price (BY)
Current Year Price
(CY)
Inflation
Beer
$3.50
$4.50
25%
Pizza
$2
$2.20
10%
No Substitution:
Substitution:
(2)($4.50) + (3)($2.20) = $15.60
(1)($4.50) + (4)($2.20) = $13.30
ln 15.60   ln 13  *100  18%
ln 13.30   ln 13  *100  2.2%
Which measure of inflation is more realistic?
Solution: In 2000, the BLS introduced a “chain weighted CPI” that allows for this substitution between different
goods. It’s thought to be a better gauge of inflation. Expenditure shares in the Chain CPI are updated every two
years.
6.0
160.000
CCPI
5.0
120.000
3.0
100.000
2.0
80.000
1.0
60.000
0.0
1999
-1.0
2001
2003
2005
2007
2009
2011
2013
2015
40.000
-2.0
20.000
-3.0
0.000
Chained CPI
Inflation Rate
4.0
140.000
It is, however, very controversial…
Average Inflation Rate
CPI: 2.31%
CCPI: 2.06%
6
5
Inflation Rate
4
3
2
1
0
2000
2001
2002
2003
2004
2005
2006
2007
-1
-2
-3
CPI
CCPI
2008
2009
2010
2011
2012
2013
Example: Suppose that you are a social security recipient. Let’s calculate your total payments received in
social security payments under the different inflation measures from 2000 to 2016. (Assume you received
the average social security payment of $1,180 per month in 2000)
CPI Inflation Rate (2.31% per year)
$14,160  $14,160 1.0231  $14,160 1.0231  ...  $14,160 1.0231  $290, 784
2
16
CCPI Inflation Rate (2.06% Per Year)
$14,160  $14,160 1.0206   $14,160 1.0206   ...  $14,160 1.0206   $284, 787
2
16
Difference = $5,997
($352/yr.)
Now, consider that there are
approximately 65 million social security
recipients:
$5,997*65M = $390B
($23B/yr.)
An alternative to the consumer price index is the GDP Deflator.
Suppose we have the following Data
Good
Production (2014)
Current Price (2014)
Current Value
Housing
300
$550
$165,000
Transportation
500
$350
$175,000
Food
100
$260
$26,000
Apparel
200
$220
$44,000
Total = GDP (Current Dollars)
$410,000
Now, Suppose we revalue current GDP at, say, prices in 2009 (Call this the base year)
Good
Production (2014)
2009 Price
2009 Value
Housing
300
$500
$150,000
Transportation
500
$300
$150,000
Food
100
$200
$20,000
Apparel
200
$200
$40,000
Total = GDP (2009 Dollars)
$360,000
We can use these two numbers to construct an implied relative price
Current value of current
production (2014)
Base year value of current
production (Base year = 2009)
$410,000 (Current Dollars)
$360,000 (2009 Dollars)
$410,000 (Current Dollars)
$360,000 (2009 Dollars)
Note that the base year (2009) is 1 (or, 100) by definition
 ln 114   ln 100  

 *100  2.62%
5


= 1.14 (or, 114)
It turns out that the deflator is still a weighted average of individual relative prices
Good
Production (2014)
2009 Price
2009 Value
2014 Price
Housing
300
$500
$150,000
$550
Transportation
500
$300
$150,000
$350
Food
100
$200
$20,000
$260
Apparel
200
$200
$40,000
$220
Total = GDP (2009 Prices)
Housing Share of Real GDP
 $150, 000 
 $360, 000   .41


$360,000
Transp. Share of Real GDP
 $150, 000 
 $360, 000   .41


Food Share of Real GDP
 $20, 000 
 $360, 000   .06


Apparel Share of Real GDP
 $40, 000 
 $360, 000   .12


With the implied weights, you can calculate the GDP deflator in a similar fashion as the CPI
 $550 
 $350 
 $260 
 $220 
P  .41

.41

.06

.12






  1.14
 $500 
 $300 
 $200 
 $200 
(Or, 114)
Suppose we repeat for a different year to calculate an inflation rate
Good
Production (2013)
2009 Price
2013 Price
Housing
280
$500
$535
Transportation
490
$300
$310
Food
105
$200
$240
Apparel
170
$200
Value of GDP at
2013 Prices
$363,620
$342,000
$216
= 1.06 (or, 106)
Value of GDP at
2009 Prices
Housing Share of Real GDP
 $140, 000 
 $342, 000   .41


Transp. Share of Real GDP
 $147, 000 
 $342, 000   .43


Food Share of Real GDP
 $21, 000 
 $342, 000   .06


Apparel Share of Real GDP
 $34, 000 
 $342, 000   .10


 $535 
 $310 
 $240 
 $216 
P  .41

.43

.06

.10






  1.06
 $500 
 $300 
 $200 
 $200 
Index Inflation
ln 114   ln 106   *100  7.27%
(Or, 106)
Now, the inflation rate incorporates price changes as well as expenditure share changes – a lot like the chained
CPI!
Good
2013 Price
2014 Price
Inflation
Housing
$535
$550
2.76%
Transportation
$310
$350
12.10%
Food
$240
$260
8.00%
Apparel
$216
$220
1.83%
2013
Housing Share of Real GDP
 $140, 000 
 $342, 000   .41


Transp. Share of Real GDP
 $147, 000 
 $342, 000   .43


Food Share of Real GDP
 $21, 000 
 $342, 000   .06


Apparel Share of Real GDP
 $34, 000 
 $342, 000   .10


2014
Housing Share of Real GDP
 $150, 000 
 $360, 000   .41


Transp. Share of Real GDP
 $150, 000 
 $360, 000   .41


Food Share of Real GDP
 $20, 000 
 $360, 000   .06


Apparel Share of Real GDP
 $40, 000 
 $360, 000   .12


Average Inflation: 3.20%
The GDP Deflator: 1948 - 2014
12
120
GDP Def.
10
100
80
6
4
60
2
40
0
1948
-2
-4
1960
1972
1984
1996
2008
20
2009 = 100
0
GDP Deflator
Inflation Rate
8
A comparison between the CPI (Fixed Weight Index) and the GDP Deflator (Variable
Weight Index)
Good
Production (2000)
Price (2000)
Production (2015)
Price (2015)
Apples
350
$25
400
$30
Oranges
250
$50
600
$55
Note the large expansion of the orange industry
Inflation Rate For Apples
ln  $30   ln  $25   *100  18.2%
Inflation Rate For Oranges
ln  $55   ln  $50   *100  9.5%
Any price index should produce an inflation rate between 9.5% and 18.2%
Good
Production (2000)
Price (2000)
Production (2015)
Price (2015)
Apples
350
$25
400
$30
Oranges
250
$50
600
$55
Let’s assume an economy where
there is only a consumption
sector….
GDP  C
(Production shares equal consumption shares)
Let’s make the base year 2000
GDP2000   350  $25    250  $50   $8750  $12,500  $21, 250
Apple expenditure share
A
$8, 750
 .41
$21, 250
Orange expenditure share
O
$12,500
 .59
$21, 250
Base Year Expenditure
Shares
A comparison between the CPI (Fixed Weight Index) and the GDP Deflator (Variable Weight Index)
Good
Production (2000)
Price (2000)
Production (2015)
Price (2015)
Apples
350
$25
400
$30
Oranges
250
$50
600
$55
ln  $30   ln  $25   *100  18.2%
ln  $55   ln  $50   *100  9.5%
Consumer Price Index (CPI)
 $25 
 $50 
CPI 2000  .41 

.59
  
 1
 $25 
 $50 
 $30 
 $55 
CPI 2015  .41 

.59
  
  1.141
 $25 
 $50 
Remember…the expenditure shares are held
constant at the base year’s expenditure shares
CPI Inflation Rate
ln 1.141  ln 1  *100  13.2%
Good
Production (2000)
Price (2000)
Production (2015)
Price (2015)
Apples
350
$25
400
$30
Oranges
250
$50
600
$55
GDP Deflator (DEF)
GDP2000   350  $25    250  $50   $8750  $12,500  $21, 250
RGDP2000   350  $25    250  $50   $8750  $12,500  $21, 250
 $21, 250 
DEF2000  
1

 $21, 250 
GDP2015   400  $30    600  $55   $12, 000  $33, 000  $45, 000
RGDP2015   400  $25    600  $50   $10, 000  $30, 000  $40, 000
 $45, 000 
DEF2015  
 1.125

 $40, 000 
GDP Deflator Inflation Rate
ln 1.125   ln 1  *100  11.8%
Good
Production (2000)
Price (2000)
Production (2015)
Price (2015)
Apples
350
$25
400
$30
Oranges
250
$50
600
$55
Inflation Rate For Apples
Inflation Rate For Oranges
ln  $30   ln  $25   *100  18.2%
ln  $55   ln  $50   *100  9.5%
CPI Inflation Rate
GDP Deflator Inflation Rate
ln 1.141  ln 1  *100  13.2%
ln 1.125   ln 1  *100  11.8%
Why the discrepancy?
Good
Production (2000)
Price (2000)
Production (2015)
Price (2015)
Apples
350
$25
400
$30
Oranges
250
$50
600
$55
GDP Deflator (DEF) Implied Weights
RGDP2000   350  $25    250  $50   $8750  $12,500  $21, 250
A2000
 $8, 750 

  .41
$21,
250


A2000
 $12,500 

  .59
$21,
250


 $25 
 $50 
DEF2000  .41 

.59
  
 1
 $25 
 $50 
RGDP2015   400  $25    600  $50   $10, 000  $30, 000  $40, 000
 $10, 000 
A2015  
  .25
$40,
000


 $30, 000 
O2015  
  .75
$40,
000


 $30 
 $55 
DEF2015  .25  

.75
  
  1.125
 $25 
 $50 
The GDP deflator is a variable weight index…the
weights (which are actually production shares)
fluctuate!!
Good
Production (2000)
Price (2000)
Production (2015)
Price (2015)
Apples
350
$25
400
$30
Oranges
250
$50
600
$55
Inflation Rate For Apples
Inflation Rate For Oranges
ln  $30   ln  $25   *100  18.2%
ln  $55   ln  $50   *100  9.5%
CPI Inflation Rate
ln 1.141  ln 1  *100  13.2%
GDP Deflator Inflation Rate
ln 1.125   ln 1  *100  11.8%
A2000  .41
A2000  .59
A2000  .41
A2000  .59
A2015  .41
A2015  .59
A2015  .25
A2015  .75
As oranges production grows relative to apples (most likely because they are becoming relatively cheaper), the GDP
deflator increases the weight of oranges while the CPI keeps the weight fixed.
Average Inflation
Inflation with the GDP Deflator versus the CPI
CPI: 3.55%
GDP Def.: 3.20%
16
14
12
10
8
6
4
2
0
1948-01-01
1958-01-01
1968-01-01
1978-01-01
1988-01-01
1998-01-01
2008-01-01
-2
Let’s enlarge this area
-4
CPI
GDP Deflator
Inflation with the GDP Deflator versus the CPI
Average Inflation
What’s going on here?
CPI: 2.30%
GDP Deflator: 2.01%
6
5
4
3
2
1
0
2001
2003
2005
2007
2009
-1
-2
CPI
GDP DEF
2011
2013
6
4
2
0
2001
2003
2005
2007
2009
2011
2013
-2
CPI
GDP DEF
80
60
40
20
0
-20 2001
2003
2005
2007
2009
2011
2013
-40
-60
-80
-100
Oil Price Inflation
Recall that a large portion of our oil is imported and is therefore not a part of GDP.
Which means its not a part of the GDP deflator!
The “core CPI” removes food and energy prices due to their excessive volatility.
Average Inflation
CPI: 2.30%
Chain CPI: 2.06%
GDP Deflator: 2.01%
Core CPI: 1.95%
So, what is inflation in the US currently?
Price Index
Current Value
Annualized
Current Value
Year on Year
CPI (December)
.3% (per month)
3.6%
2.07%
Core CPI (December)
.2% (per month)
2.4%
2.15%
Chained CPI (December)
0.07% (per month)
0.78%
2.02%
PCE Index (December)
.15% (Per Month)
1.8%
1.78%
Implicit GDP Deflator
0.525% (Per quarter) 2.1%
1.65%
AVERAGE
2.12%
So, by current methodologies,
we are around 2% per year.
1.93%
Preferred
measure for the
Fed
Pre 1990 Methodologies = 5.5%
Pre 1990 Methodologies = 2%
But, is inflation really 2%?
Pre 1980 Methodologies = 10%
Current Methodologies = 2%
Source: Shadowstats.com
Lets take a look at the US economy from 1947 to 2017 …
20000
$19,027B
(2017Q1)
18000
16000
Billions of Dollars
14000
12000
10000
8000
6000
4000
2000
$243.1B
(1947Q1)
0
1947
1952
1957
Average
Annual
Growth
1962
1967
1972
1977
1982
1987
1992
1997
2002
 ln 19,027   ln 243.1 

 *100  6.2%
70


2007
2012
2017
Lets use the consumer price index to adjust these nominal values to reflect year 2000 prices
20000
$19,027B
2017Q1
Billions of Dollars
18000
16000
14000
 170.1 
$19,027
  $13,258
 244.1 
12000
10000
8000
6000
4000
$243.1B
(1947Q1)
2000
0
1947
 170.1 
$243.1
  $1,905.6
 21.7 
1954
1961
1968
1975
1982
1989
Average
Annual Real
Growth
1996
2000
2003
2010
2017
 ln 13,258  ln 1,905.6  

 *100  2.7%
70


Now, looking at real GDP over the last 67 years, we should see two basic features in the data
14000
$13,258B
2017Q1
Billions of 2000 Dollars
12000
10000
$1,905.6B
(1947Q1)
1) The US economy grows
over time
2) The US doesn’t grow at a
constant rate
8000
6000
4000
2000
0
1947
1954
1961
1968
1975
1982
1989
1996
2003
2010
2017
Side Note: If we are measuring inflation incorrectly, we are also measuring real GDP
incorrectly
Real GDP Using the Current
GDP Deflator Methodology
Year 2000 = 100
Real GDP Using the Current
GDP Deflator Methodology
Year 2000 = 100
Source: Shadowstats.com
Here’s an exaggerated view of what we are talking about
GDP
“Business Cycle”
(deviations from trend)
Trend (Average growth)
Time
The business cycle is a repeated pattern of recessions
followed by recoveries
Recession
(Below
Trend
Growth)
Recovery
(Above
Trend
Growth)
GDP
Trend (Average growth)
Peak
Peak
Trough
Time
How do we best describe long run growth in the US – Linear Trend
14000
Number of Quarters from 1947Q1
Billions of 2000 Dollars
12000
Trend  41.4 x  973.4
$10,412.6B
10000
The economy
grows by $41.4B
per quarter
8000
6000
4000
2000
973.4
0
1947
1954
1961
1968
1975
1982
1989
1996
2003
2010
2017
2004Q1 (228 Quarters)
Trend  41.4228  973.4  10,412.6
How do we best describe long run growth in the US – Exponential Trend
18000
Number of Quarters from 1947Q1
Billions of 2000 Dollars
16000
14000
12000
Trend  2,236e.0069 x
The economy
grows by .69%
per quarter
10000
8000
6000
4000
2000
973.4
0
1947
1954
1961
1968
1975
1982
1989
1996
2003
2010
2017
2004Q1 (228 Quarters)
Trend  2,236e.0069 228   10,782.1
An exponential trend assumes that the US has some constant annual rate of real economic growth (~3% per
year). Note that actual growth varies even over long time periods.
5
Annual Growth Rate
4
Average Real
Growth = 3%
3
2
Current Real
Growth
1
1950's
1960's
1970's
1980's
1990's
2000's
Actually, it looks like long term growth in the US actually has its own cycle...again, an exponential trend can’t
capture this
6
5
Annual Growth Rate
4
3
2
1
0
The HP trend allows trend growth to vary over time
14000
Billions of 2000 Dollars
12000
10000
8000
6000
4000
2000
$1,938B
(1947Q1)
0
1947 1952 1957 1962 1967 1972 1977 1982 1987 1992 1997 2002 2007 2012
The HP Trend solves this
minimization problem
$12,129B
2014Q1
How do we best describe long run growth in the US – HP Trend
14000
Billions of 2000 Dollars
12000
$10,967.0B
10000
8000
6000
4000
2000
0
1947
The HP Trend
solves this
minimization
problem
1954
1961
1968
1975
1982
1989
1996
2003
2010
2017
2004Q1 (228 Quarters)
Trend  $10,967.0
Once we have identified the trend, we can subtract it out to leave the cycle component all by itself.
GDP
Trend (Average growth)
Trend GDP
 Actual  Trend 
Deviation  
 *100
Trend


Actual GDP
Time
We end up with a series that looks like this
% Deviation
From Trend
Recovery
Recession
Peak
Peak
0
Trough
Time
Once we have identified the trend, we can remove it.
12000
Billions of 2000 Dollars
Actual = $11,849B
11500
Trend = $11,570B
11000
Trend = $10,693B
10500
Actual = $10,417B
10000
9500
2000
2001
2002
2003
2004
2005
10,417  10,693 *100  2.6%
% Deviation 
10,693
2006
2007
% Deviation 
2008
11,849  11,570 *100  2.4%
11,570
Here is the cycle by itself
Economy Growing Faster
than Trend
Economy Growing Slower
than Trend
3
2
1
0
2000
2002
2004
2006
2008
-1
-2
-3
10,417  10,693 *100  2.6%
% Deviation 
10,693
% Deviation 
11,849  11,570 *100  2.4%
11,570
Let’s look at the cycle component for the US
Percentage Deviation from HP Trend
6
4
2
0
1947
1952
1957
1962
1967
1972
1977
1982
1987
1992
1997
2002
2007
2012
-2
-4
-6
-8
1
2
3
4
5
6
7
8
9
10
11
The US has had 11 Cycles since the World War II
The US has had 11 Cycles since the World War II
Business Cycle Dates
Peak
Trough
Duration (In Months)
Contraction
Expansion
Cycle (Peak from
(peak to trough)
(Previous trough to
this peak)
previous peak)
Nov 1948
Oct 1949
11
37
45
July 1953
May 1954
10
45
56
Aug 1957
April 1958
8
39
49
April 1960
Feb 1961
10
24
32
Dec 1969
Nov 1970
11
106
116
Nov 1973
March 1975
16
36
47
Jan 1980
July 1980
6
58
74
July 1981
Nov 1982
16
12
18
July 1990
March 1991
8
92
108
March 2001
Nov 2001
8
120
128
December 2007
June 2009
18
73
81
13
55
68
Average
When we talk
about “business
cycle frequency,
we are referring to
cycles between 2
and 8 yrs.
The US has had 33 Cycles since the Civil War. On averages, in recent years, the recessions are
getting shorter and the recoveries longer
Average (Months)
Recession
(Peak to
Trough)
Expansion (Trough
to peak)
Cycle ( Peak to
Peak)
1854 – 2009 (33 cycles)
17.5
38.7
56.2
1854 – 1919 (16 cycles)
21.6
26.6
48.2
1919 – 1945 (6 cycles)
18.2
35.0
53.2
1945 – 2009 (11 cycles)
11.1
58.4
69.5
When we talk
about “business
cycle frequency,
we are referring to
cycles between 2
and 8 yrs.
It also seems that recently, the business cycle has become less severe in recent years.
Percentage Deviation from Trend
6
4
2
0
1947
1952
1957
1962
1967
1972
1977
1982
1987
1992
1997
2002
2007
-2
-4
-6
-8
1
2
3
4
5
6
7
8
9
10
11
2012
In fact, look at the cycle now relative to the great depression era
30
% Deviation from trend
Industrial Production
20
10
0
1/1/1919
1/1/1939
-10
-20
-30
-40
Great Depression WWII
1/1/1959
1/1/1979
1/1/1999
13900.0
Actual
% Deviation from Trend (Cycle)
13700.0
 13,326  12,994 

 *100  2.5%
12,994


Trend
13500.0
$13,326B
GDP
13300.0
$13,118B
13100.0
$12,994B
12900.0
% Deviation from Trend (Cycle)
 12, 746  13,118 
*100  2.8%


13,118


$12,746B
12700.0
12500.0
2007
Dec 2007
2009
2011
June 2009
Real GDP
Trend Real GDP
2013