* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 07.01.2015 - Erwin Sitompul
Condensed matter physics wikipedia , lookup
Jerk (physics) wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Work (physics) wikipedia , lookup
First observation of gravitational waves wikipedia , lookup
History of subatomic physics wikipedia , lookup
Classical mechanics wikipedia , lookup
History of fluid mechanics wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Two New Sciences wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Centripetal force wikipedia , lookup
History of physics wikipedia , lookup
Matter wave wikipedia , lookup
Classical central-force problem wikipedia , lookup
Chien-Shiung Wu wikipedia , lookup
Aristotelian physics wikipedia , lookup
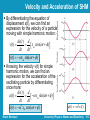
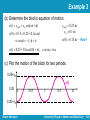
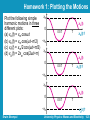
Lecture 1 Ch15. Simple Harmonic Motion University Physics: Waves and Electricity Dr.-Ing. Erwin Sitompul http://zitompul.wordpress.com 2015 Textbook and Syllabus Textbook: “Fundamentals of Physics”, Halliday, Resnick, Walker, John Wiley & Sons, 8th Extended, 2008. Syllabus: (tentative) Chapter 15: Simple Harmonic Motion Chapter 16: Transverse Waves Chapter 17: Longitudinal Waves Chapter 21: Coulomb’s Law Chapter 22: Finding the Electric Field – I Chapter 23: Finding the Electric Field – II Chapter 24: Finding the Electric Potential Chapter 26: Ohm’s Law Chapter 27: Circuit Theory Erwin Sitompul University Physics: Waves and Electricity 1/2 Grade Policy Final Grade = 10% Homework + 20% Quizzes + 30% Midterm Exam + 40% Final Exam + Extra Points Homeworks will be given in fairly regular basis. The average of homework grades contributes 10% of final grade. Homeworks are to be written on A4 papers, otherwise they will not be graded. Homeworks must be submitted on time, at least one day before the schedule of the lecture (at least one day before Monday IE or Tuesday EE). Late submission will be penalized by point deduction of –10·n, where n is the total number of lateness made. But: A homework can be submitted late without penalty if a scanned or photographed version of the homework is sent to [email protected] at least one day before the schedule of the class. Erwin Sitompul University Physics: Waves and Electricity 1/3 Grade Policy There will be 3 quizzes. Only the best 2 will be counted. The average of quiz grades contributes 20% of final grade. Midterm and final exam schedule will follow the schedule given by Academic Administration Bureau. Physics 2 Homework 5 Rudi Bravo 009201700008 21 March 2021 No.1. Answer: . . . . . . . . Heading of Homework Papers (Required) Erwin Sitompul University Physics: Waves and Electricity 1/4 Lecture Activities Extra points will be given if you solve a problem in front of the class or if you send answer to email quizzes. You will earn 1, 2, or 3 points. Make up of quizzes will be held one week after the schedule of the respective quizzes and exams. To maintain the integrity, the score of a make up quiz or exam, upon discretion, can be multiplied by 0.9 (the maximum score for a make up is 90). How to get good grades in this class? • Do the homeworks by yourself • Solve problems in front of the class • Answer email quizzes • Take time to learn at home • Ask questions Erwin Sitompul University Physics: Waves and Electricity 1/5 Lecture Material Lectures will be held in the form of PowerPoint presentations. You are expected to write a note along the lectures to record your own conclusions or materials which are not covered by the lecture slides. Latest lecture slides will be available on internet. Please check the course homepage regularly. The course homepage is : http://zitompul.wordpress.com You are responsible to read and understand the lecture slides. I am responsible to answer your questions. Quizzes, midterm exam, and final exam will be open-book. Be sure to have your own copy of lecture slides. You are not allowed to borrow or lend anything during quizzes or exams. Erwin Sitompul University Physics: Waves and Electricity 1/6 Simple Harmonic Motion The following figure shows a sequence of “snapshots” of a simple oscillating system. A particle is moving repeatedly back and forth about the origin of an x axis. One important property of oscillatory motion is its frequency, or number of oscillations that are completed each second. The symbol for frequency is f, and its SI unit is the hertz (abbreviated Hz). 1 hertz = 1 Hz = 1 oscillation per second = 1 s–1 Erwin Sitompul University Physics: Waves and Electricity 1/7 Simple Harmonic Motion Related to the frequency is the period T of the motion, which is the time for one complete oscillation (or cycle). 1 T f Any motion that repeats itself at regular intervals is called periodic motion or harmonic motion. We are interested here only in motion that repeats itself in a particular way, namely in a sinusoidal way. For such motion, the displacement x of the particle from the origin is given as a function of time by: x(t ) xm cos(t ) Erwin Sitompul University Physics: Waves and Electricity 1/8 Simple Harmonic Motion This motion is called simple harmonic motion (SHM). Means, the periodic motion is a sinusoidal function of time. The quantity xm is called the amplitude of the motion. It is a positive constant. The subscript m stands for maximum, because the amplitude is the magnitude of the maximum displacement of the particle in either direction. The cosine function varies between ±1; so the displacement x(t) varies between ±xm. Erwin Sitompul University Physics: Waves and Electricity 1/9 Simple Harmonic Motion The constant ω is called the angular frequency of the motion. 2 2 f T 2 f radians radians cycles second cycle second The SI unit of angular frequency is the radian per second. To be consistent, the phase constant Φ must be in radians. 2 radians 1 cycle 360 1 radian cycle 180 2 1 cycle 90 4 1 radian cycle 30 6 12 2 Erwin Sitompul radian University Physics: Waves and Electricity 1/10 Simple Harmonic Motion x(t ) xm cos(t ) x(t ) xm' cos(t ) x(t ) xm cos(2t ) x(t ) xm cos(t ) 4 Erwin Sitompul University Physics: Waves and Electricity 1/11 Checkpoint A particle undergoing simple harmonic oscillation of period T is at xm at time t = 0. Is it at –xm, at +xm, at 0, between –xm and 0, or between 0 and +xm when: (a) t = 2T At +xm (b) t = 3.5T At –xm (c) t = 5.25T At 0 (d) t = 2.8T ? Between 0 and +xm 0.5T 1.5T T Erwin Sitompul University Physics: Waves and Electricity 1/12 Velocity and Acceleration of SHM By differentiating the equation of displacement x(t), we can find an expression for the velocity of a particle moving with simple harmonic motion: dx(t ) d v(t ) xm cos(t ) dt dt v(t ) xm sin(t ) Knowing the velocity v(t) for simple harmonic motion, we can find an expression for the acceleration of the oscillating particle by differentiating once more: dv(t ) d a(t ) xm sin(t ) dt dt a(t ) 2 xm cos(t ) Erwin Sitompul a(t ) 2 x(t ) University Physics: Waves and Electricity 1/13 Plotting The Motion Plot the following simple xm harmonic motions: 0 (a) x1(t) = xmcosωt (b) x2(t) = xmcos(ωt+π) –xm (c) x3(t) = (xm/2)cosωt (d) x4(t) = xmcos2ωt x x1(t) 0.5T T x2(t) m x1(t) 0 0.5T T x3(t) –xm xm 0 –xm Erwin Sitompul x1(t) 0.5T T x4(t) University Physics: Waves and Electricity 1/14 The Force Law for Simple Harmonic Motion Now we can use Newton’s second law to learn what force must act on the particle to give it that acceleration: F ma m( 2 x) F (m 2 ) x This result – a restoring force that is proportional to the displacement but opposite in sign – is familiar. It is Hooke’s law for a spring: F kx with the spring constant being k = mω2. Conclusion: Simple harmonic motion is the motion executed by a particle, subject to a force that is proportional to the displacement of the particle but opposite in sign. Erwin Sitompul University Physics: Waves and Electricity 1/15 The Force Law for Simple Harmonic Motion The block–spring system below forms a linear simple harmonic oscillator (or linear oscillator, for short). The relation between the angular frequency ω of the simple harmonic motion of the block is related to the spring constant k and the mass m of the block as follows: k m For the period of the linear oscillator, after combining, we can write: m T 2 k Erwin Sitompul 1 f 2 k m University Physics: Waves and Electricity 1/16 Example 1 A block whose mass m is 680 g is fastened to a spring whose spring constant k is 65 N/m. The block is pulled a distance x = 11 cm from its equilibrium position at x = 0 on a frictionless surface and released from rest at t = 0. (a) What are the angular frequency, the frequency, and the period of the resulting motion? k 65 N m 9.78 rad s, f 1.557 Hz, T 0.642 s 0.68 kg m (b) What is the amplitude of the oscillation? xm 11 cm (c) What is the maximum speed vm of the oscillating block, and where is the block when it has this speed? vm xm (9.78)(0.11) 1.08 m s Erwin Sitompul • Where is the block? University Physics: Waves and Electricity 1/17 Example 1 A block whose mass m is 680 g is fastened to a spring whose spring constant k is 65 N/m. The block is pulled a distance x = 11 cm from its equilibrium position at x = 0 on a frictionless surface and released from rest at t = 0. (d) What is the magnitude am of the maximum acceleration of the block? am 2 xm (9.78)2 (0.11) 10.52 m s2 (e) What is the phase constant Φ for the motion? 0 rad • Why? (f) What is the displacement function x(t) for the spring–block system? x(t ) xm cos(t ) 0.11 m cos(9.78t ), t in seconds Erwin Sitompul University Physics: Waves and Electricity 1/18 Example 2 At t = 0, the displacement x(0) of the block in a linear oscillator is –8.5 cm. The block’s velocity v(0) the is –0.920 m/s, and its acceleration a(0) is +47 m/s2. (a) What is the angular frequency ω of this system? x(0) xm cos v(0) xm sin a(0) 2 xm cos Erwin Sitompul a (0) 47 23.51 rad s x(0) (0.085) University Physics: Waves and Electricity 1/19 Example 2 At t = 0, the displacement x(0) of the block in a linear oscillator is –8.5 cm. The block’s velocity v(0) the is –0.920 m/s, and its acceleration a(0) is +47 m/s2. (b) What are the phase constant Φ and amplitude xm? v(0) sin tan x(0) cos v(0) (0.920) 0.460 tan x(0) (23.51)(0.085) 24.7 ? or 24.7 180 155.3? Since x(0) 0 cos 0 155.3 xm x(0) 0.085 0.0936 m 9.36 cm cos cos155.3 Erwin Sitompul University Physics: Waves and Electricity 1/20 Example 3 A block with m = 500 g is attached to a massless spring and is free to oscillate on a frictionless floor. The equilibrium position is 25 cm from the origin of the x axis. At t = 0, the block is pressed 10 cm from the equilibrium and then released. A force of magnitude 5 N is needed to press the spring. F F kx k x 5N (0.1 m) 50 N m (a) How many oscillations occur in 1 minute? k m (50 N m) (0.5 kg) 10rad s 10 f 2 oscillations s 300 oscillations minute 2 95.493 oscillations minute Erwin Sitompul University Physics: Waves and Electricity 1/21 Example 3 (b) Determine the block’s equation of motion. x(t ) xequil xm cos(t ) xequil 0.25 m xm 0.1 m x(0) 0.15 0.25 0.1cos cos 1, x(0) 0.15 m • How? x(t ) 0.25 0.1cos(10t ), x in m, t in s (c) Plot the motion of the block for two periods. 0.25+xm x(t) 0.25 0 0.5T T 1.5T 2T 0.25–xm Erwin Sitompul University Physics: Waves and Electricity 1/22 Homework 1: Plotting the Motions xm Plot the following simple harmonic motions in three different plots: 0 (a) xa(t) = xmcosωt (b) xb(t) = xmcos(ωt–π/2) –xm (c) xc(t) = xm/2cos(ωt+π/2) xm (d) xd(t) = 2xmcos(2ωt+π) 0 xa(t) 0.5T T xb(t)? xa(t) 0.5T T xc(t)? –xm xm 0 –xm Erwin Sitompul xa(t) 0.5T T xd(t)? University Physics: Waves and Electricity 1/23 Homework 1A: Simple Harmonic Motion 1. Plot the following simple harmonic motions in three different plots: (a) xa(t) = xmsinωt (b) xb(t) = xmsin(ωt–π) (c) xc(t) = xm/2sin(ωt+π/2) (d) xd(t) = xm/2sin(2ωt+π/2) 2. A small car weighs 1200 kg has one spring on each wheel. It can be assumed, that the springs are identical, and that the mass of the car is distributed equally over the springs. (a) Determine the spring constant of each spring if the empty car bounces up and down 2.0 times each second. (b) Determine the car’s oscillation frequency while carrying four 70-kg passengers? Erwin Sitompul University Physics: Waves and Electricity 1/24