Download Newton-Raphson Method Nonlinear Equations

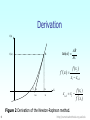
Newton-Raphson Method
Computer Engineering Majors
Authors: Autar Kaw, Jai Paul
http://numericalmethods.eng.usf.edu
Transforming Numerical Methods Education for STEM
Undergraduates
7/29/2017
http://numericalmethods.eng.usf.edu
1
Newton-Raphson Method
http://numericalmethods.eng.usf.edu
Newton-Raphson Method
f(x)
x f x 
f(xi)
i,
i
f(xi )
xi 1 = xi f (xi )
f(xi-1)

xi+2
xi+1
xi
X
Figure 1 Geometrical illustration of the Newton-Raphson method.
3
http://numericalmethods.eng.usf.edu
Derivation
f(x)
f(xi)
tan(  
B
AB
AC
f ( xi )
f ' ( xi ) 
xi  xi 1
C 
A
xi+1
xi
X
f ( xi )
xi 1  xi 
f ( xi )
Figure 2 Derivation of the Newton-Raphson method.
4
http://numericalmethods.eng.usf.edu
Algorithm for NewtonRaphson Method
5
http://numericalmethods.eng.usf.edu
Step 1
Evaluate
6
f (x )
symbolically.
http://numericalmethods.eng.usf.edu
Step 2
Use an initial guess of the root, xi , to estimate the new
value of the root, xi 1 , as
f  xi 
xi 1 = xi f  xi 
7
http://numericalmethods.eng.usf.edu
Step 3
Find the absolute relative approximate error a as
xi 1- xi
a =
 100
xi 1
8
http://numericalmethods.eng.usf.edu
Step 4
Compare the absolute relative approximate error
with the pre-specified relative error tolerance s.
Yes
Go to Step 2 using new
estimate of the root.
No
Stop the algorithm
Is a s ?
Also, check if the number of iterations has exceeded
the maximum number of iterations allowed. If so,
one needs to terminate the algorithm and notify the
user.
9
http://numericalmethods.eng.usf.edu
Example 1
To find the inverse of a number ‘a’, one can use the
1
equation
f ( x)  a 
where x is the inverse of ‘a’.
x
0
Use the Newton-Raphson method of finding roots of
equations to
a) Find the inverse of a = 2.5. Conduct three iterations
to estimate the root of the above equation.
b) Find the absolute relative approximate error at the
end of each iteration, and
c) The number of significant digits at least correct at the
end of each iteration.
10
http://numericalmethods.eng.usf.edu
Example 1 Cont.
Solution
1.5
f ( x)  a 
20
0
f ' ( x) 
0
1
x2
1
0
x
20
f ( x)
xi 1  xi 
40
60
80
 97.5
100
0
0.25
0.01
0.5
x
0.75
1
1
f(x)
Figure 3 Graph of the function f(x).
1
f ( x)  a   0
x
11
f  xi 
f  xi 

1
 a  
xi 
 xi  
 1 
 2 
 xi 

1
 xi  xi2  a  
xi 

 xi  xi2 a  xi
xi 1  2 xi  xi2 a
http://numericalmethods.eng.usf.edu
Example 1 Cont.
Entered function along given interval with current and next root and the
tangent line of the curve at the current root
Initial guess: x0  0.5
Iteration 1
The estimate of the root is
0
2.5
0
18
x1  2 x0  x02 a
 2(0.5)  (0.5) 2 2.5
 0.375
f ( x)
f ( x)
38.5
f ( x)
tan( x)
59
The absolute relative
approximate error is
79.5
 97.5
0
0.24
0.48
0.72
0.96
x x 0  x 1  x
0
f(x)
prev. guess
new guess
tangent line
Figure 4 Graph of the estimated
root after Iteration 1.
12
1.2
1.2
x1  x0
a 
 100
x1
 33.33%
The number of significant
digits at least correct is 0.
http://numericalmethods.eng.usf.edu
Example 1 Cont.
Entered function along given interval with current and next root and the
tangent line of the curve at the current root
4.27778
Iteration 2
The estimate of the root is
0
0
x1  0.375
x2  2 x1  x12 a
2
x2  20.375  0.375 2.5
 0.39844
16.58
f ( x)
37.43
f ( x)
f ( x)
tan( x)
58.29
The absolute relative
approximate error is
79.14
 97.5
0
0.25
0.5
0.75
x x 1  x 2  x
0
f(x)
prev. guess
new guess
tangent
Figure 5 Graph of the estimated
root after Iteration 2.
13
1
1
x2  x1
a 
100
x2
 5.8224%
The number of significant
digits at least correct is 0.
http://numericalmethods.eng.usf.edu
Example 1 Cont.
3.77951
Iteration 3
The estimate of the root is
0
0
x2  0.39844
x3  2 x2  x22 a
2
 20.39844   0.39844  2.5
 0.39999
16.98
f ( x)
f ( x)
37.73
f ( x)
tan( x)
58.49
The absolute relative
approximate error is
79.24
 97.5
0
0.25
0.5
0.75
x x 2  x 3  x
0
f(x)
prev. guess
new guess
tangent
Figure 6 Graph of the estimated
root after Iteration 3.
14
1
1
x3  x2
a 
100
x3
 0.38911%
The number of significant
digits at least correct is 2.
http://numericalmethods.eng.usf.edu
Advantages and Drawbacks
of Newton Raphson Method
http://numericalmethods.eng.usf.edu
15
http://numericalmethods.eng.usf.edu
Advantages


16
Converges fast (quadratic convergence), if
it converges.
Requires only one guess
http://numericalmethods.eng.usf.edu
Drawbacks
1.
Divergence at inflection points
Selection of the initial guess or an iteration value of the root that
is close to the inflection point of the function f x  may start
diverging away from the root in ther Newton-Raphson method.
For example, to find the root of the equation f  x    x  1  0.512  0 .
3
The Newton-Raphson method reduces to xi 1  xi 
x
3
i
 1  0.512
.
2
3xi  1
3
Table 1 shows the iterated values of the root of the equation.
The root starts to diverge at Iteration 6 because the previous estimate
of 0.92589 is close to the inflection point of x  1 .
Eventually after 12 more iterations the root converges to the exact
value of x  0.2.
17
http://numericalmethods.eng.usf.edu
Drawbacks – Inflection Points
Table 1 Divergence near inflection point.
Iteration
Number
18
xi
0
5.0000
1
3.6560
2
2.7465
3
2.1084
4
1.6000
5
0.92589
6
−30.119
7
−19.746
18
0.2000
Figure 8 Divergence at inflection point for
f x   x  1  0.512  0
3
http://numericalmethods.eng.usf.edu
Drawbacks – Division by Zero
2. Division by zero
For the equation
f x   x3  0.03x 2  2.4 106  0
the Newton-Raphson method
reduces to
xi3  0.03xi2  2.4 10 6
xi 1  xi 
3xi2  0.06 xi
For x0  0 or x0  0.02 , the
denominator will equal zero.
19
Figure 9 Pitfall of division by zero
or near a zero number
http://numericalmethods.eng.usf.edu
Drawbacks – Oscillations near local
maximum and minimum
3. Oscillations near local maximum and minimum
Results obtained from the Newton-Raphson method may
oscillate about the local maximum or minimum without
converging on a root but converging on the local maximum or
minimum.
Eventually, it may lead to division by a number close to zero
and may diverge.
2
For example for f x   x  2  0 the equation has no real
roots.
20
http://numericalmethods.eng.usf.edu
Drawbacks – Oscillations near local
maximum and minimum
Table 3 Oscillations near local maxima
and mimima in Newton-Raphson method.
Iteration
Number
0
1
2
3
4
5
6
7
8
9
21
xi
–1.0000
0.5
–1.75
–0.30357
3.1423
1.2529
–0.17166
5.7395
2.6955
0.97678
6
5
f  xi  a %
3.00
2.25
5.063
2.092
11.874
3.570
2.029
34.942
9.266
2.954
f(x)
4
3
3
300.00
128.571
476.47
109.66
150.80
829.88
102.99
112.93
175.96
2
2
11
4
x
0
-2
-1.75
-1
-0.3040
0
0.5
1
2
3
3.142
-1
Figure 10 Oscillations around local
2
minima for f x   x  2 .
http://numericalmethods.eng.usf.edu
Drawbacks – Root Jumping
4. Root Jumping
In some cases where the function f x is oscillating and has a number
of roots, one may choose an initial guess close to a root. However, the
guesses may jump and converge to some other root.

f(x)
For example
1
f x   sin x  0
0.5
Choose
It will converge to
22
x
0
x0  2.4  7.539822
instead of
1.5
-2
0
-0.06307
x0
x  2  6.2831853
2
0.5499
4
6
4.461
8
7.539822
10
-0.5
-1
-1.5
Figure 11 Root jumping from intended
location of root for
f x   sin
. x0
http://numericalmethods.eng.usf.edu
Additional Resources
For all resources on this topic such as digital audiovisual
lectures, primers, textbook chapters, multiple-choice
tests, worksheets in MATLAB, MATHEMATICA, MathCad
and MAPLE, blogs, related physical problems, please
visit
http://numericalmethods.eng.usf.edu/topics/newton_ra
phson.html
THE END
http://numericalmethods.eng.usf.edu