Download *Chapter 1.1 Points Lines Planes Use the figure to name each of the

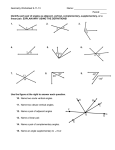
*Chapter 1.1 Points Lines Planes
Use the figure to name each of the
following:
1. five points
A, B, C, D, E
*Chapter 1.2 Measuring Segments
Find the length of the following:
11. Segment AB
3.5
12. Segment BC
2.5
2. two lines
line BD, line AC etc.
3. two planes
Plane J and Plane N
4. point on line BD
C, B, and/or D
13. B is a point between points A and C,
segment AC = 15.8, and segment AB = 9.9.
Find the length of segment BC. (Draw a
picture).
5.9
Draw and label each of the following:
5. a segment with endpoints M and N
check with me
6. three coplanar lines that intersect in a
common point
check with me (3 lines on the SAME
plane that intersect at ONE point)
14. Find the length of segment NP.
7. ray with endpoint F that passes
through G
check with me
NP = 12
8. two lines that do not intersect
check with me (parallel lines)
Use the figure to name each of the
following:
15. K is the midpoint of segment JL, JL =
4x - 2, and JK = 7. Find x, the length of
KL, and JL.
x = 4; KL = 7; JL = 14
9. a line that contains A and C
line AB, line BC, or line AC
10. a plane that contains A, D, and C
Plane M
*Chapter 1.3 Measuring Angles
16. ∠A is an acute angle. ∠O is an obtuse
angle. ∠R is a right angle. Put ∠A, ∠O, and
∠R in order from least to greatest by
measure.
∠A, ∠R, ∠O
22. L is in the interior of ∠JKM. Draw and
label a picture then answer the following:
Check drawing with me
Given: m∠JKL = 42° and m∠LKM = 28°
Find m∠JKM
70°
17. a. Which point is the vertex of ∠BCD?
C
b. Which rays form the sides of ∠BCD?
Ray CB; Ray CD (ORDER MATTERS!)
23. Ray BD bisects ∠ABC. Draw and label
a picture then answer the following:
Check drawing with me
18. Correctly name all 3 angles in the
diagram.
Given: m∠ABD = (6x + 4) ° and m∠DBC =
(8x - 4)°. Find m∠ABD
28°
1. ∠COB
2. ∠AOB
3. ∠COA
*Chapter 1.4 Pairs of Angles
Use the protractor to find the measure of
each angle. Then classify each as acute,
right, or obtuse.
19. ∠VXW
15°; acute
20. ∠TXW
21. ∠RXU
105°; obtuse 110°; obtuse
Tell whether the angles are only adjacent,
adjacent and form a linear pair, or not
adjacent.
24. ∠1 and ∠2
Adjacent and a Linear Pair
25. ∠2 and ∠4
Not Adjacent
26. ∠1 and ∠3
Not Adjacent
27. ∠2 and ∠3
Not Adjacent
*Chapter 2.1 Inductive Reasoning
1. Inductive Reasoning is used to draw a conclusion
from
patterns.
2. A statement you believe to be true based on
Inductive Reasoning is called a
3. Write a valid conditional statement for each of
the following:
a.
conjecture.
If you’re petting a dolphin, then you’re petting a
mammal.
3. To show that a conjecture is true, you must prove
it.
b. You should monitor the heart rate of a patient who
is ill.
4. To show that a conjecture is false, you can give a
counterexample.
If a patient is ill, you should monitor their heart rate.
5. Complete each conjecture:
a. A pair of complementary angles have a sum of
90°
4. A Conditional Statement has a truth value of
either True or False.
5. Write each statement in terms of p and q:
a. Conditional: p
b. The square of any negative number is always
positive.
6. Show that each conjecture is false by providing
a counterexample:
q
b. Converse: q
p
c. Inverse: ~p
~q
d. Contrapositive: ~q
a. Two angles that have the same vertex are adjacent.
EX: A pair of vertical angles have the same
vertex but are NOT adjacent!
b. If x + 1 > 5, then x = 8
~p
6. Write the converse, inverse, and contrapostive
of the following conditional statement and
determine the truth value for each condition.
If a figure has 4 sides, then it is a rectangle.
EX: x = 6 (answers may vary)
a. T or F Converse:
*Chapter 2.2 Conditional Statements
If it’s a rectangle, then it has 4 sides. TRUE
1. A Conditional Statement is a statement that can be
written in the form:
If p, then q.
b. T or F Inverse:
If it does NOT have 4 sides, then it is NOT a
rectangle. TRUE
2. Underline the hypothesis and circle the
conclusion of each conditional statement.
a. If the weather is nice, then I will go outside.
b. Angles are complementary if they add up to 90.
c. T or F Contrapositive:
If it’s NOT a rectangle, then it does NOT
have 4 sides. FALSE
*Chapter 2.3 Deductive Reasoning
1. Deductive Reasoning is used to draw a
conclusions from given fact, definition, and
postulates/theorems.
4. Write the following definition as a valid
Biconditional Statement:
A right angle has a measure of 90 degrees.
An angle is right if and only if it measure 90°.
If two angles are supplementary, then they have a
sum of 180.
Given:  A and  B are supplementary.
5. Using the Biconditional you wrote in #4,
determine if it’s a true Biconditional Satement
and explain how you know.
Conditional: If an angle is right, then it measures 90°.
Converse: If an angle measures 90°, then it’s a right
angle.
Because BOTH the conditional and its converse are
true, the biconditional is true.
Therefore:
*Chapter 2.5 Algebraic Proofs
2. Use the Law of Detachment in order to give a
valid conclusion:
∠A and ∠B have a sum of 180°
3. Use the Law of Syllogism and give a valid
conclusion:
If two lines intersect, then they are not parallel. If two
lines are not parallel, then they have different slopes.
Given: Line m and line r intersect at point, P.
Therefore:
Line m and line r have different slopes.
*Chapter 2.4 Biconditional Statements and
Definitions
1. A Biconditional Statement is written in
the form: p IF AND ONLY IF (IFF) q
which means p
q and q
p
2. A defintion is a statement that can be
written as a TRUE Biconditional.
3. In order for a Biconditional Statement to
be TRUE, both the conditional statement
AND its converse must be true.
State which property, postulate,
definition, or theorem supports each
statement below.
1. If R is in the interior of PQS,
then mPQR + mRQS = mPQS.
Angle Addition Postulate (helps to draw a picture)
2. If 1 and 2 are supplementary,
then m1 + m2 = 180.
Definition of supplementary angles
3. If 1  2 and 2  3, then 1  3.
Transitive Property of Congruence
4. If M is the midpoint of AB ,
then AM  MB .
Definition of midpoint
5. If AB = CD, then AB + EF = CD + EF.
Addition Property of Equality (added EF to both
sides of the original equation)
6. 1 and 2 form a linear pair,
then they are supplementary.
Linear Pair Theorem
7. If mA + mB = 90,
then A and B are complementary.
Definition of complementary angles
8. If BX bisects ABC ,
then m  ABX = m  XBC.
Definition of angle bisector
9. AB  AB
Reflexive Property of Congruence
10. If AM = MB, then AM  MB .
Definition of congruence
11. If 1 and 2 are supplementary AND
2 and 3 are supplementary, then 1  3.
Congruent Supplements Theorem
12. If X and Y are right angles,
then X  Y.
Right Angle Congruence Theorem
13. Complete the following Algebraic Proof by
listing each step and providing its justification.
1. -2(x +5) = -6
1. Given
2. -2x – 10 = -6
2. Distribution
3. -2x = 4
3. Addition Prop. of Equality
4. x = -2
4. Division Prop. of Equality
*Chapter 2.6 Geometric Proofs
PRACTICE ALL PROOFS!!