Download LECTURE 6

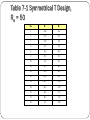
Attenuators
 Attenuators are simple but very important instruments.
Unlike an amplifier, which is ordinarily used to increase
a signal level by a given amount, the attenuator is used to
reduce the signal level by a given amount.
 The use of attenuators has become so widespread that a
study of their design and use is important in the study of
electronic instruments. Attenuators may be constructed
in many ways. We will confine our discussion to lumpedresistance attenuators.
The L-type Attenuator
 One of the simplest types of attenuators is the L type or
the ordinary voltage divider. The voltage gain of this
network is the output voltage divided by the input
voltage.
 We can find the formula for gain in the following
manner:
 out  iR 2
 out
 in
R2

R2 
 in
R1  R2
R1  R2
out
R2
A

in R1  R2
(1)
 Equation (1) should be familiar. It tells us that the voltage
gain of a simple voltage divider is equal to R2 divided by
the sum of R1 and R2.
 For instance, if R1 equals 9 kilo-ohms and R2 equals 1
kilo-ohm the voltage gain equals one-tent. As usual, to
find the voltage gain expressed in decibels, we take 20
times the base 10 logarithm of A. In this case, for A
equals 0.1, Adb equals -20 db.
 Since attenuators always reduce the signal level, the value
of A is always less than unity, and Adb is therefore always
negative. If we like, we can use the reciprocal of A and
thereby avoid values that are less than unity. In other
words, let us define the attenuation as:
 in 1
a

 out A
(2)
 For the voltage divider with R1 equal to 9 kilo-ohms and
R2 equal to 1 kilo-ohm, we now say that the attenuation
a is 10, or adb is 20 db. The distinction between A and a is
merely a detail, but it should be understood, since both
terms are commonly used in practice.
The Characteristic Resistance of Symmetrical
Attenuators
 Usually, the term attenuator refers to a device that not
only introduces a precise amount of attenuation but also
provides an impedance match on the input and output
terminals.
 For instance, an attenuator has been inserted between a
source and a load. If it has been properly designed, the
input resistance will be 50ohms, thereby matching the
source resistance.
 Further, at the output terminals, the Thevenin resistance
looking back is 50ohms, so that the load is matched.
 There are many systems where impedance matching is
very important.
 In fact, in any system using transmission lines a great deal
of trouble maybe encountered unless all devices are
impedance-matched.
fig.2
fig.3
This is especially true in those situations where the
wavelength associated with the signal becomes
comparable to the length of the transmission line.
Telephone, television, and microwave systems are
example situations where impedance matching is
normally used.
 We will now be concerned with attenuators that have
been designed to provide an impedance match on both
the input and output side. Further, we will confine our
attention to a practical class attenuators known as
unbalanced symmetrical attenuators.
 The two most basic forms in this class are shown in Fig.
7-3 (a) and (b). Note that these are symmetrical about
vertical center line. The word "unbalanced" refers to the
fact that there is a common connection from input to
output (the lower wire).
 One extremely important property of symmetrical
attenuators is what is commonly referred to as the
characteristic (or image) resistance
 Consider the situation in Fig. 7-4. A variable-load resistor
has been connected to the output of the attenuator.
fig.4
 As we look into the attenuator, we see a value of input
resistance that depends upon the value of load resistance.
Suppose that for RL = 100 ohms, Rin = 60 ohms. As we
change RL to 70 ohms, we might observe that Rin
changes to 55 ohms.
 As we vary RL again to a new value of 50 ohms, we
might have an Rin equal to 50 ohms. Continuing in this
way, we would find that Rin takes on different values for
each value of RL
 In general, the characteristic resistance of an attenuator
is that value of load on an attenuator which produces the
same value of input resistance. Every attenuator has a
characteristic resistance. Under normal circumstances,
attenuators should always be loaded in their
characteristic resistances. If this is done, the resistance
value is maintained throughout the system in which the
attenuator is used.
 For instance, if a system uses 50-ohm load resistors and
50-ohm source resistances, using an attenuator with a
characteristic resistance of 50 ohms between a load and a
source will match the impedance on the source and load
sides of the attenuator.
 A useful formula for the characteristic resistance Ro of an attenuator is
Ro  Rins Rino
(3)
 where Rins : is the input resistance of the attenuator with the output
terminals shorted .

Rino : is the input resistance of the attenuator with the output
terminals open. This equation can be derived by use of z para meters.
We will accept it without derivation.
Symmetrical T Analysis Formulas
 In this section we wish to find a pair of formulas that will be
useful whenever we have to deal with the symmetrical T
attenuator. In order to simplify the formulas it is helpful to
define the ratio of R2 to RI as follows:
R2
m
R1
or
R2 = mR1
(4)
(5)
 With this definition for m, the attenuator may be relabeled
fig. 5
 First, let us find Ro
Ro  Rins Rion  ( R1  R1 mR1 )( R1  mR1 )
After a few simplifying algebra steps we can
obtain :
Ro = R1 1 2m
(6)
(7)
 The second formula that will be useful in our work is a
formula for the amount of attenuation that takes place
from the input to the output terminals of an attenuator
loaded in its characteristic resistance .
 We require a formula for , that is, the attenuation. There
are several approaches that can be used in finding such an
expression. We will merely note that after the required
algebra, it can be shown that
(8)

1  m  1  2m
a
in
 out

m
fig. 6
 Let us summarize. In Eqs. (7-7) and (7-8) we have the
analysis formulas for a symmetrical T attenuator. Given the
values of R1 and R2 (such as on a schematic), we can find m
by taking the ratio of R2 to R1. Then, substituting into Eqs.
(7-7) and (7-8) we can easily find the characteristic resistance
and the attenuation for the T attenuator.
EXAMPLE 5:
 Compute the characteristic resistance and the attenuation of
a symmetrical T attenuator which has R1 = 409Ω
and R2 = 101Ω .
SOLUTION:
m
R2 101

 0.247
R1 409
Ro  R1 1  2m  409 1  2(0.247)  500 ohms
a
1  0.247  1  2(0.247)
0.247
 10
 Thus, the given attenuator should be used with a 500-ohm
load and source resistance. If this is done, the attenuation will
be equal to 10, which is equivalent to 20 db.
EXAMPLE 6:
 If the attenuator of Example 5 has all resistances reduced by a
factor of ten, what is the value of Ro and a for the new
attenuator?
SOLUTION:
 We note that now R1 = 40.9 and R2 = 10.1 ohms. Therefore,
m still equals 0.247, as in Example 5. From Eq. (8), the
attenuation still equals 10.
 Next, we observe from Eq. (7) that R, is directly
proportional to R1. The value of m is still the same.
Therefore, Ro equals one-tenth of 500, or 50 ohms.
 Thus, by reducing all resistances by a factor of ten, we have
reduced the characteristic resistance by ten, but the
attenuation has remained the same.
5- Symmetrical T Design Formulas:
 In this section we develop design formulas for the
symmetrical T attenuator. Equations (7) and (8) tell us how
to find Ro and a, given the value of R1 and R2. If, on the other
hand, we wish to design a T attenuator, ice will be given the
value of Ro and a and will need to find R1 and R2. We can find
formulas for R1 and R2 by solving Eqs. (7) and (8)
simultaneously.
5- Symmetrical T Design Formulas:
 If this is done, we obtain:
a 1
R1 
Ro
a 1
R2 
2a
Ro
2
a 1
(9)
(10)
These are very useful formulas for designing T attenuators. For
instance, if the characteristic resistance is to be 50 ohms, and if the
attenuation is to be 10,
5- Symmetrical T Design Formulas:
 we would obtain
R1 
R2 
10  1
50  40.9 ohms
10  1
2(10)
50  10.1 ohms
10 2  1
From Eqs. (9) and (10) it should be clear that R1 and R2 are
functions of a and Ro. Note especially that R1 and R2 are
directly proportional to Ro. If we like, we can generate a
table of design values for future reference. In order to
simplify the table we may choose Ro equal to 50 ohms.
5- Symmetrical T Design Formulas:
 With Ro equal to 50 ohms, R1 and R2 become functions of a
only. To make a table we can select values of a and calculate
the corresponding values of R1 and R2, as shown in Table 1.
 Note that for any characteristic resistance not equal to 50
ohms, we need only multiply each value for R1 and R2 by
Ro/50. For instance, if we need a 500-ohm 20-db attenuator,
according to our table, the value of R1 and R2 should be 40.9
and 10.1 ohms, respectively, for a 50-ohm attenuator.
5- Symmetrical T Design Formulas:
 For a 500-ohm attenuator we need only multiply each R1 and
R2 value by , or 10. Thus, we obtain R1 = 409 and R2 = 101
ohms for a 20-db 500-ohm attenuator.
EXAMPLE 7 :
 Design a 12-db 50-ohm T attenuator.
SOLUTION:
From Table 1 we find R1 = 29.9 and R2 = 26.8 ohms. Since
the attenuator resistance is to be 50 ohms, these values are
used as they are.
Table 7-1 Symmetrical T Design,
Ro = 50
Ddb
R1
R2
1
2.88
433
2
5.73
215
3
8.55
142
4
11.3
105
6
16.6
66.9
8
21.5
47.3
10
26
35.1
12
29.9
26.8
16
36.3
16.3
20
40.9
10.1
24
44.1
6.34
28
46.3
3.99
30
46.9
3.17
35
48.3
1.78
40
49
1.00
EXAMPLE 8:
 Design a 20-db 600-ohm T attenuator.
SOLUTION:
From Table 1 we find R1 = 40.9 and R2 = 10.1 ohms. Since
the characteristic resistance is to be 600 ohms, we must
multiply R1 and R2 by , or 12. If we do this, we obtain R1 =
490 and R2 = 121 ohms.
6- Cascading T Sections:
 Up to this time we have dealt only in basic T attenuators, that
is, a single T composed of three resistors. Basic T sections
may be cascaded, as shown in Fig. 9.
Fig. 9 Cascading symmetrical T sections.
6- Cascading T Sections:
 Note that the resistance level is preserved as we move from
load to source. That is, starting from the load end, we see
that the input resistance of the second attenuator is Ro. This
means that the first attenuator is also loaded correctly in its
characteristic resistance. As a result, the input resistance of
the first attenuator is also equal to Ro. This useful property of
attenuators allows us to cascade as many attenuators as we
like. The Ro resistance is preserved throughout the entire system, with the result that a perfect impedance match occurs at
all input and output terminals.
6- Cascading T Sections:
 There is a good reason for wanting to cascade attenuator
sections. From Table 1 note that as we approach higher values
of attenuation, R2 becomes very small. Because of this, values
of attenuation above 40 db will require R2 values that are
impracticably small. Therefore, in the construction of, say, a
90-db attenuator, we can cascade three 30-db sections.
6- Cascading T Sections:
 For instance, if we wish a 90-db 50-ohm attenuator, we
obtain R1 = 46.9 ohms and R2 = 3.17 ohms for each 30-db
section. After cascading the 30-db sections, we have the
circuit shown in Fig. 10a. The 46.9-ohm resistances can be
lumped into a single 93.3-ohm resistor,
 Fig. 10 (a) Three-section T attenuator. (b) Combining resistances.
6- Cascading T Sections:
 as shown in Fig. 10b. This circuit has characteristic resistance
of 50 ohms and an attenuation of 90 db.
 EXAMPLE 9:
 Design a 50-db 500-ohm attenuator using three basic T
section.
6- Cascading T Sections:
 SOLUTION
Arbitrarily, we can choose to use two 20-db sections and one
10-db section. For the 20-db section we obtain from Table 1
R1 = 40.9
and R2 = 10.1 ohms for Ro = 50 ohms
or
R1 = 409 and R2 = 101 ohm for Ro = 500 ohms
 For the 10-db section we obtain
 R1 = 26
and
R2 = 35.1 ohms
ohms
 or
 R1 = 260
and R2 = 351 ohms
ohms
The final design is shown in Fig. 11
Fig. 11 Example 9.
for Ro = 50
for Ro = 500
7- The Symmetrical  Attenuator
 The
section of Fig. 12a is as basic as the T section.
Occasionally, the  section may be preferred to the T
section. By defining m as the ratio
Fig. 12
 of R2 to R1, we can reliable the values as shown in Fig. 12b.
Proceeding as we did for the T section, we can find the
following formulas for analysis and design:
Analysis
Ro 
m
1  2m
R1
1  m  1  2m
a
m
(11)
(12)
 Design
a 2 1
R1 
Ro
2a
(13)
a 1
Ro
a 1
(13)
R2 
As with the T section, we can generate a table for future reference.
Table 2 gives the design values of R1 and R2 for a characteristic
resistance of 50 ohms. For any other value of Ro, we need only
multiply R1 and R2 by Ro/50.
Design, Ro = 50
Table 2 Symmetrical

Ddb
R1
R2
1
5.77
870
2
11.6
436
3
17.6
292
4
23.8
221
6
37.4
150
8
52.8
116
10
71.2
96.2
12
93.2
83.5
16
154
68.8
20
248
61.1
24
395
56.7
30
790
53.3
40
2500
51
EXAMBLE 10:
 Design a 20-db 300-ohm  attenuator.
 SOLUTION :
 From Table 2 we see that R1 = 2-18 and R2 = 61.1 ohms for
an Ro of 50 ohms. For an Ro of 300 ohms we must multiply
by 300/50, or 6. Hence, R1 = 1488 and R2 = 366.6 ohms.
7-The Bridged T Attenuator
 The last specific type of attenuator we wish to study is the
bridged T attenuator. The circuit for a bridged T is shown in
Fig. 13.The reason
Fig. 13 Bridged T Attenuator
 for the name bridged T should be clear. To an ordinary T
attenuator is added a resistor that bridges from the input to
the output. The analysis and design formulas for this
important attenuator are as follows:
Analysis
Ro  R1
(15)
R1
a
1
R2
(16)
 Design
R1  Ro
R2 
Ro
a 1
R3  (a  1) Ro
(17)
(18)
Note carefully that tote design formulas indicate that R1 is not
a function of a. Only R2 and R3 depend upon a. This is a very
important property, as will be discussed in the next section.
EXAMPLE 11
 Design a 20-db 50-ohm bridged T attenuator.
SOLUTION
 R1 = 50 ohm
R2 
50
 5.55 ohms
10  1
R3  (10  1) 50  450 ohms
9 -Variable Attenuators
 Commercial instrument attenuators are often of the variable
type to allow selection of different values of attenuation,
while maintaining the resistance at the value of Ro. One way
of building a continuously variable attenuator is by using
ganged rheostats for the resistors in the attenuator.
 In either the T or the attenuator all three resistances must
be varied in accordance with the design equations. It is
actually much easier to use a bridged T attenuator. Recall that
the R1 value does not depend upon the amount of
attenuation. R1 may be fixed at the value of characteristic
resistance that is desired.
9 -Variable Attenuators
 We need only vary R2 and R3, as shown in Fig. 14. Note that
R2 and R3 are ganged together. In order to work properly,
Fig. 14 Continuously variable attenuator
9 -Variable Attenuators
 these rheostats must track according to Eqs. (17) and (18). In
these equations we note that R2 is inversely proportional to a,
whereas R3 is directly proportional to a. A study of these
equations shows that linear rheostats will not track properly.
However, logarithmic rheostats can be ganged together, so
that Eqs. (17) and (18) are satisfied. The result is then a
continuously variable attenuator whose characteristic
resistance remains constant.
9 -Variable Attenuators
 Of course, the tracking of R2 and R3 cannot be made perfect.
Some deviation in the value of Ro is to be expected.
However, the variable bridged T attenuator provides a
reasonably accurate value of Ro over its range of adjustment.
 If more precise values of Ro and a are required, the usual
procedure is to build a step attenuator, which is an attenuator
varied in discrete steps. For instance, a step attenuator might
be designed to cover from 0 to 10 db in steps of 1 db. We
would then be able to select 0, 1, 2, 3, or any whole number
of decibels up to 10 db.
9 -Variable Attenuators
 One of the most popular ways of building a step attenuator is
by building a number of simple T attenuators with different
values of attenuation. By means of a proper switching
arrangement, various combinations can be cascaded to
produce the desired amount of attenuation. For example,
suppose we desire to build a 0- to 10-db attenuator with 1-db
steps. We could build four basic attenuators with values of 1,
2, 3, and 4 db.
9 -Variable Attenuators
 There are several switching arrangements that can be used to
switch in any attenuation from 1 to 10 db, simply by using
combinations of the four basic attenuators. To obtain 6 db, for
example, the 2- and 4-db attenuators must be cascaded. To
obtain 9 db, we must connect the 2-, 3-, and 4-db attenuators
(see Prob. 16).
9 -Variable Attenuators
 A 100-db attenuator with 1-db steps can be made by using
two step attenuators in cascade. The first unit would be a 0to 10-db step attenuator with 1-db steps. In cascade with
this, we would use a 0- to 90-db attenuator with 10-db steps.
Thus, any whole number of decibels between 0 and 100 db
can be selected.