* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 6-2 Matrix Multiplication Inverses and Determinants page 383 17 35
Matrix completion wikipedia , lookup
Capelli's identity wikipedia , lookup
Linear least squares (mathematics) wikipedia , lookup
Rotation matrix wikipedia , lookup
Eigenvalues and eigenvectors wikipedia , lookup
Four-vector wikipedia , lookup
Principal component analysis wikipedia , lookup
Jordan normal form wikipedia , lookup
Singular-value decomposition wikipedia , lookup
Matrix (mathematics) wikipedia , lookup
Perron–Frobenius theorem wikipedia , lookup
Non-negative matrix factorization wikipedia , lookup
System of linear equations wikipedia , lookup
Orthogonal matrix wikipedia , lookup
Matrix calculus wikipedia , lookup
Determinant wikipedia , lookup
Cayley–Hamilton theorem wikipedia , lookup
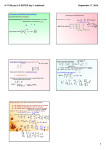
6-2 Matrix Multiplication, Inverses and Determinants Write each system of equations as a matrix equation, AX = B. Then use Gauss-Jordan elimination on the augmented matrix to solve they system. 17. SOLUTION: Write the system matrix in form AX = B. Make sure you align the variables. For the first matrix, the first column should include x1, the second column x2, and the third column x3. The column matrix and the matrix of constant terms should be listed in order. · = Write the augmented matrix . Attach the matrix of constant terms to the end of the 3 × 3 matrix. Use Gauss-Jordan elimination to solve the system. First, use elementary row operations to transform A into I. eSolutions Manual - Powered by Cognero Page 1 Write the augmented matrix . Attach the matrix of constant terms to the end of the 3 × 3 matrix. 6-2 Matrix Multiplication, Inverses and Determinants Use Gauss-Jordan elimination to solve the system. First, use elementary row operations to transform A into I. The solution of the equation is given by X. Therefore, the solution is (14, 5, 6). Find the determinant of each matrix. Then find the inverse of the matrix, if it exists. 35. eSolutions Manual - Powered by Cognero SOLUTION: Find the determinant. Page 2 Find the determinant of each matrix. Then find the inverse of the matrix, if it exists. 6-2 35. Matrix Multiplication, Inverses and Determinants SOLUTION: Find the determinant. = ad − bc det(A) = |A| = Because the determinant is not 0, the matrix is invertible. Find the inverse matrix. Confirm that AA 37. −1 −1 = A A = I. eSolutions Manual - Powered by Cognero SOLUTION: Page 3 6-2 Matrix Multiplication, Inverses and Determinants 37. SOLUTION: Find the determinant. = ad − bc det(A) = |A| = Because the determinant is not 0, the matrix is invertible. Find the inverse matrix. Confirm that AA −1 −1 = A A = I. eSolutions Manual - Powered by Cognero Page 4 6-2 Matrix Multiplication, Inverses and Determinants 39. SOLUTION: Find the determinant. det(A) = |A| = = Because the determinant is not 0, the matrix is invertible. Use a graphing calculator to find the inverse matrix. Use the Frac feature under the MATH menu to write the inverse using fractions. eSolutions Manual - Powered by Cognero Therefore, A –1 = Page 5 . 6-2 Matrix Multiplication, Inverses and Determinants 39. SOLUTION: Find the determinant. det(A) = |A| = = Because the determinant is not 0, the matrix is invertible. Use a graphing calculator to find the inverse matrix. Use the Frac feature under the MATH menu to write the inverse using fractions. Therefore, A –1 = . 41. SOLUTION: Find the determinant. det(A) = |A| = = eSolutions Manual - Powered by Cognero Page 6 Therefore, A –1 = . 6-2 Matrix Multiplication, Inverses and Determinants 41. SOLUTION: Find the determinant. det(A) = |A| = = Because the determinant is 0, the matrix is singular and the inverse does not exist. 43. SOLUTION: Find the determinant. det(A) = |A| = = Because the determinant is not 0, the matrix is invertible. Use a graphing calculator to find the inverse matrix. eSolutions Manual - Powered by Cognero Page 7 determinant is 0, theInverses matrix is singular and the inverse does not exist. 6-2 Because MatrixtheMultiplication, and Determinants 43. SOLUTION: Find the determinant. det(A) = |A| = = Because the determinant is not 0, the matrix is invertible. Use a graphing calculator to find the inverse matrix. Use the Frac feature under the MATH menu to write the inverse using fractions. Therefore, A –1 = . Find the area A of each triangle with vertices (x 1, y 1), (x 2, y 2), and (x 3, y 3), by using A = X is . eSolutions Manual - Powered by Cognero 45. , where Page 8 Therefore, A –1 = . 6-2 Matrix Multiplication, Inverses and Determinants Find the area A of each triangle with vertices (x 1, y 1), (x 2, y 2), and (x 3, y 3), by using A = X is , where . 45. SOLUTION: 47. SOLUTION: eSolutions Manual - Powered by Cognero Page 9 6-2 Matrix Multiplication, Inverses and Determinants 47. SOLUTION: Given A and AB , find B. 49. A = , AB = SOLUTION: Let B = . Set up two systems of equations. Solve for w, y, x, and z. eSolutions Manual - Powered by Cognero Page 10 6-2 Matrix Multiplication, Inverses and Determinants Given A and AB , find B. 49. A = , AB = SOLUTION: Let B = . Set up two systems of equations. Solve for w, y, x, and z. Solve the next system. B= = eSolutions - Powered by Cognero FindManual x and y. 51. A = ,B= , and AB = Page 11 = = 6-2 BMatrix Multiplication, Inverses and Determinants Find x and y. 51. A = ,B= , and AB = SOLUTION: eSolutions Manual - Powered by Cognero Page 12