Download Investigate Points of Concurrency Using GSP GSP File

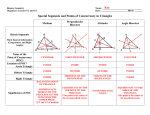
Investigate Points of Concurrency Using GSP
GSP File due Wednesday, January 30 at 2:30 pm (20 points)
In this activity, you will construct the incenter, circumcenter, centroid, and orthocenter of a
triangle using Geometer’s Sketchpad (GSP).
Each sketch should be on a separate page of your file. To create a new page, from the FILE
menu, select DOCUMENT options and ADD PAGE – Duplicate the previous page.
Label each sketch using a text box with a description. Name the point or line segment
created in the sketch in your description. Also, use a text box to write the definition of
each point of concurrency.
When completed, save ONE file with each sketch on a different page on the STUDENTS drive
in your period’s folder in the INVESTIGATING POINTS OF CONCURRENCY folder. Name
your sketch with your full name, last name first (for example George Washington would name
his file washingtongeorge).
Let’s begin! Open a new sketch and draw triangle ABC by constructing three points and then
constructing the segments between them.
1. Using triangle ABC, construct the angle bisectors and the incenter using the following
steps. Recall the incenter is the intersection of the angle bisectors and is the center of the
inscribed circle.
 To construct the angle bisectors: select each angle by selecting the angle’s vertices,
choosing the vertex second. Using the CONSTRUCT menu, construct the angle
bisector for each angle.

To construct the incenter: select any two of these lines and construct the point of
intersection D.

To keep things "tidy," select the angle bisectors (rays) using the select button (arrow)
and then using the HIDE command from the DISPLAY menu.

To construct the inscribed circle: select segment AB and point D.
o Using the CONSTRUCT menu, construct a PERPENDICULAR LINE.
o Select this line and segment AB and construct the point of intersection, E.
o Construct segment DE.
o Select the segment DE and point D and construct the circle using the
CONSTRUCT menu Circle By Center+Radius command.

On your sketch, you have constructed the incenter D and the inscribed circle. Hide
segment DE and point E.

Save this sketch on page one of your file. Don’t forget to label your sketch, naming the
point and giving the definition of the incenter in a text box.
2. Add a new page by going to the FILE menu and choosing DOCUMENT options and ADD
PAGE – Duplicate the previous page. Using triangle ABC, construct the circumcenter using
the following steps. Recall that the circumcenter is the intersection of the perpendicular
bisectors of the sides of the triangle.
 To construct the midpoints: select segment AB and, using the CONSTRUCT menu,
construct the midpoint and label it F.

To construct a perpendicular bisector, select F and segment AB and in the Construct
menu select Perpendicular Line.

Repeat this construction for the remaining sides of the triangle (label the other midpoints
G and H).

To construct the circumcenter: select any two of these lines and construct the point of
intersection M.

To keep things "tidy," hide the perpendicular lines.

To construct the circumscribed circle: select the center M and a point on the circle.
o Select one of the points A, B, or C then select center M.
o Select the Circle By Center+Point command from the Construct menu.

On your sketch, you have constructed the circumcenter M and the circumscribed circle.
Hide the circumscribed circle and the line. Do not hide F, G, and H since you will be
using them to construct the centroid later.

Save this sketch on page two of your file. Don’t forget to label your sketch, naming the
point and giving the definition of the circumcenter in a text box.
3. Add a new page by duplicating the previous one. Using triangle ABC, construct the centroid
using the following steps. Recall that the centroid is the intersection of the medians of the
triangle. A median extends from a vertex to the midpoint of the opposite side.
 To construct the medians of the triangle: use midpoints F, G, and H from the previous
construction.

Use the vertices of the triangle and the midpoints of the opposite sides to construct the
medians. Construct segments AG, BH, and CF. Your segments could be named
differently.

To construct the centroid, select any two medians and construct the point of intersection
J.

Hide the medians and points F, G, and H.

Save this sketch on page three of your file. Don’t forget to label your sketch, naming the
point and giving the definition of the centroid in a text box.
4. Add a new page by duplicating the previous one. Using triangle ABC, construct the
orthocenter using the following steps. Recall that the orthocenter is the intersection of the
altitudes of the triangle. An altitude is the perpendicular line from a vertex to the opposite
side.
 To construct an altitude, select point A and its opposite side BC. From the
CONSTRUCT menu, select PERPENDICULAR LINE.
5.

Repeat the construction for vertex B and opposite side AC and vertex C and opposite
side AB.

To construct the orthocenter: select any two altitudes and construct the point of
intersection K.

On your sketch, you have constructed the orthocenter K. Hide the perpendicular lines.

Save this sketch on page four of your file. Don’t forget to label your sketch, naming the
point and giving the definition of the orthocenter in a text box.
Add a new page by duplicating the previous one. Notice that the circumcenter, centroid,
and orthocenter (points M, J and K) always lie on a line.
 Drag the vertices of the triangle to investigate.

If the triangle is isosceles, where are all the points of concurrency?

If the triangle is equilateral, where are all the points of concurrency?

You may be able to see these relationships more clearly if you first construct the
segment defined by the orthocenter and circumcenter, KM. Construct KM and recheck
the points. This segment is part of the Euler Line.

This sketch should be page five of your file. Label this sketch “The Euler Line.”
The Euler line is most famous line studied in the subject of triangle geometry. It was named in
honor of Leonhard Euler (pronounced OY-Ler), a famous mathematician who lived from 17071783. Euler was a prolific mathematician who introduced much of the mathematical notation
we use today such as f ( x)and  , modern notation for the trigonometric functions, e (Euler’s
number) to represent the base of the natural logarithm, and the letter i to denote the
imaginary unit. He also popularized the use of  to represent the ratio of a circle’s
circumference to its diameter. Euler discovered the properties of the Euler Line when trying to
prove the existence of a triangle by using the four “centers.” One of the things that makes the
Euler Line so interesting is that if you vary the shape of triangle ABC, the relative distances
between certain points on the line remain the same. For example, the distance from the
centroid to the circumcenter is half the distance from the centroid to the orthocenter. Many
other well-known points that we are not studying this year lie on the Euler Line; most of them
were first studied by mathematicians after 1980.