* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Astronomy 114 Problem Set # 5 Due: 04 Apr 2007 SOLUTIONS 1 1
Survey
Document related concepts
Transcript
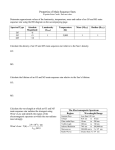
Astronomy 114 Due: Problem Set # 5 04 Apr 2007 SOLUTIONS 1 1 ton of TNT produces an explosion with an energy of 4.2 × 109 joules (1 ton = 907 kg). How much mass is converted into energy in such an explosion? According to Einstein mass-energy equation: E = mc2 . The amount of mass that must be converted to energy to produce as much energy as the TNT explosion is found by solving the above equation for mass: m= E 4.2 × 109 = kg = 4.67 × 10−8 kg c2 (3 × 108 )2 2 If the entire mass of the TNT in the last problem were completely converted into energy, how much energy would be released? According to Einstein mass-energy equation, the released energy is: E = mc2 = 907 × (3 × 108 )2 joules = 8.16 × 1019 joules. Note that this is ten orders of magnitude larger than the chemical TNT explosion. This should help give you some feel for the power in fusion reactions. 3 The Sun has a luminosity of 3.83 × 1026 joules/sec. How much mass does the Sun lose each second? According to solar luminosity, each second the energy that the sun gives out is 3.83 × 1026 joules, then from Einstein mass-energy equation, each second the mass the Sun lose is: m= E 3.83 × 1026 = kg = 4.26 × 109 kg 2 8 2 c (3 × 10 ) Note that at the Sun’s main-sequence age (1010 years), the Sun will have lost: 4.26 × 109 kg/s × 1010 years364.25 hours s days × 24 × 3600 = 1.3 × 1027 kg year day day which is 0.1% of the Suns’ total mass. 4 The central star in a newly formed planetary nebula has a luminosity of 1000 L⊙ and a surface temperature of 100,000 K. How big is the star? The luminosity for a star is L=4πR2 σT 4 , thus we can get R2 T 4 L = = L⊙ R⊙ 2 T⊙ 4 so R = R⊙ thus v u u LT⊙ 4 t L⊙ T 4 = s R R⊙ !2 T T⊙ !4 1000 × 58004 = 0.11 1000004 R = 0.11R⊙ = 7.66 × 107 m 5 The energy-generation rate in a star depends sensitively on the core temperature. Use this fact to explain why a relation between a star’s mass and its luminosity should exist, and why it is not surprising that L ∝ M 3.5 rather than just L ∝ M. One’s first guess might be that the L ∝ M since a larger star will have proportionately more mass available for fusion reactions. However, the larger stellar mass exerts a larger pressure on the star’s core and increases its temperature. Since the luminosity depends on the the energy-generation rate and the energy generation rate increases rapidly with temperature, the total luminosity will increase more steeply than a simple linear proprotionality. For example, if the core temperature were proportional to mass and the energy generation rate were proportional to T 2 , we would estimate that L ∝ M 3 , one power of M for the larger overall mass available for fusion and M 2 for the increased fusion rate due to temperature. A detailed calculation taking the mass, pressure, and details of the nuclear energy generation rate into account gives L ∝ M 3.5 . 6 How do astronomers know that the stars in globular clusters are old? The age of the cluster can be determined by the turn-off point of the main sequence on the HR diagram. Because: (a) The main-sequence age is proportional to stellar mass (b) The stellar mass is proportional to stellar luminosity (c) It follows that the cluster contains no higher-mass main-sequence star above this turn off. Therefore, the main-sequence age of the turn-off then tells us the age of the cluster. For globular cluster, this age is typically 1010 years; this is a large fraction of the age of the Universe (as we will learn in a few weeks).