Download R - FIU

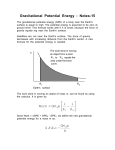
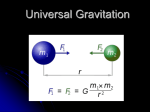
Chapter 13: Gravitation
•  Newton’s Law of Gravitation
•  Why is gravity important?
•  Revisit the following:
gravitational force, weight, and gravitational energy
•  Stellar motions: the orbits of satellites and celestial
objects
•  Black holes 101(beyond science fiction)
Introduction
•  Looking at the picture of Saturn, we
see a very organized ring around the
planet. Why do the particles arrange
themselves in such orderly fashion?
•  Gravity is the most important force
on the cosmo-level.
•  Why not strong/weak forces?
•  ElectroMagnetic(EM) force also
works at large distance? But is it
not as important?
Newton’s Law of Gravitation
•  The gravitational force is
always attractive and
depends on both the
masses of the bodies
involved and their
separations.
•  Everything attracts
everything else in the
universe
Gm1m2
r2
G = 6.67 × 10 −11 N • m 2 /kg 2
Fg =
So small! How was it measured?
€
Henry Cavendish determines G
•  Gravitational forces were relative until 1798 when Henry
Cavendish made the sensitive measurement to determine a
numerical value for the constant G.
Example of calculating gravitational forces
•  In the three stars shown below, that is the total gravitational force
Exerted on the small star at the origin?
F1 =
Gm0 m1
= 6.67 × 10 25 N
2
r1
2
6.67 × 10 25 N = 4.72 × 10 25 N
2
Gm0 m1
F2
r12
r22
=
=
F1 Gm0 m1 r22
r12
F1x = F1y =
r12
∴F2 = 2 F1 = 2F1 = 13.3 × 10 25 N
r2
Fx = 18.1 × 10 25 N
Fy = 4.72 × 10 25 N
€
Weight (skip Weight Watchers, just climb upward)
•  Gravity (and hence, weight) decreases as altitude rises.
Weight: Total gravitational force
from everything else in the universe!
In reality, only the nearest steller object matters!
w = Fg =
g=
€
Gmsteller _ object m
2
Rsteller
_ object
Gmsteller _ object
2
Rsteller
_ object
Q12.1
The mass of the Moon is 1/81 of the mass of the Earth. Compared to the gravitational force that the Earth exerts on the
Moon, the gravitational force that the Moon exerts on the Earth is
A. 812 = 6561 times greater. B. 81 times greater. C. equally strong. D. 1/81 as great.
E. (1/81)2 = 1/6561 as great.
A12.1
The mass of the Moon is 1/81 of the mass of the Earth. Compared to the gravitational force that the Earth exerts on the
Moon, the gravitational force that the Moon exerts on the Earth is
A. 812 = 6561 times greater. B. 81 times greater. C. equally strong. D. 1/81 as great.
E. (1/81)2 = 1/6561 as great.
Q12.3
Compared to the Earth, Planet X has twice the mass and twice
the radius. This means that compared to the Earth’s surface
gravity, the surface gravity on Planet X is A. 4 times as much. B. twice as much. C. the same.
D. 1/2 as much.
E. 1/4 as much.
A12.3
Compared to the Earth, Planet X has twice the mass and twice
the radius. This means that compared to the Earth’s surface
gravity, the surface gravity on Planet X is A. 4 times as much. B. twice as much. C. the same.
D. 1/2 as much.
E. 1/4 as much.
Gravitational potential energy
•  Objects changing their distance from earth are also
changing their potential energy with respect to earth.
w grav =
∫
r
(−
∞
GmmE
)dr = U ∞ − U(r)
2
r
GmmE r
∞ = U ∞ − U(r)
r
GmmE
= U ∞ − U(r)
r
Gmm E
U(r) = U ∞ −
In the
r
⇒
above plot, where did we choose
Is this consistent with U=mgh? the point where U=0?
€
Q12.4
Compared to the Earth, Planet X has twice the mass and twice
the radius. This means that compared to the amount of energy
required to move an object from the Earth’s surface to infinity,
the amount of energy required to move that same object from
Planet X’s surface to infinity is
A. 4 times as much. B. twice as much. C. the same.
D. 1/2 as much.
E. 1/4 as much.
A12.4
Compared to the Earth, Planet X has twice the mass and twice
the radius. This means that compared to the amount of energy
required to move an object from the Earth’s surface to infinity,
the amount of energy required to move that same object from
Planet X’s surface to infinity is
A. 4 times as much. B. twice as much. C. the same.
D. 1/2 as much.
E. 1/4 as much.
Q12.5
A satellite is moving around the Earth in a circular orbit.
Over the course of an orbit, the Earth’s gravitational force
A. does positive work on the satellite.
B. does negative work on the satellite.
C. does positive work on the satellite during part of the orbit
and negative work on the satellite during the other part.
D. does zero work on the satellite at all points in the orbit.
A12.5
A satellite is moving around the Earth in a circular orbit.
Over the course of an orbit, the Earth’s gravitational force
A. does positive work on the satellite.
B. does negative work on the satellite.
C. does positive work on the satellite during part of the orbit
and negative work on the satellite during the other part.
D. does zero work on the satellite at all points in the orbit.
What if you are inside the planet
g = 0@center
Boundary conditions
GM
g = 2 @surface
R
Can you guess what is g between r=0 and r=R?
Only the material below r would contribute:
The gravitational force at r from the center is only from the mass
inside the sphere with radius r (proof at section 12.6*)
4 3
Assuming the density
GM r Gρ ( 3 πr )
gr = 2 =
is constant
r
r2
4 3
 ρ( πR ) = M
3
r3
GM r GM( R 3 ) GM
∴gr = 2 =
= 3 r
2
r
r
R
€
The escape from earth, and the solar system: Minimum v
•  Example 12.5: What is a projectile’s velocity when launched, if it
could reach n times earth radius (RE)
•  The escape velocity/speed: escape from gravity and move to an
infinitely large distance (does the direction matter?)
R2=nRE
1
m m
m m
mv escape 2 + (−G E ) = 0 + (−G E )
2
RE
R∞
⇒ v escape = 2
1
m m
m m
mv 0 2 + (−G E ) = 0 + (−G E )
2
RE
nRE
⇒ v escape =
2(n −1)GmE
nRE
€
n →∝
GmE
RE
Can you guess what
is the escape velocity
from the solar system?
The escape from earth, and the solar system: Minimum v
•  Example 12.5: What is a projectile’s velocity when launched, if it
could reach n times earth radius (RE)
•  The escape velocity/speed: escape from gravity and move to an
infinitely large distance (does the direction matter?)
R2=nRE
1
m m
m m
mv escape 2 + (−G E ) = 0 + (−G E )
2
RE
R∞
⇒ v escape = 2
1
m m
m m
mv 0 2 + (−G E ) = 0 + (−G E )
2
RE
nRE
⇒ v escape =
2(n −1)GmE
nRE
€
n →∝
GmE
RE
The escape from earth, and the solar system: Minimum v
•  What is a projectile’s velocity when launched, if it could reach n
times earth radius (RE)
•  The escape velocity/speed: escape from gravity and move to an
infinitely large distance (does the direction matter?)
R2=nRE
1
m m
m m
mv escape 2 + (−G E ) = 0 + (−G E )
2
RE
R∞
⇒ v escape = 2
1
m m
m m
mv 0 2 + (−G E ) = 0 + (−G E )
2
RE
nRE
⇒ v escape =
2(n −1)GmE
nRE
GmE
RE
€
n →∝
sun
v escape
= 2
Gmsun
R0
€
Satellite motion
Do satellites always move in circles?
mE m
v2
G 2 =m
r
r
⇒
v= G
mE
r
T =?
K = ?U = ? E = ?
For every radius, there is only one speed that will
ensure the circular motion, independent of satellite mass
Synchronous satellite
•  Synchronous satellite: orbiting the earth at the same rate, direction
as the earth rotation; (T=24hrs, mE=5.97x1024kg, RE=6380km)
•  How high should it be from ground?
3
2
T=
2πr
GmE
T 2GmE 13
⇒ r =(
)
4π 2
Δr = r − RE
How much work needs to be done to move
the 1000kg satellite into orbit? Is it just the
increase of the potential energy?
w = ΔU + ΔK
Gmm E
Gmm E
ΔU = −
−(
)
r
RE
1 2 1 Gm E
ΔK = mv = m
2
2
r
Kepler’s laws for planetary motion:first law
•  Planet/Wanderer: We are
not the center of the world
•  Kepler’s first law:
Each planet moves in an
elliptical orbit with the sun
at one focus.
•  Why is it not always a
circle
Extreme cases: If the planet has a very large speed,
or it has just the right speed. In almost all cases, the
actual speed is somewhere in between
Kepler’s laws for planetary motion:second law
•  Kepler’s second law:
A line from the sun to a given
planet sweeps out equal areas in
equal times
•  What does this mean? Hint: What
is the angular momentum of the
planet?
1 2
dA 2 r dθ 1
dθ
1
1
=
= r(r ) = rv⊥ = rv sin φ
dt
dt
2
dt
2
2
L = r(mv)sin φ
•  Apparently, the planet’s angular
momentum doesn’t change.
Why?
€
Kepler’s laws for planetary motion:second law
•  Kepler’s second law:
A line from the sun to a given
planet sweeps out equal areas in
equal times
•  What does this mean? Hint: What
is the angular momentum of the
planet?
1 2
dA 2 r dθ 1
dθ
1
1
=
= r(r ) = rv⊥ = rv sin φ
dt
dt
2
dt
2
2
L = r(mv)sin φ
•  Apparently, the planet’s angular
momentum doesn’t change.
Why?
€
€
dL
 
=τ = r × F =0
dt
r, and F are in the same line!
Q12.6
A planet (P) is moving around the Sun
(S) in an elliptical orbit. As the planet
moves from aphelion to perihelion, the
Sun’s gravitational force
A. does positive work on the planet.
B. does negative work on the planet.
C. does positive work on the planet
during part of the motion and
negative work during the other part.
D. does zero work on the planet at
all points between aphelion and
perihelion.
A12.6
A planet (P) is moving around the Sun
(S) in an elliptical orbit. As the planet
moves from aphelion to perihelion, the
Sun’s gravitational force
A. does positive work on the planet.
B. does negative work on the planet.
C. does positive work on the planet
during part of the motion and
negative work during the other part.
D. does zero work on the planet at
all points between aphelion and
perihelion.
Q12.7
A planet (P) is moving around the Sun
(S) in an elliptical orbit. As the planet
moves from aphelion to perihelion, the
planet’s angular momentum
A. increases during part of the
motion and decreases during the
rest of the motion.
B. increases at all times. C. decreases at all times. D. remains the same at all times.
A12.7
A planet (P) is moving around the Sun
(S) in an elliptical orbit. As the planet
moves from aphelion to perihelion, the
planet’s angular momentum
A. increases during part of the
motion and decreases during the
rest of the motion.
B. increases at all times. C. decreases at all times. D. remains the same at all times.
Kepler’s laws for planetary motion:third law
•  Kepler’s third law:
3
2
2πa
The period of the planets are proportional
T=
to the 3/2 powers of the major axis lengths
GmE
of their orbits
We have already known this from the synchronous satellite (circular
Orbit). Why would this still be true€if the orbit is elliptical?
•  First and third law: Only valid when
1
Fg ∝ 2
r
•  Second law: As long as gravity is a central
force
€
•  How were the distances between planets
and stars measured then and now?
Halley’s comet
•  Why is Comet Halley so famous (Is it because it is the brightest)?
•  Knowing the comet return every 75.5 years (2.38x109 s), and the
sun’s mass is 1.99x1030kg, Can you deduce the semi-major axis
of its orbit
3
2
T=
2πa
GmS
T 2GmS 13
⇒ a=(
2 )
4π
Black hole 101
• What is a black hole?
• A black hole is formed when a star collapses due to its own
gravity, if the internal pressure could no longer be maintained via
nuclear reactions (fuel runs out)
• Black hole’s gravity is so large that even light can not escape
Try escape velocity being speed of light, and the minimum mass
is three times that of the sun: 3x(1.99x1030)kg
Event horizon
v escape
GmB
≡c = 2
RB
2GmB 2G(3mS )
⇒ RB =
=
2
c
c2
€
Wrong equation,
Correct result
Atoms sometimes are just like a solar system, with electrons
orbiting protons/neutrons, and lots of empty space in between?
What happens the atoms collapse and there
is no more empty space between the nucleons?
How to detect black holes
•  If light cannot escape black holes, how do we know we are there?
•  X-ray sources
•  Orbits of surrounding stars
Summary
Newton’s law of gravitation:
Gm1m2
r2
G = 6.67 × 10 −11 N • m 2 /kg 2
Fg =
Weight and gravitational€ potential energy
w = Fg =
g=
Compare this with U=mgh
Satellite in circular orbit:
v= G
mE
r
3
2
T=
2πr
GmE
€
Gmsteller _ object m
2
Rsteller
_ object
Gmsteller _ object
2
Rsteller
_ object
U =−
Gmsteller _ object
Rsteller _ object
When dealing with
steller objects, satellite,
we DON’t use U=mgh!
Kepler’s laws: Second law angular momentum conservation
€