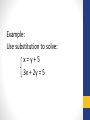Download File

Lesson 13:
Substitution, Area of
an Isosceles Triangle
Substitution Axiom:
If two expressions a and b are of equal
value, a = b, then a may replace b or b
may replace a in another expression
without changing the value of the
expression. Also, a may replace b or b
may replace a in any statement without
changing the truth or falsity of the
statement. Also, a may replace b or b may
replace a in any equation or inequality
without changing the solution set of the
equation or inequality.
Example:
Use substitution to solve:
x=y+5
3x + 2y = 5
Answer:
(3, -2)
Example:
Use substitution to solve:
3x – y = 11
2x + 3y = -11
Answer:
(2, -5)
Example:
Use substitution to solve:
x + y = 20
5x + 10y = 150
Answer:
(10, 10)
When we bisect an angle, we
divide the angle into two angles
whose measures are equal. When
we bisect a line segment, we divide
the line segment into two
segments whose lengths are equal.
Ray CD bisects angle ACB
We can find the altitude of an
isosceles triangle by drawing a line
segment that connects the midpoint
of the base to the opposite vertex.
Because one end of the segment is
the midpoint of a side the segment is
called a median. The median to the
base of an isosceles triangle is also a
perpendicular bisector of the base.
Example:
Find the area of this triangle.
Dimensions are in centimeters.
5
5
4
Answer:
2
2√21 cm
HW: Lesson 13 #1-30