Download Chapter 6: Probability and Simulation

Chapter 6:
Probability
The study of randomness
Warm-up
6.4 MATCHING PROBABILITIES Probability is a measure of
how likely an event is to occur.
Match one of the probabilities that follow with each
statement about an event. (The probability is usually a
much more exact measure of likelihood than is the verbal
statement.)
0, 0.01, 0.3, 0.6, 0.99, 1
(a) This event is impossible. It can never occur.
0
(b) This event is certain. It will occur on every trial of the
random phenomenon.
1
(c) This event is very unlikely, but it will occur once in a
while in a long sequence of trials.
0.01
(d) This event will occur more often than not.
0.6

6.8 THREE OF A KIND You read in a book on poker that
the probability of being dealt three of a kind in a fivecard poker hand is 1/50. Explain in simple language
what this means.

In the long run, of a large number of hands of five cards,
about 2% (one out of 50) will contain a three of a kind.
(Note: This probability is actually 88 /4165= 0.02113.)
6.1 The Idea of Probability
 Proportion
of heads to tails in a few tosses
will be erratic but after thousands of tosses
will approach the expected .5 probability
Random
- does not mean haphazard
- there are uncertain outcomes in the short
run, but there is a pattern in the long run
Ex: Random Digit Table
From one digit to the next there is no way to
tell what is going to be next, but in the table
as a whole you would expect
approximately 10% “0”, 10% “1”, 10% “2”,
etc…
Probability
- proportion of desired outcome in a large
number of repetitions
- long run relative frequency
- a number between 0 and 1
Short-run Regularity
o
Ex: Flipping a coin 6 times
o
Most people would think that H T H T T H is
more likely than T T T H H H but both are
equally likely.
o
Ex: Getting T T T T T does not make it any more
likely that you will get H on the next flip.
o
- Coins have no memory.
- Each flip is an independent event.
o
Streaks
o
If a basketball player makes several
consecutive shots, people will say he is more
likely to make his next shot because he is on a
streak.
o
This is not true because making 8 shots in a row
is no more likely than making 7 and missing 1.
o
Probability doesn’t show up in the short-run (one
game). The statistics come from a whole
lifetime of playing.
o
Players perform consistently, not in streaks.
Surprise Meeting
o
Running into someone in Times Square
that you haven’t seen in 10 years might
seem like a big coincidence.
o
But the average person has over 1500
acquaintances. The chance of running
into a particular one of them is small, but
running into any one of them is not that
small.
Law of Averages
o
If a couple already has 4 girls, should
there next child be a boy?
o
No, there is still a 50% chance of either.
o
In the long run (the population on the
planet) we expect about half girls, half
boys being born. But one family is a short
run.
Long Run
o
If you flip a coin and get T T T T T, you
won’t necessarily get H next. The law of
averages only works in the long run.
o
o
In the long run, if you flip a coin 10,000
times, you will get about 50% H/T, but
those first 5 T are overwhelmed by the
next 9,995 flips – the are not
“compensated” for.
6.2 Probability Models
 Probability


models have two parts:
A list of possible outcomes
A probability for each outcome.
Sample Space
 To
specify S we must state what
constitutes an individual outcome, then
which outcomes can occur (can be
simple or complex)


Ex: coin tossing, S = {H, T}
Ex: US Census: If we draw a random sample
of 50,000 US households, as the survey does,
the S contains all 50,000
Rolling two dice
 At
a casino- 36 possible outcomes when
we roll 2 dice and record the up-faces in
order (first die, second die)
 Gamblers
care only about number of dots
face up so the sample space for that is:

S = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
Techniques for
finding outcomes
 1.
Tree diagram
 For
tossing a coin
then rolling a die
 2.

 3.

Multiplication Principle
2x6 = 12 for same example
Organized list:
H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6
With/without replacement
 If
you take a card from a deck of 52,
don’t put it back, then draw your 2nd card
etc., that’s without replacement.

Ex: how many different 3 digit numbers can
you make: 10x9x8 = 720
 If
you take a card, write it down, put it
back, draw 2nd card etc., that’s with
replacement.

Ex: 10x10x10 = 1000
Probability Rules



1. Any probability is a number between 0 and 1
2. The sum of the probabilities of all possible outcomes
=1
3. If 2 events have no outcomes in common (they
can’t occur together), the probability that one OR the
other occurs is the sum of their individual probabilities


Ex: If one event occurs in 40% of all trials, another event
happens in 25% of all trials, the 2 can never occur
together, then one or the other occurs on 65% of all trials
4. The probability that an event doesn’t occur is 1
minus the probability that it does occur

Ex: If an event happens in 70% of all trials, it fails to occur
in the other 30%
Venn diagrams help!
Ex: Probability of rolling a 5?
B/c P(roll a 5 with 2 die) =
P(1,4) + P(3,2) + P(2,3) + P(4,1)
= 1/36 + 1/36 + 1/36 + 1/36
= 1/9 or .111
Independence &
the Multiplication Rule


To find the probability for BOTH events A and B
occurring
 Example: Suppose you plan to toss a coin twice, and
want to find the probability of rolling a head on both
tosses.
 A = first toss is a head, B = second toss is a head. So
(1/2)(1/2) = ¼. We expect to flip 2 heads on 25% of
all trials. The more times we repeat this, the closer our
average probability will get to 25%.
The multiplication rule applies only to independent
events; can’t use it if events are not independent!
Independent or not?

Coin toss


Drawing from deck of cards


I: Coin has no memory and coin tossers cannot
influence fall of coin
NI: First pick, probability of red is 26/52 or .5.
Once we see the first card is red, the probability
of a red card in the 2nd pick is now 25/51 = .49
Taking an IQ test twice in succession

NI
More applications of
Probability Rules
 If
two events A and B are independent,
then their complements are also
independent.

Ex: 75% of voters in a district are
Republicans. If an interviewer chooses 2
voters at random, the probability that the
first is a Republican and the 2nd is not a
republican is .75 x .25 = .1875
Homework
 11,
14, 15, 17, 18, 19, 20, 23 – 26, 27, 29-31,
33, 35, 37
6.3 General Probability Rules
Addition Rule for Disjoint events
General Addition rule for
Unions of 2 events
Example:

Deb and Matt are waiting anxiously to hear if
they’ve been promoted. Deb guesses her
probability of getting promoted is .7 and
Matt’s is .5, and both of them being
promoted is .3. The probability that at least
one is promoted = .7 + .5 - .3 which is .9. The
probability neither is promoted is .1.

The simultaneous occurrence of 2 events
(called a joint event, such as deb and matt
getting promoted) is called a joint probability.
Conditional Probability

The probability that we assign to an event
can change if we know some other event has
occurred.


P(A|B): Probability that event A will happen
under the condition that event B has occurred.
Ex: Probability of drawing an ace is 4/52 or 1/13.
If your are dealt 4 cards and one of them is an
ace, probability of getting an ace on the 5th
card dealt is 3/48 or 1/16 (conditional
probability- getting an Ace given that one was
dealt in the first 4).
In words, this says that for both of 2 events to occur,
first one must occur, and then, given that the first
event has occurred, the second must occur.
Remember: B is the event whose probability
we are computing and A represents the info
we are given.
Extended Multiplication rules
 The
union of a collection of events is the
event that ANY of them occur
 The Intersection of any collection of
events is the event that ALL of them occur
Example

Only 5% of male high school basketball, baseball, and football
players go on to play at the college level. Of these only 1.7%
enter major league professional sports. About 40% of the
athletes who compete in college and then reach the pros have
a career of more than 3 years. Define these events:





A = competes in college
years
P(A) = .05
P(B|A) = .017
P(C|A and B) = .400
What is the probability a HS athlete will have a pro career more
than 3 years? The probability we want is therefore



B = competes pro C = pro career longer than 3
P(A and B and C) = P(A)P(B|A)P(C|A and B)
= .05 x .017 x .40 = .00034
So, only 3 of every 10,000 high school athletes can expect to
compete in college and have a pro career of more than 3 years.
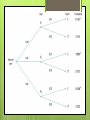
Extended tree diagram + chat
room example


47% of 18 to 29 age chat online, 21% of 30 to 49
and 7% of 50+
Also, need to know that 29% of all internet users
are 18-29 (event A1), 47% are 30 to 49 (A2) and
the remaining 24% are 50 and over (A3).



What is the probability that a randomly chosen
user of the internet participates in chat rooms
(event C)?
Tree diagram- probability written on each
segment is the conditional probability of an
internet user following that segment, given that he
or she has reached the node from which it
branches.
(final outcome is adding all the chatting
probabilities which = .2518)
Bayes Rule

Another question we might ask- what percent of
adult chat room participants are age 18 to 29?

P(A1|C) = P(A1 and C) / P(C)
= .1363/.2518 = .5413
*since 29% of internet users are 18-29, knowing that
someone chats increases the probability that they
are young!
Formula sans tree diagram:
P(C) = P(A1)P(C|A1) + P(A2)P(C|A2) + P(A3)P(C|A3)
6.3 Need to Know summary(print)









Complement of an event A contains all outcomes not in A
Union (A U B) of events A and B = all outcomes in A, in B, or in
both A and B
Intersection(A^B) contains all outcomes that are in both A and
B, but not in A alone or B alone.
General Addition Rule: P(AUB) = P(A) + P(B) – P(A^B)
Multiplication Rule: P(A^B) = P(A)P(B|A)
Conditional Probability P(B|A) of an event B, given that event A
has occurred: P(B|A) = P(A^B)/P(A) when P(A) > 0
If A and B are disjoint (mutually exclusive) then P(A^B) = 0 and
P(AUB) = P(A) + P(B)
A and B are independent when P(B|A) = P(B)
Venn diagram or tree diagrams useful for organization.