* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download a R
Survey
Document related concepts
Transcript
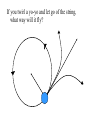
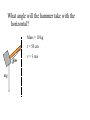
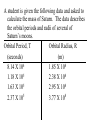
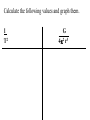
Circular Motion and Gravitation Centripetal Acceleration – acceleration towards the center of a circle. – a.k.a. Radial Acceleration (aR) v Ball rolling in a straight line (inertia) v aR aR Same ball, hooked to a string v aR = 2 v r If you are on a carousel at constant speed, are you experiencing acceleration? If you twirl a yo-yo and let go of the string, what way will it fly? Period and Frequency Period (T) – Time for one complete (360o) revolution – seconds Frequency – Number of revolutions per second – rev/s or Hertz (Hz) T=1 f Formulas aR = v2 r v = 2pr T T=1 f v = 2prf Centripetal Acceleration: Ex. 1 A 150-g ball is twirled at the end of a 0.600 m string. It makes 2.00 revolutions per second. Find the period, velocity, and acceleration. (0.500 s, 7.54 m/s, 94.8 m/s2) Centripetal Acceleration: Ex. 2 The moon has a radius with the earth of about 384,000 km and a period of 27.3 days. a. Calculate the acceleration of the moon toward the earth. b. Convert the answer to g’s. (Ans: 2.72 X 10-3 m/s2, 2.78 X 10-4 g ) Jupiter is about 778 X 106 km from the sun. It takes 4332.6 days to orbit the sun. a) Calculate the circumference of Jupiter’s . orbit. (4.89 X 1012 m) b) Calculate Jupiter’s period in seconds. (3.74 X 108 s) c) Calculate Jupiter’s orbital speed. (1.30 X 104 m/s) d) Calculate Jupiter’s centripetal acceleration towards the sun. (2.18 X 10-4 m/s2) Centripetal Force Centripetal Force – “center seeking” force that pulls an object in a circular path. – – – – Yo-yo Planets Merry-go-round Car rounding a curve? “Centrifugal Force?” • Doesn’t exist • “apparent outward force” • When you let the string go, the ball will continue in a straight line path. No new acceleration involved. • Water in swinging cup example Direction water wants to go Centripetal Force of string Circular Motion SF = maR = mv2 r A 0.150 kg yo-yo is attached to a 0.600 m string and twirled at 2 revolutions per second. a) Calculate the circumference of the circle (3.77 m) b) Calculate the linear speed (7.54 m/s) c) Calculate the centripetal force in the string (14.2 N) An electron orbits the nucleus with a radius of 0.5 X 10-10 m. The electron has a mass of 9 X 10-31 kg and a speed of 2.3 X 106 m/s. a. Calculate the centripetal force on the electron. (9.52 X 10-8 N) b. Calculate the frequency of an electron. (7.32 X 1015 Hz) c. Convert the velocity to miles/s. (1429 miles/s) d. What provides the centripetal force? Circular Motion: Example 2 Thor’s Hammer (mjolnir) has a mass of 10 kg and the handle and loop have a length of 50 cm. If he can swing the hammer at a speed of 3 m/s, what force is exerted on Thor’s hands? (Ans: 180 N) Can Thor swing his hammer so that it is perfectly parallel to the ground? FH What angle will the hammer take with the horizontal? Mass = 10 kg r = 50 cm q mg v = 3 m/s What angle will the hammer take with the horizontal? Let’s resolve the FR vector into it’s components: FHx = Fhcosq q FHx = mv2/r FHcosq = mv2/r mg SFy = 0 (the hammer is not rising or falling) 0 = FHsinq – mg Two Equations: Two Unknowns FHcosq = mv2/r FHsinq = mg FH = mv2 rcosq mv2 sinq = mg r cosq sinq = gr cosq v2 tan q = gr v2 q = 28.6o A 0.0050 kg walnut is swung in a radius of 50.0 cm. The walnut makes 2.50 revolutions per second. a) Calculate the linear speed of the walnut. (7.85 m/s) b) Draw a free-body diagram of the walnut. c) Calculate the centripetal force needed to keep it in a circle. (0.616 N) d) Calculate the force of tension and the angle the string makes with the horizontal. (0.618 N, 4.5o) Circular Motion: Example 3 A 0.150 kg ball is swung on a 1.10-m string in a vertical circle. What minimum speed must it have at the top of the circle to keep moving in a circle? mg FT At the top of the circle, both the weight and the tension in the string contribute to the centripetal force SF = FT + mg v = 3.28 m/s What is the tension in the cord at the bottom of the arc if the ball moves at the minimum speed? (v = 3.28 m/s) FT = 2.94 N FT mg A rollercoaster vertical loop has a radius of 20.0 m. Assume the coaster train has a mass of 3,000 kg. a) Calculate the minimum speed the coaster needs to have to make the loop. (14.0 m/s) b) Calculate the normal force the tracks provide to the train at the bottom of the curve if the train is travelling at 25.0 m/s. (123,150 N) c) Calculate the normal force the tracks provide at the top of the curve if the train is travelling at 25.0 m/s. (64, 350 N) The ferris wheel at Knoebels has a radius of 16.8 m and travels at a speed of 3.52 m/s. a) Calculate the frequency and period (0.033 Hz, 30 s) b) Calculate the normal force that the seat provides to a 56.0 kg rider at the top. (507 N) c) Calculate the normal force that the seat provides to a 56.0 kg rider at the bottom. (590 N) A car travels over a round hill (radius = 50.0 m). a) Calculate the maximum speed at which the car can take the hill. (22.0 m/s) b) Calculate the normal force on a 1000.0 kg car if it is travelling over the hill at 10.0 m/s. (7.80 X 103 N) Car Rounding a Turn • Friction provides centripetal force • Use (ms). Wheels are turning, not sliding, across the surface • Wheel lock = kinetic friction takes over. mk is always less than ms, so the car is much more likely to skid. Car Rounding a Turn: Example 1 A 1000-kg car rounds a curve (r=50 m) at a speed of 14 m/s. FN Ffr = Fc mg a) Calculate the centripetal force needed to keep the car on the road b) Calculate if the car will skid if the road is dry and ms = 0.60 c) Calculate if the car will skid if the road is icy and ms = 0.25 Car Rounding a Turn: Example 2 A 15,000-kg truck can safely round a 150 m curve at a speed of 20 m/s. a) Calculate the centripetal force needed to keep the car on the road (40,000 N ) b) Calculate the coefficient of static friction (0.27) c) Calculate the maximum speed a 1000 kg Cube car can take the turn. (20 m/s) The Rotor The Rotor at an amusement park has a radius of 7.0 m and makes 30 rev/min. a) Calculate the speed of the rotor. ( 22.0 m/s) b) Draw a free body diagram of a person in the rotor. What causes the FN? c) Calculate the coefficient of static friction between the person and the wall. (0.14) Banked Curves • Banked to reduce the reliance on friction • Part of the Normal Force now contributes to the centripetal force FC = Ffr + FNsinq (ideally, we bank the road so that no friction is required: Ffr = 0) Banked Curves: Example 1 A 1000-kg car rounds a 50 m radius turn at 14 m/s. What angle should the road be banked so that no friction is required? FN q mg q Now we will simply work with the Normal Force to find the component that points to the center of the circle First consider the y forces. SFy = FNcosq - mg Since the car does not move up or down: FNcosq FN q SFy = 0 FNsinq 0 = FNcosq – mg FNcosq = mg q mg q FN = mg/cosq mv2 = FNsinq r mv2 = mgsinq r cosq v2 = gtanq r v2 = gtanq r v2 = tanq gr tan q = q = 22o (14 m/s)2 (50 m)(9.8m/s2) = 0.40 A 2,000-kg Nascar car rounds a 300 m radius turn at 200 miles/hr. a. Convert the speed to m/s. (89.4 m/s) b. What angle should the road be banked so that no friction is required? (70o) c. Suppose a track is only banked at 35.0o, calculate the maximum speed that a car can take the turn. (45.3 m/s, 101 mph) d. Looking at the formula for banking angle, how could a track designer decrease that angle? Weightlessness • True weightlessness exists only very far from planets • “Apparent weightlessness” can be achieved on earth Elevator at Constant Velocity a= 0 SF = FN – mg 0 = FN – mg FN = mg Suppose Chewbacca has a mass of 102 kg: FN = mg = (102kg)(9.8m/s2) FN = 1000 N FN mg a is zero Elevator Accelerating Upward a = 4.9 m/s2 SF = FN – mg ma = FN – mg FN = ma + mg FN = m(a + g) FN=(102kg)(4.9m/s2+9.8 m/s2) FN = 1500 N FN mg a is upward Elevator Accelerating Downward a = 4.9 m/s2 SF = mg - FN ma = mg - FN FN = mg - ma FN = m(g - a) FN=(102kg)(9.8m/s2 – 4.9 m/s2) FN = 500 N FN mg a is down At what acceleration will he feel weightless? FN = 0 SF = mg - FN ma = mg -FN ma = mg - 0 ma = mg a = 9.8 m/s2 Apparent weightlessness occurs if a > g FN mg Calculate the apparent weight of a 56.0 kg man in an elevator if the elevator is: a) Accelerating upwards at 2.00 m/s2. (661 N) b) Accelerating downwards at 2.00 m/s2 (436 N) c) Accelerating downwards at 9.80 m/s2 (0 N) d) Accelerating sideways at 9.80 m/s2. (549 N) Other examples of apparent weightlessness Even when you are running, you fell weightless between strides. Why don’t satellites fall back onto the earth? • Speed • They are “falling” due to the pull of gravity • Can feel “weightless” (just like in the elevator) Gravitation Is gravity caused by the earth’s rotation? Will a man down here fall off if the earth stops rotating? Gravitation Newton’s Law of Universal Gravitation 1. Every object in the universe is attracted to every other object. (based on mass) 2. The force drops off with the distance squared. (As distance increases, the force of gravity drops very quickly) Gravitation: Formula F= Gm1m2 r2 G = 6.67 X 10-11 N-m2/kg2 m1 = mass of one object m2 = mass of second object r = distance from center of objects Cavendish proves the law in 1798 Gravitation: The Solar System Everything in the solar system pulls on everything else. Sun pulls on Earth All the other planets also pull on the Earth Some comets/meteors are actually from outside our solar system and were captured by our sun’s gravity. Gravitation: Example 1 What is the force of gravity between two 60.0 kg (132 lbs) people who standing 2.00 m apart? F= Gm1m2 = (6.67 X 10-11 N-m2/kg2)(60kg)(60kg) r2 (2.00m)2 F = 6.00 X 10-8 N Such a force is so small that it is almost impossible to measure. Gravitation: Example 2 What is the force of gravity between a 60 kg person and the earth? Assume the earth has a mass of 5.98 X 1024 kg and a radius of 6,400,000 m (4,000 miles). F= Gm1m2 = (6.67 X 10-11 N m2/kg2)(60kg)(5.98 X 1024 kg) r2 (6,400,00 m)2 F = 584 N Gravitation: Example 3 A 2000-kg satellite orbits the earth at an altitude of 6380 km (the radius of the earth)above the earth’s surface. What is the force of gravity on the satellite? F= Gm1m2 = (6.67 X 10-11 N m2/kg2)(2000kg)(5.98 X 1024 kg) r2 (6,380,00 m + 6,380,00 m)2 F = 4900 N Gravitation: Example 3 What is the net force on the moon when it is at a right angle with the sun and the earth? Relevant Data: MM = 7.35 X 1022 kg ME = 5.98 X 1024 kg MS = 1.99 X 1030 kg rMS = 1.50 X 1011 m rME = 3.84 X 108 m Calculate each force separately: FME Earth 1020 N FME = 1.99 X FMS = 4.34 X 1020 N FR2 = FME2 + FMS2 q FMS FR = 4.77 X 1020 N tan q = opp = FME adj FMS q = 24.6o Sun FR Calculating the Mass of the Earth Calculate the mass of the earth knowing that it has a radius of 6.38 X 106 m. Start using the weight formula. Calculating “g” g = GmE rE 2 g = (6.67 X 10-11 N-m2/kg2)(5.98 X 1024 kg) (6.38 X 106 m)2 g = 9.80 m/s2 Calculating “g”: Example 1 Calculate the value of g at the top of Mt. Everest, 8848 m above the earth’s surface. g = GmE r2 g = (6.67 X 10-11 N-m2/kg2)(5.98 X 1024 kg) (6.38 X 106 m + 8848 m)2 g = 9.77 m/s2 g varies with: • Altitude • Location – Earth is not a perfect sphere – Different mineral deposits can change density – “salt domes” are low density salt regions near petroleum deposits Objects weigh about 1/6 their weight on Earth on the Moon. Calculate the mass of the moon, knowing that the radius of the moon is 1734 km. An object weighs 200 N on earth. a) Calculate the acceleration of gravity on Mars (3.71 m/s2) b) Calculate its weight on Mars (75.5 N) Re = 6370 km Rm = 3440 km Me = 5.98 X 1024 kg Mm = 0.11Me Three 5.00 kg bowling balls are placed at the corners of an equilateral triangle whose sides are 1.50 m long. Calculate the magnitude and direction of the gravitational force on the top ball. Four 5.00 kg bowling balls are placed at the corners of an square whose sides are 1.50 m long. Calculate the magnitude and direction of the gravitational force on the lower left ball. (1.42 X 10-9 N, 45o) A geosynchronous satellite has a period of one day. The radius of the Earth is 6380 km and the mass of the Earth is 5.98 X 1024 kg. a) Convert the period to seconds (8.64 X 104 s) b) Calculate the height above the earth that a geosynchronous satellite must orbit. (Hint: use mv2/r , and subtract the radius of the earth) (3.59 X7 m) c) Calculate the speed of the orbit. (3070 m/s) A satellite orbits with a period of 5.00 hours. The radius of the Earth is 6380 km and the mass of the Earth is 5.98 X 1024 kg. a) Calculate the height of the satellite above the earth. (8.47 X 106 m) b) Calculate the speed of the orbit. (5.183X103 m/s) Kepler’s Laws (1571-1630) 1. The orbit of each planet is an ellipse, with the sun at one focus 2. Each planet sweeps out equal areas in equal time 3. T12 = r13 T22 r23 1. The orbit of each planet is an ellipse, with the sun at one focus 2. Each planet sweeps out equal areas in equal time • Suppose the travel time in both cases is three days. • Shaded areas are exactly the same area The Third Law: Example 1 Mars has a year that is about 1.88 earth years. What is the distance from Mars to the Sun, using the Earth as a reference (rES = 1.496 X 108 m) T12 = r13 T22 r23 TM2 = rM3 TE2 rE3 rM3 = TM2rE3 TE2 rM3 = (1.88y)2(1.496 X 108 m)3 (1 y)2 rM3 = 1.18 X 1025 m3 rM = 2.28 X 108 m Third Law: Example 2 How long is a year on Jupiter if Jupiter is 5.2 times farther from the Sun than the earth? TJ2 = rJ3 TE 2 r E 3 TJ2 = rJ3 TE2 rE 3 TJ2 = rJ3 TE2 = (5.2)3(1 y)2 rE 3 (1)3 TJ2 = 141 y2 TJ = 11.9 y Third Law: Example 3 How high should a geosynchronous satellite be placed above the earth? Assume the satellite’s period is 1 day, and compare it to the moon, whose period is 27 days. The average distance between the earth and the moon is 384,000 km. Ts2 = rs3 TM2 rM3 rs3 = rM3 Ts2 TM2 rs3 = rM3 Ts2 TM2 rS3 = rM3 729 = rM3 (1 day)2 (27 day)2 Take the 3rd root of both sides rs = rM 9 The satellite must orbit 1/9 the distance to the moon. (4.27 X 107 m) Deriving the Third Law To derive Kepler’s Law, we will need two formulas. F= Gm1mJ r2 mJ m1 F=m1v2 r Gm1mJ = m1v2 r2 r GmJ = v2 r GmJ = 4p2r2 r T2 T2 = 4p2 r3 GmJ Substitute v=2pr T T2 = 4p2 r3 GmJ T12 = 4p2 r13 GmJ T12 = T22 r13 r23 We can do this for two different moons T22 = 4p2 r23 GmJ A Useful Form This form of the equation: S could be the Sun, Earth, or other body with satellites. T2 = 4p2 r3 GmS (solve it for ms) Useful for determining the mass of the central planet, using only the period and distance of one of the satellites. Third Law: Example 4 What is the mass of the sun, knowing that the earth is 1.496 X 1011 m from the sun. T2 = 4p2 r3 GmS mS= 4p2r3 GT2 mS= 4p2(1.496 X 1011 m)3 (6.67 X 10-11 N-m2/kg2) (3.16 X 107 s)2 mS = 2.0 X 1030 kg Calculate the mass of Neptune if you know that the period of its moon Galatea is 0.429 days, and the radius is 61,953 km from the center of Neptune. (1.02 X 1026 kg) The Gemini 11 spacecraft sent two astronauts to a height of 1374 km above the earth’s surface. The radius of the Earth is 6380 km and the mass of the Earth is 5.98 X 1024 kg. a) Calculate the speed of the orbit. (7173 m/s) b) Calculate the period of the satellite (1.89 hour) The mass of Mars is 6.40 X 1023 kg. Calculate the period of its moon Phobos if Phobos has an orbital radius of 9377 km. (7.67 h) Pluto has a radius of 1150 km and a mass of 1.20 X 1022 kg. a) Calculate the acceleration of gravity on Pluto (0.605 m/s2) b) Calculate the weight of a 70.0 kg person on Pluto. (42.4 N) c) Calculate the acceleration of gravity on Pluto in terms of “g’s” (0.0618 g’s) A student is given the following data and asked to calculate the mass of Saturn. The data describes the orbital periods and radii of several of Saturn’s moons. Orbital Period, T Orbital Radius, R (seconds) (m) 8.14 X 104 1.85 X 108 1.18 X 105 2.38 X 108 1.63 X 105 2.95 X 108 2.37 X 105 3.77 X 108 Let’s use this equation: T2 = 4p2 r3 GmS And rearrange it: GmS= 1 4p2 r3 T2 Once more: 1 = GmS T2 4p2 r3 Calculate the following values and graph them. 1 T2 G 4p2 r3 1.60E-10 1.40E-10 1.20E-10 1.00E-10 8.00E-11 6.00E-11 4.00E-11 2.00E-11 0.00E+00 0.00E+00 5.00E-38 1.00E-37 1.50E-37 2.00E-37 2.50E-37 3.00E-37 Calculate the slope of the graph y = m x 1 = mS G T2 4p2 r3 ms = 5.9 X 1026 kg +b The Four Fundamental Forces 1. 2. 3. 4. Gravity Electromagnetic Strong Nuclear Force Weak Nuclear Force 2. a) 1.52 m/s2, center b) 38.0 N, center 4.12 m/s 6.14 m/s, no effect 8.a) 3.14 N b) 9.02 N 10. 27.6 m/s, 0.439 rev/s 12. 9.2 m/s 14. 11 rev/min 16.FT1 = 4p2f2(m1r1 + m2r2) FT2 = 4p2f2m2r2 18. 0.20 26. 1.62 m/s2 28. 24.5 m/s2 30. 0.91 gsurface 32. 2.0 X 107 m 34. a) 9.8 m/s2 b) 4.3 m/s2 36. 9.6 X 1017 N away from the Sun 38. 2.0 X 1030 kg 40. 3.14 m/s2 upward 42. 5.07 X 103 s (1.41 h), independent of mass 44.a) 58 kg b) 58 kg c) 77 kg d) 39 kg e) 0 44.a) 58 kg (569N) b) 58 kg(569N) c) 77 kg (755 N) d) 39 kg (382N) e) 0 52. RIcarus = 1.62 X 1011 m 54. 5.97 X 1024 kg 56. 3.4 X 1041 kg, 1.7 X 1011 “Suns” 58.REuropa = 6.71 X 105 km RGanymede = 1.07 X 106 km RCallisto = 1.88 X 106 km 68.1840 rev/day 70. a) 3000 m b) 5500 N c) 3900 N Graphing Centripetal Force A A 1 kg yo-yo was swung in a circle at a constant speed. The force on the string was measured as the string was let out slowly. Radius (m) 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 Force (N) 10.00 5.00 3.33 2.50 2.00 1.67 1.43 1.25 1.11 1.00 Graphing Centripetal Force B In a second experiment, the speed was changed while the length of the string (r) was kept constant Speed (m/s) 1.0 2.0 3.0 4.0 5.0 6.0 Force (N) 1.0 4.0 9.0 16 25 36