Download k - CSE, IIT Bombay

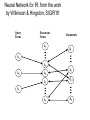
CS621 : Artificial Intelligence
Pushpak Bhattacharyya
CSE Dept.,
IIT Bombay
Lecture 25: Backpropagation and NN based IR
Backpropagation algorithm
j
wji
i
….
….
….
….
Output layer
(m o/p neurons)
Hidden layers
Input layer
(n i/p neurons)
• Fully connected feed forward network
• Pure FF network (no jumping of connections
over layers)
Gradient Descent Equations
E
w ji  
(  learning rate, 0    1)
w ji
E
E net j


(net j  input at the jth neuron )
w ji net j w ji
E
 j
net j
net j
w ji  j
w ji
w ji  joi
Backpropagation – for
outermost layer
E
E o j
j  


(net j  input at the jth neuron )
net j
o j net j
1 m
E   (t p  o p ) 2
2 p 1
Hence, j  ((t j  o j )o j (1  o j ))
w ji   (t j  o j )o j (1  o j )oi
Backpropagation for hidden
layers
k
j
i
….
….
….
….
Output layer
(m o/p neurons)
Hidden layers
Input layer
(n i/p neurons)
k is propagated backwards to find value of j
Backpropagation – for hidden
layers
w ji  joi
o j
E
E
j  


net j
o j net j
E

 o j (1  o j )
o j
E
netk
  (

)  o j (1  o j )
o j
knext layer net k
Hence,  j  

 (w
knext layer
kj
 (
knext layer
k
 wkj )  o j (1  o j )
 k )o j (1  o j )oi
General Backpropagation Rule
• General weight updating rule:
w ji  joi
• Where
 j  (t j  o j )o j (1  o j )

 (w 
knext layer
kj
k
for outermost layer
)o j (1  o j )oi for hidden layers
Issues in the training algorithm
•
•
•
•
Greedy Algorithm
Always changes weight such that E reduces.
The algorithm may get stuck up in a local minimum.
If we observe that E is not getting reduced anymore,
the following may be the reasons:
Issues in the training algorithm
contd.
1. Stuck in local minimum.
2. Network paralysis. (High –ve or +ve i/p makes
neurons to saturate.)
3.  (learning rate) is too small.
Diagnostics in action (1)
1) If stuck in local minimum, try the following:
• Re-initializing the weight vector.
• Increase the learning rate.
• Introduce more neurons in the hidden layer.
Diagnostics in action (2)
2) Observe the outputs: If they are close to 0 or 1,
try the following:
1. Scale the inputs or divide by a normalizing
factor.
2. Change the shape and size of the sigmoid.
Kolmogorov Statement pertaining
to Hidden Layer Design
Kolgomorov statement:
A feedforward network with three layers (input,
output and hidden) with appropriate I/O relation
that can vary from neuron to neuron is sufficient to
compute any function.
 However, More hidden layers reduce the size of
individual layers.
Momentum factor
1. To increase speed of learning Introduce momentum
factor 
(w ji ) nth  iteration  jOi   (wji)( n  1)th  iteration
 Accelerates the movement out of the trough.
 Dampens the oscillation inside the trough.
 Choosing : If  is large, we may jump over the
global minimum.
An application in Medical
Domain
Expert System for Skin Diseases
Diagnosis
• Bumpiness and scaliness of skin
• Mostly for symptom gathering and for
developing diagnosis skills
• Not replacing doctor’s diagnosis
Architecture of the FF NN
• 96-20-10
• 96 input neurons, 20 hidden layer neurons, 10 output
neurons
• Inputs: skin disease symptoms and their parameters
– Location, distribution, shape, arrangement, pattern,
number of lesions, presence of an active norder,
amount of scale, elevation of papuls, color, altered
pigmentation, itching, pustules, lymphadenopathy,
palmer thickening, results of microscopic
examination, presence of herald path, result of
dermatology test called KOH
Output
• 10 neurons indicative of the diseases:
– psoriasis, pityriasis rubra pilaris, lichen
planus, pityriasis rosea, tinea versicolor,
dermatophytosis, cutaneous T-cell lymphoma,
secondery syphilis, chronic contact dermatitis,
soberrheic dermatitis
Training data
• Input specs of 10 model diseases from 250
patients
• 0.5 if some specific symptom value is not known
• Trained using standard error backpropagation
algorithm
Testing
• Previously unused symptom and disease data of 99 patients
• Correct diagnosis achieved for 70% of papulosquamous group skin
diseases
• Success rate above 80% for the remaining diseases except for
psoriasis
• psoriasis diagnosed correctly only in 30% of the cases
• Psoriasis resembles other diseases within the papulosquamous
group of diseases, and is somewhat difficult even for specialists to
recognise.
Explanation capability
• Rule based systems reveal the explicit path of
reasoning through the textual statements
• Connectionist expert systems reach conclusions
through complex, non linear and simultaneous
interaction of many units
• Analysing the effect of a single input or a single
group of inputs would be difficult and would yield
incor6rect results
Explanation contd.
• The hidden layer re-represents the data
• Outputs of hidden neurons are neither symtoms
nor decisions
Duration
of lesions : weeks
Duration
of lesions : weeks
Symptoms & parameters
0
Internal
representation
Disease
diagnosis
0
1
0
( Psoriasis node )
Minimal itching
6
Positive
KOH test
Lesions located
on feet
1.68
10
13
5
(Dermatophytosis node)
1.62
36
14
Minimal
increase
in pigmentation 71
1
Positive test for
pseudohyphae
95
And spores
19
Bias
Bias
96
9
(Seborrheic dermatitis node)
20
Figure : Explanation of dermatophytosis diagnosis using the DESKNET expert system.
Discussion
• Symptoms and parameters contributing to the
diagnosis found from the n/w
• Standard deviation, mean and other tests of
significance used to arrive at the importance of
contributing parameters
• The n/w acts as apprentice to the expert
Neural Network for IR
Slides taken from lecture notes material accompanying
the book Modern Information Retrieval, Ricardo Baeza
Yates
Neural Network for IR: from the work
by Wilkinson & Hingston, SIGIR’91
Query
Terms
Document
Terms
k1
Documents
d1
ka
ka
kb
kb
kc
dj
dj+1
kc
kt
dN
Three layers network
• Query terms issue the first inputs
– These inputs propagate accross the
network to reach the document nodes
• Second level of propagation:
– Document nodes might themselves
generate new iputs which affect the
document term nodes
– Document term nodes might respond with
new inputs of their own
Weight Assignments
• Weight associated with an edge from a query term
node ki to a document term node ki
Wiq  wiq

t
2
iq
w
i 1
Next layer weight assignment
• Weight associated with an edge from a document
term node ki to a document node dj:
Wij  wij

t
2
ij
w
i 1
Document Ranking
• After the first level of input propagation, the
activation level of a document node dj is given by:
Wiq .Wij  i 1 wiq wij
t
i1 w *
t
2
iq
2
w
i1 ij
t
which is exactly the ranking of the Vector model
The feedback has the effect of thesaurus based expansion
Terrier Assignment
• corpus link
• http://www.cfilt.iitb.ac.in/~ashish/irasgn/trec_wsj_
1989.tar.gz
• 50 topics link
• http://www.cfilt.iitb.ac.in/~ashish/irasgn/topics.ws
j.150-200