Download الوحدة العاشرة

1
Systems
of
Linear Algebraic
Equations Part Three
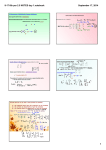
Definition (Band Matrix)
A n×n square matrix A is called a band matrix if
there exists positive integers p and q, with 1 < p
and q < n such that
aij = 0 for p ≤ j − i or q ≤ i − j.
02
 a11
a
 21
a31
A
a41
a51

a61
a12 a13 a14 a15 a16 

a22 a23 a24 a25 a26 
a32 a33 a34 a35 a36 

a42 a43 a44 a45 a46 
a52 a53 a54 a55 a56 

a62 a63 a64 a65 a66 
p 1
p2
qn
q4
aij  0 for 2  j  i
aij  0 for 4  i  j
20
Definition (Band Matrix)
The number p describes the number of diagonals
above, and including, the main diagonal on which
nonzero entries may lie.
The number q describes the number of diagonals
below, and including, the main diagonal on which
nonzero entries may lie.
03
Definition (Band Matrix)
The number p + q − 1 is called the bandwidth of
the matrix A, which tells us how many of the
diagonals can contain nonzero entries.
For example, the following matrix
04
Definition (Band Matrix)
the following matrix
is banded with p = 3 and q = 2, and so the
bandwidth is equal to 4.
05
Definition (Band Matrix)
An important property of the band matrix is called
the tridiagonal matrix, in this case p = q = 2, that is,
all nonzero elements lie either on or directly above
or below the main diagonal.
06
Definition (Band Matrix)
For such type of matrix, the Gaussian elimination
is particular simpler.
In general, the nonzero elements of a tridiagonal
matrix lie in three bands:
the superdiagonal, diagonal and subdiagonal.
07
Definition (Band Matrix)
For example,
is a tridiagonal matrix.
1 2

2 3 1



 3 2 2

A

2
4
3



1 2 3


3
4


A matrix which is predominantly zero is called a
sparse matrix.
A band matrix or a tridiagonal matrix is a sparse
matrix but the nonzero elements of a sparse matrix
are not necessarily near the diagonal.
08
The Determinant of Matrix
The determinant is a certain kind of a function that
associates a real number with a square matrix.
We will denote the determinant of a square matrix
A by det(A) or |A|.
09
Definition (Determinant of Matrix
)
Let A = (aij) be an n × n square matrix then a
determinant of A is given by:
1. det(A) = a11 ,
if n = 1.
2. det(A) = a11a22 − a12a21, if n = 2.
10
Notice that the determinant of a 2 × 2 matrix is
given by the difference of the products of the two
diagonals of a matrix.
The determinant of a 3 × 3 matrix is defined in
terms of determinants of 2 × 2 matrices and the
determinant of a 4 × 4 matrix is defined in terms of
determinants of 3 × 3 matrices and so on.
11
Other way to find the determinants of only 2 × 2 and
3 × 3 matrices can be found easily and quickly using
diagonals (or direct evaluation).
For 2 × 2 matrix, the determinant can be obtained
by forming the product of the entries on the line
from left to right and subtracting from this number
the product of the entries on the line from right to
left.
12
For a matrix of size 3×3 , the diagonals of an array
consisting of the matrix with the two first columns
added to the right are used.
Then the determinant can be obtained by forming
the sum of the products of the entries on the lines
from left to right, and subtract from this number
the products of the entries on the lines from right to
left, as shown in Figure.
13
14
Thus for 2 × 2 matrix
|A| = a11a22 − a12a21,
and for 3 × 3 matrix
|A| = a11a22a33 + a12a23a31 + a13a21a32
− a13a22a31 − a11a23a32 − a12a21a33
(diagonal products from left to right)
(diagonal products from right to left)
For finding the determinants of the higher-order
matrices, we will define the following concepts of
minor and cofactor of the matrices.
15
Definition (Minors of a Matrix)
The minor Mij of all elements aij of a matrix A of
order n×n as the determinant of the sub-matrix of
order (n − 1) × (n − 1) obtained from A by deleting
the ith row and jth column (also called ijth minor
of A).
16
Definition (Cofactor of a Matrix)
The cofactor Aij of all elements aij of a matrix A of
order n × n is given by
i+j
Aij = (−1) Mij ,
where Mij is the minor of all elements aij of a matrix
A.
17
Definition (Cofactor Expansion of Determinant of a Matrix)
Let A be a square matrix, then we define
determinant of A is the sum of the products of the
elements of the first row and their cofactors.
If A is 3 × 3 matrix, then its determinant is define as
det(A) = |A| = a11A11 + a12A12 + a13A13.
18
Similarly, more general for n × n matrix, we define
as
det( A)  A   a A ,
n  2,
n
ij
ij
1
where summation is on i for any fixed value of jth
column (1 ≤ j ≤ n), or on j for any fixed value
of ith row (1 ≤ i ≤ n) and Aij is the cofactor of
element aij .
19
Theorem (The Laplace Expansion Theorem)
The determinant of an n × n matrix A = {aij}, when
n ≥ 2, can be computed as
det( A)  a A  a A  ...  a A   a A ,
which is called the cofactor expansion along the ith
row and also as
det( A)  a A  a A  ...  a A   a A ,
n
i1
i1
i2
i2
in
in
j 1
ij
ij
ij
ij
n
1j
1j
2j
2j
nj
nj
i 1
is called cofactor expansion along jth column.
It is called Laplace Expansion Theorem.
20
Note that the cofactor and minor of an element aij
differs only in sign, that is, Aij = ±Mij .
A quick way for determining whether to use the +
or − is to use the fact that the sign relating Aij
and Mij is in the ith row and jth column of the
checkerboard array
21
Definition (Cofactor Matrix)
If A is any n × n matrix and Aij is the cofactor of aij ,
then the matrix
is called the matrix of cofactor from A.
22
Definition (Adjoint of a Matrix)
If A is any n × n matrix and Aij is the cofactor of aij
of A, then the transpose of this matrix is called the
adjoint of A and is denoted by Adj(A).
23
Theorem (Properties of the Determinant)
Let A be an n × n matrix:
1. The determinant of a matrix A is zero if any row
or column is zero or equal to a linear combination
of other rows and columns.
2. A determinant of a matrix A is changed in sign if
the two rows or two columns are interchange.
24
3. The determinant of a matrix A is equal to the
determinant of its transposed
.
4. If the matrix B is obtained from the matrix A by
multiplying every element in one row or in
one column by k, then determinant of the matrix B
is equal to k times the determinant of A.
25
5. If the matrix B is obtained from the matrix A by
adding to a row (or a column) of a multiple
of another row (or another column) of A, then
determinant of the matrix B is equal to the
determinant of A.
6. If two rows or two columns of a matrix A are
identical, then the determinant is zero.
26
7. The determinant of a product of matrices is the
product of the determinants of all matrices.
8. The determinant of a triangular matrix (uppertriangular or lower-triangular matrix) is equal
to the product of all their main diagonal elements.
27
9. The determinant of an n×n matrix A times scalar
multiple k equal to kn times the determinant of the
matrix A, that is
det(kA) = kn det(A).
10. The determinant of the kth power of a matrix A
equal to the kth power of the determinant
of the matrix A, that is
det(Ak) = (det(A)) k.
11. The determinant of a scalar matrix (1 × 1) is equal to
the element itself.
28
3 2  1
A  1 6
3 
2  4 0 
A13
M 11
 ( 1)11 6 3
4 0


cof ( A)  ( 1) 2 1 24 01
 31 2  1
 ( 1) 6 3

( 1)
( 1)
( 1)
1 2 1 3
2 0
2 2 3  1
2
0
3 2 3  1
1
3

2 4 
3 2 3 2 
( 1)
2 4

3 3 3 2
( 1)

1 6

( 1)
1 3 1
6
6  16 
12
cof (A)   4
2
16 
12  10 16 
T
cof ( A)T
20
6  16 
4 12 
12
 12
  4
2
16   adj( A)   6
2  10 
12  10 16 
 16 16 16 
Theorem
If A is an invertible matrix, then
1. det(a)  0
2. det(A )  det(1A)
( A)
A
4.
3. A  Adj
(adj( A)) 
 adj( A
det( A)
det( A)
1
1
5.
29
Adj( A)
det(adj( A)) 
det( A)
1
1
)  adj( A1 )
By using this Theorem we can find the inverse of a
matrix by showing that determinant of a
matrix not equal to zero and by using adjoint and
determinant of the given matrix A.
Matrix Inversion Method
If matrix A is nonsingular, then the linear system
Ax = b,
always has a unique solution for each b,
since the inverse matrix A−1 exists, so the solution of
this system can formally expressed as
A1 Ax  A1b  Ix  A1b,
gives
x  A1b
30
If A is a square invertible matrix, there exists a
sequence of elementary row operations that carry
A to the identity matrix I of the same size, that is,
A → I.
This same sequence of row operations
carries I to A−1, that is, I → A−1.
This can be also written as
[A| I] → [I |A -1].
20
Theorem
For an n × n matrix A, the following properties are
equivalent:
1. The inverse of matrix A exists, that is, A is nonsingular.
2. The determinant of matrix A is nonzero.
3. The homogeneous system Ax = 0 has a trivial solution x = 0.
4. The nonhomogeneous system Ax = b has a unique solution.
20
Not all matrices have inverses.
Singular matrices don’t have inverse and thus the corresponding
system of equations does not have a unique solution.
The inverse of a matrix can also be computed by using the
following numerical methods for linear systems, called,
Gauss-elimination method,
Gauss-Jordan method
and LU-decomposition method
but the best and simplest method for finding the inverse of a
matrix is to perform the Gauss-Jordan method on the augmented
matrix with identity matrix of same size.
20
20