Download Direct Proportion

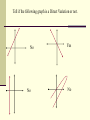
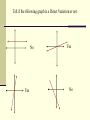
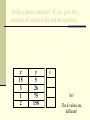
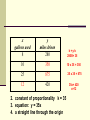
Unit 4: Direct Proportion
Update your Table of Contents:
IT / NOT IT
 Look at the IT / NOT IT examples on the next
four slides and decide what you think makes
“IT” fit each of the categories….
IT/NOT IT
Direct Proportion
also known as
Direct Variation
Consider this:
1.
On Friday chicken
biscuits are sold before
school for $2.50 each.
Complete the chart to the
right.
What number do you
think should go in the “?”
column? How do you
know?
$2.50, because every biscuit
costs $2.50.
# of
biscuits
2.
1
2
5
times =Total cost
?
Direct Proportion Defined:
The relationship between 2
quantities where one
quantity changes based on
what happens to the other
quantity.
Direct Proportion
 Look at the BISCUIT table.
 Does the cost per biscuit change? no – it is always $2.50
 What affects the total cost? the # of biscuits
 The number of biscuits determines the total
cost.
 The number of biscuits is “x” and the total
cost is “y”.
 What equation could we write to represent
the total cost of the biscuits?
y = 2.50 x
Direct Proportion: Equations
 The cost of the biscuits is the same no matter
how many you buy.
 Each time the number of biscuits changes, it
changes by the same amount….$2.50 per
biscuit. It is the constant of proportionality. (k)
y = 2.50 x
Constant of Proportionality (AKA: unit rate)

 All equations in a direct proportion are in the
form y = k x
Direct Proportion : Equations
IS a DIRECT VARIATION
NOT!
y = 3x
y = 3x +1
y=x
y = x-1
y=½x
or
y = 1000000x
y=x/2
y=x+3
y = 3/x
What is the constant of proportionality for
each of these equations?
Direct Proportion : Graphs
 Look at the graph at the bottom of your notes
 Take 5 minutes to work with your shoulder
partner to graph the biscuit table
 What do you notice about your graph?
Direct Variation and its graph
Observations:
1. the graph will always be a straight line
2. The graph will always go through…
the ORIGIN!!!!!
(0,0)
Special point known
as the “ORIGIN”
Tell if the following graph is a Direct Variation or not.
No
No
Yes
No
Tell if the following graph is a Direct Variation or not.
No
Yes
Yes
No
Direct Proportion: Tables
 Spend 5 minutes completing the Movies
Rock! Table.
 How did you know what to put for y values?
direct proportion : the table
People
(x)
Total Cost
(y)
3
$33
5
$55
9
$99
Notice…
• As x increases in value, y increases by the same factor ….
This “same factor” is the constant of proportionality.
You can find the constant of proportionality k by using k = y/x
Is it a Direct Proportion?
x
6
7
8
y
12
14
16
y
k
x
Note, x increases: 6 , 7 , 8
and y increases: 12, 14, 16
•Is it a direct proportion?
•Find the constant of proportionality for each row using k =y/x.
k = 12/6 or 2
The constant of proportionality in the table above is 2.
If all the values are the same it is a Direct Proportion
The equation would be y=2x
Is this a direct variation? If yes, give the
constant of variation (k) and the equation.
x
8
14
18
20
y
4
7
9
10
Yes!
k = 10/20 or ½
k= 9/18 or ½
k= 7/14 or ½
k= 4/8 or ½
Equation?
y = 1/2 x
Is this a direct variation? If yes, give the
constant of variation (k) and the equation.
x
15
3
1
2
y
5
26
75
150
k
No!
The k values are
different!
Direct Proportion: Word Problems
A car uses 8 gallons of gasoline to travel 280 miles. If the
gas used and miles driven are proportional, how far will the
car go on 10 gallons of gas? 25 gallons of gas? How many
gallons are needed to drive 420 miles?
1. Spend 5 minutes with your shoulder partner completing
the table from the word problem.
2. What is the constant of proportionality?
3. What equation would represent the scenario?
4. What would the graph look like?
x
gallons used
8
y
miles driven
280
10
350
25
875
12
420
2. constant of proportionality k = 35
3. equation: y = 35x
4. a straight line through the origin
k = y/x
280/8= 35
10 x 35 = 350
25 x 35 = 875
35x= 420
x=12