Download Icc5

Switching Units
Types of switching elements
 Telephone switches

switch samples
INPUTS
 Datagram routers
 switch datagrams
 ATM switches

switch ATM cells
OUTPUTS
#2
Look Inside a Router
Two key router functions:
 run routing algorithms/protocol (RIP, OSPF, BGP)
 switching datagrams from incoming to outgoing ports
#3
3
Repeaters, bridges, routers,
and gateways
 Repeaters/Hubs: at physical level (L1)
 Bridges: at datalink level (L2)
 based on MAC addresses
 discover attached stations by listening
 Routers: at network level (L3)
 participate in routing protocols
 Application level gateways: at application level (L7)
 treat entire network as a single hop
 Gain functionality at the expense of forwarding
speed

for best performance, push functionality as low as
possible
#4
Types of services
 Packet vs. circuit switches
 packets have headers and samples don’t
 Connectionless vs. connection oriented
 connection oriented switches need a call setup
 setup is handled in control plane by switch
controller
 connectionless switches deal with selfcontained datagrams
Packet
switch
Circuit
switch
Connectionless
(router)
Internet router
??
Connection-oriented
(switching system)
ATM switching system
Telephone switching
system
#5
Other switching unit functions
 Participate in routing algorithms
to build routing tables
 Next Lecture!

 Resolve contention for output trunks
 buffer scheduling
 Previous Lecture!
 Admission control
 to
guarantee resources to certain streams
#6
Requirements
 Capacity of switch is the maximum rate at which it
can move information, assuming all data paths are
simultaneously active
 Primary goal: maximize capacity

subject to cost and reliability constraints
 Circuit switch must reject call if can’t find a path
for samples from input to output

goal: minimize call blocking
 Packet switch must reject a packet if it can’t find
a buffer to store it awaiting access to output
trunk

goal: minimize packet loss
 Subgoal: Don’t reorder packets
#7
Internal switching
 In a circuit switch, path of a sample is determined
at time of connection establishment

No need for a sample header--position in frame is enough
 In a packet switch, packets carry a destination
field

Need to look up destination port on-the-fly
 Datagram
 lookup based on entire destination address
 Cell
 lookup based on VCI – used as an index to a table
 Other than that, switching units are very similar
#8
Blocking in packet switches
 Can have both internal and output blocking
 Internal
 no path to output
 Example: head of line blocking.
 Output

output link busy
 If packet is blocked, must either buffer or
drop it
#9
Dealing with blocking
 Overprovisioning

internal links much faster than inputs
 Buffers
 at input or output
 Backpressure

if switch fabric doesn’t have buffers, prevent
packet from entering until path is available
 Parallel switch fabrics
 increases effective switching capacity
#10
Three generations of packet
switches
 Different trade-offs between cost and
performance
 Represent evolution in switching capacity,
rather than in technology
 With
same technology, a later generation
switch achieves greater capacity, but at
greater cost
 All three generations are represented in
current products
#11
First generation switch
computer
CPU
queues in memory
linecard
linecard
linecard
 Most Ethernet switches and cheap packet
routers
 Bottleneck can be CPU, host-adaptor or
I/O bus, depending
#12
Second generation switch
computer
bus
front end processors
or line cards
 Port mapping intelligence in line cards
 Bottleneck is the bus (or ring)
#13
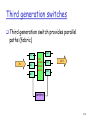
Third generation switches
 Third generation switch provides parallel
paths (fabric)
OLC
ILC
IN
ILC
NxN
packet
switch
fabric
ILC
OLC
OUT
OLC
control
#14
Third generation (contd.)
 Features
self-routing fabric
 output buffer is a point of contention

• unless we arbitrate access to fabric
 potential
for unlimited scaling,
• as long as we can resolve contention for output buffer
#15
Line Cards
(for CRS-1)
#16
CRS-1 routers
#17
Switching - Fabric
Switching: abstract model
Number of connections: from few (4 or 8) to huge (100K)
#19
Multiplexors and demultiplexors
 Multiplexor: aggregates sessions
 N input lines
 Output runs N times as fast as input
 Demultiplexor: distributes sessions
 one input line and N outputs that run N times
slower
 Can cascade multiplexors
1
2
1
2
MUX
N
1 2
N
De-Mux
N
#20
Time division switching
 Key idea: when demultiplexing, position in
frame determines output link
 Time division switching interchanges
sample position within a frame:
 Time
M
U
X
slot interchange (TSI)
TSI
D
E
M
U
X
#21
Time Slot Interchange (TSI) :
example
sessions: (1,3) (2,1) (3,4) (4,2)
1
2
3
4
4 3 2 1
1
2
3
4
2
4
3 1 4 2
1
3
Read and write to shared memory in different order
#22
TSI
 Simple to build.
 Multicast: easy (why?)
 Limit is the time taken to read and write to memory
 For 120,000 telephone circuits
 Each circuit reads and writes memory once every 125 ms.
 Number of operations per second : 120,000 x 8000 x2
 each operation takes around 0.5 ns => impossible with
current technology
 Need to look to other techniques
#23
Space division switching
 Each sample takes a
different path
through the switch,
depending on its
destination
 Crossbar: Simplest
possible space-division
switch
 Crosspoints can be
turned on or off
i
n
p
u
t
s
outputs
#24
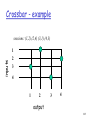
Crossbar - example
inputs
sessions: (1,2) (2,4) (3,1) (4,3)
1
2
3
4
1
2
3
4
output
#25
Crossbar
 Advantages:
 simple to implement
 simple control
 strict sense non-blocking
 Multicast
• Single source multiple destination ports
 Drawbacks
number of crosspoints, N2
 large VLSI space
 vulnerable to single faults

#26
Time-space switching
 Precede each input trunk in a crossbar with
a TSI
 Delay samples so that they arrive at the
right time for the space division switch’s
schedule
Crosspoint: 4 (not 16)
1
2
3
4
M
U
X
M
U
X
memory speed : x2 (not x4)
2 1
TSI
12
4 3
TSI
43
DeMux
DeMux
#27
Finding the schedule
 Build a routing graph
 nodes - input links
 session connects an input and output nodes.
 Feasible schedule
 Computing a schedule
 compute perfect matching.
1
2
1
2
3
4
3
4
#28
Time-Space: Example
time 1
time 2
2 1
2 1
4 3
TSI
3 4
3
1
2
4
TSI
Internal speed = double link speed
#29
Internal Non-Blocking Types
 Re-arrangeable
 Can route any permutation from inputs to outputs.
 Strict sense non-blocking
 Given any current connections through the switch.
 Any unused input can be routed to any unused output.
 Wide sense non-blocking.
 There exists a specific routing algorithm, s.t.,
 for any sequence of connections and releases,
 Any unused input can be routed to any unused output,
 assuming all the sequence was served by the routing
algorithm.
#31
Circuit switching - Space division
 graph representation
 transmitter nodes
 receiver nodes
 internal nodes
 Feasible schedule
 edge disjoint paths.
 cost function
 number of crosspoints (complexity of AxB is
AB)
 internal nodes
#32
Crossbar - example
1
2
3
4
1
2
3
4
#33
outputs
inputs
Another Example
#34
Another Example
outputs
inputs
sessions: (1,3) (2,6) (3,1) (4,4) (5,2) (6,5)
#35
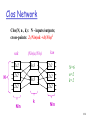
Clos Network
Clos(N, n , k) : N - inputs/outputs;
cross-points: 2 (N/n)nk + k(N/n)2
nxk
2x2
N
2x2
(N/n)x(N/n)
3x3
3x3
2x2
N/n
kxn
2x2
2x2
N=6
n=2
k=2
2x2
k
N/n
#36
Clos Network - strict sense
non-blocking
 Holds for k  2n-1
 Proof Methodology:





Recall: IF [A,B  S and |A|+|B| > |S|] then A∩ B≠Ø
S= The k middle switches
A = middle switches reachable from the inputs
B = middle switches reachable from the outputs
Our case:
• |S|=k
• |A| ≥ k-(n-1)
• |B| ≥ k-(n-1)
#37
Clos Network - strict sense
non-blocking
 Holds for k  2n-1
 Proof:




Consider an idle input and output
Input box connected to at most n-1 middle layer switches
output box connected to at most n-1 middle layer
switches
There exists an ”unused" middle switch good for both.
n-1
nxk
kxn
n-1
#38
Example
Clos(8,2,3)
Need to route a new call
2x3
4x4
3x2
2x3
4x4
3x2
2x3
2x3
4x4
3x2
N=8
n=2
k=3
3x2
#39
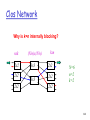
Clos Network
Why is k=n internally blocking?
nxk
2x2
2x2
2x2
(N/n)x(N/n)
3x3
3x3
kxn
2x2
2x2
N=6
n=2
k=2
2x2
#40
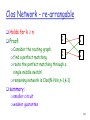
Clos Network - re-arrangable
 Holds for k  n
1
2
 Proof:
 Consider the routing graph.
3
4
 find a perfect matching.
 route the perfect matching through a
single middle switch!
 remaining network is Clos(N-N/n,n-1,k-1)
1
2
3
4
 summary:
 smaller circuit
 weaker guarantee
#41
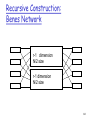
Recursive Construction: basis
The basic element:
The dimension: r=0
The two states:
#42
Recursive Construction:
Benes Network
r-1 dimension
N/2 size
r-1 dimension
N/2 size
#43
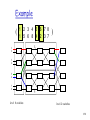
Example 16x16
#44
Benes Networks
 Symmetry
 Size:
 F(N) = 2(N/2)*4 + 2F(N/2) = O(N log N)
 Rearrangable

Clos network with k=2 n=2
 Proof I:
 Build routing graph.
 Find 2 matchings
 route one in the upper Benes and the other in
the lower.
#45
Greedy permutation routing
 Start with an arbitrary node i1

set i1 to upper.
 At the output, o1 , a new constraint,
 set o2 to lower.
 Continue until no new constraint.

Completing a cycle.
 Continue until done.
 Solve for the upper and lower Benes
recursively.
#46
Example: Benes Network for r=2
I1
1
2
3
4
5
6
7
8
level 0 switches
I2
level 2r switches
#47
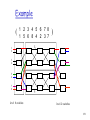
Example
(
1 2 3 4 5 6 7 8
1 5 6 8 4 2 3 7
1
2
)
I1
3
4
5
6
7
8
level 0 switches
I2
level 2r switches
#48
Example
(
1 2 3 4 5 6 7 8
1 5 6 8 4 2 3 7
1
2
)
I1
3
4
5
6
7
8
level 0 switches
I2
level 2r switches
#49
Example
(
1 2 3 4 5 6 7 8
1 5 6 8 4 2 3 7
1
2
)
I1
3
4
5
6
7
8
level 0 switches
I2
level 2r switches
#50
Example
(
1 2 3 4 5 6 7 8
1 5 6 8 4 2 3 7
1
2
)
I1
3
4
5
6
7
8
level 0 switches
I2
level 2r switches
#51
CRS-1 Switch Fabric Overview
50 Gbps
136 Bytes cells
40 Gbps
8 of 8
8
S1
1
16
S2
S3
2 of 8
2
Line Card
100 Gbps/LC(2)
(2.5X Speedup)
Fabric
Chassis
2
1 of 8
S1
S2
S3
1
Line Card
2 LEVELS OF PRIORITY
MULTICAST SUPPORT
HP Low latency traffic
1M multicast groups
LP Best effort traffic
S1
S2
S3
1296 x 1296 buffered non-blocking switch
Multi-stage Interconnect—3 Stage Benes topology
#52
Basic Router Architecture
3 Main components: Line cards,Switching mechanism,
Route Processor(s), Routing Applications
Forwarding Component
Control Components
Interconnect
#53
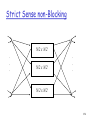
Strict Sense non-Blocking
N/2 x N/2
.
.
.
N/2 x N/2
.
.
.
N/2 x N/2
#54
Properties
 Size:
 F(N) = 2N*6 + 3F(N/2) = O( N1.58 )
 strict sense non-blocking
 Clos network with k=3 n=2
 Better parameters:
 n=sqrt{N}, k=2sqrt{N}-1
 recursive size sqrt{N} x sqrt{N}
 Circuit size O(N log2.58 N)
#55
Cantor Networks
 m copies of Benes network.
 For m = log N its strict sense non-blocking
 Network size N log2 N
 Example
#56
Cantor Network
m=4
#57
Proof
Sketch:
 Benes network:
• 2 log N -1 layers,
• N/2 nodes in layer.
• Middle layer= layer log N -1
 Consider the middle layer of the Benes Networks.
 There are Nm/2 nodes in in all of them combined.
 Bound (from below) the number of nodes
reachable from an input and output.
 If the sum is more than Nm/2:


There is an intersection
there has to be a route.
#58
Proof Sketch:
 Let A(k) = number of nodes reachable at
level k.
 A(0)=m
 A(1)= 2A(0)-1
 A(2)=2A(1)-2
 A(k)=2A(k-1) - 2k-1 = 2k A(0) - k 2k-1
 A(log N -1) = Nm/2 - (log N -1) N/4
 Need that: 2A(log N -1) > Nm/2.

2[Nm/2 - (log N -1) N/4] > Nm/2.
 Hold for m> log N-1.
#59
Advanced constructions
 There are networks of size O(N log N).
 the constants are huge!
 Basic paradigm also applies to large packet
switches.
#60