Download 離散對數密碼系統 - 國立交通大學資訊工程學系NCTU Department of

離散對數密碼系統
交通大學資訊工程系
陳榮傑
1
Outline
• 離散對數問題 (Discrete Logarithm Problem)
• 離散對數演算法 (DL Algorithms)
–
–
–
–
–
A trivial algorithm
Shanks’ algorithm
Pollard’s algorithm
Pohlig-Hellman algorithm
Adleman’s algorithm (the index calculus method)
• 離散對數密碼系統 (Cryptosystems based on DL)
– Key distribution
– Encryption
– Digital signature
2
Discrete Logarithm Problem
• Let G is a finite cyclic group of size n generated by
generator g, i.e.
G = <g> = {g i | i = 1, 2, …, n}
or {g i | i = 0, 1, …, n-1}
– Given g and i, it is easy to compute gi by repeated squaring
– Discrete logarithm problem
x
Given a  G , find x such that g  a
We denote x  log g a (or ind g a )
3
Discrete Logarithm Problem
• Example 1
G = Z*19 = { 1, 2, …, 18}
n=18, generator g = 2
i
1
2
3
4
5
6
7
8
9
gi
2
4
8
16
13
7
14
9
18
10
11
12
13
14
15
16
17
18
17
15
11
3
6
12
5
10
1
then log214 = 7
log26 = 14
4
Discrete Logarithm Problem
• Example 2
G=GF*(23) with irreducible poly. p(x) = x3 + x +1
G=Z*p/p(x) = { 1, x, x2, 1+x, 1+x2, x+x2, 1+x+x2 }
n=7, generator g = x
i
gi
1
x
2
x2
3
x 1
4
5
x2  x
x2  x  1
6
x2  1
7
1
then logx(x+1) = 3
logx(x2+x+1) = 5
logx(x2+1) = 6
5
離散對數演算法 (DL Algorithms)
•
•
•
•
•
A trivial algorithm
Shanks’ algorithm
Pollard rho discrete log algorithm
Pohlig-Hellman algorithm
The index calculus method
6
Algorithms for Discrete Logarithm
• Discrete Logarithm Problem in Z*p
given generator g and a in Z*p,
find x in Zp-1 such that a = gx mod p
• A trivial algorithm
– Compute gi for all i
– Search table for a
– Time complexity O(p)
7
Algorithms for Discrete Logarithm
• Shanks’ algorithm (1972)
– Compute L1 = {(i, gmi), i = 0, 1, …, m-1}
L2 = {(i, ag-i), i = 0, 1, …, m-1}
– where m = ceiling((p-1) ½)
Sort L1 and L2 with respect to the 2nd coordinate.
– Find the same 2nd coordinate from L1 and L2, say,
(q, gmq), (r, ag-r), to get gmq =ag-r.
So a = gmq + r and x=mq+r.
– Time complexity O(mlogm) = O(p 1/2 logp)
– Space complexity O(p 1/2)
8
Algorithms for Discrete Logarithm
Example
log215 mod 19 =?
G = Z*19 = { 1, 2, …, 18}
g = 2, g-1 = 10, n=p-1 = 18, m = 5, gm = 13
a = 15
L1: (i, gmi)
(0, 1)
(1, 13)
(2, 17)
(3, 12)
(4, 4)
L2: (i, ag-i)
(0, 15)
(1, 17)
q=2
(2, 18)
r=1
(3, 9)
mq + r = 11
(4, 14)
log215 mod 19 = 11
9
Algorithms for Discrete Logarithm
• Pollard rho discrete logarithm algorithm (1978)
compute integers s and t such that a s  g t
– partition the group G into three roughly equal-sized set
S1 , S2 and S3 . Let x0=1G and x0 is not in S2
xi1 
axi
for xi  S1
2
for xi  S2
gxi
for xi  S3
xi
Let xi  a ai g bi
10
Algorithms for Discrete Logarithm
ai  1(mod n)
2ai (mod n)
ai
for xi  S1
for xi  S 2
for xi  S3
bi
bi 1  2bi (mod n)
bi  1(mod n)
for xi  S1
for xi  S 2
for xi  S3
ai1 
where n = p-1 when G = Z*p
11
Algorithms for Discrete Logarithm
•
1
We should expect some integer i  3n 2 such that
xi  x2i , then this gives a s  g t
t  b2i  bi (mod n)
with s  ai  a2i (mod n)
If gcd( s, n)  1,
then compute u such that us  1(mod n)
ut
a

g
and we have
, so that log g a  ut (mod n).
If gcd( s, n)  d  1,
little work to do... (Omitted)
12
Algorithms for Discrete Logarithm
• Pohlig-Hellman algorithm (1978)
(DLP: find m s.t. αm = c mod q)
Suitable for q-1 containing only small prime divisors
Assume m is the discrete logarithm of c (i.e. c = αm )
• Base case : If q-1 = 2n and m  m0  m1 2    mn 1 2 n 1
because αq-1 = 1
hence
c
q 1
2
 ( )
m
c 
c1
q 1
4
q 1
2
 m0
 (
 (
m0  m1 2 mn 1 2n 1
)
q 1
2
 c1
m1  m2 2  mn 1 2n  2
….
So we can compute m
)
q 1
2

m1
q 1
2

m0
q 1
2

1 if m0  0,
 1 if m0  1
1 if m1  0,
  1 if m1  1
13
Algorithms for Discrete Logarithm
• General case :
q  1  p1n1 p2n2 ... pknk
Let m(i) = m (mod pini)
then apply the Chinese Remainder Theorem,
we can compute m.
How to compute m(i) ? (similar to the base case, see next page)
14
Algorithms for Discrete Logarithm
Let m (1)  m0  m1 p1    mn 1 p1n 1
1
1
1  
then c
q1
p1
q 1
p1
q 1
m p1
 ( )
 (
m
(1)
)
q 1
p1

m0
q 1
p1
 1
m0
c    m0  c1
q 1
c1 p12  1
m1
…..
So we can compute m(i) and then apply CRT to get m
– Time complexity: O((log2q)2) + factoring q-1
15
Algorithms for Discrete Logarithm
• The index calculus method (Suitable only for G=Zp*)
(1st step)
To find the discrete logarithms of the B primes in the factor base.
  {p 1 , p 2 , ..., p B }.
(2nd step)
To compute the discrete logarithm of a desired element a,
using the knowledge of the discrete logarithms of the elements
in the factor base.
16
Algorithms for Discrete Logarithm
• Example
log59451 mod 10007=?
Choose B={2, 3, 5, 7}. Of course log55=1.
Use = 9865 mod 10006
lucky exponents 4063, 5136, and 9865
54063 mod 10007 = 42 = 2 * 3 * 7
55136 mod 10007 = 54 = 2 * 33
59865 mod 10007 = 189 = 33 * 7
And we have three congruences:
log52 + log53 + log57 = 4063 mod 10006
log52 + 3 log53 = 5136 mod 10006
3 log53 + log57 = 9865 mod 10006
17
Algorithms for Discrete Logarithm
There happens to be a unique solution modulo 10006
log52=6578, log53=6190, and log57=1301
Choose random exponent s = 7736 and try to calculate
ags = 9451*57736 mod 10007 = 8400
Since 8400 = 24*3*52*7 factors over B, we obtain
log59451 = (4 log52 + log53 + 2 log55 + log57 – s) mod 10006
= (4*6578 + 6190 + 2*1 +1301 – 7736) mod 10006
= 6057 mod 10006
18
離散對數密碼系統
(Cryptosystems based on DL)
• Key Distribution
– Diffie-Hellman, 1976
• Encryption
– Massey-Omura cryptosystem, 1983
• Digital Signature
– ElGamal, 1985
– DSA(Digital Signature Algorithm), 1992
19
Diffie-Hellman Key Exchange Algorithm
• Global Public Elements
– q : prime number
– α: α< q and α is a primitive root of q
• User A Key Generation
– Select private XA : XA< q
– Calculate public YA : YA= αXA mod q
• User B Key Generation
– Select private XB : XB< q
– Calculate public YB : YB= αXB mod q
• Generation of Secret Key by User A
– K = (YB)XA mod q
• Generation of Secret Key by User B
– K = (YA)XB mod q
20
User A
Generate
random XA < q ;
Calculate
YA = αXA mod q
User B
YA
YB
Calculate
K = (YB)XA mod q
Generate
random XB < q ;
Calculate
YB = αXB mod q
Calculate
K = (YA)XB mod q
Diffie-Hellman Key Exchange
21
Massey-Omura for message transmission
• Parameters
– q : prime number
– e : a random private integer
• 0 < e < q and gcd ( e, q-1) = 1
– d : an inverse of e
• d = e-1 mod q-1 , i.e., de≡1 mod q-1
– M : a message to be encrypted and decrypted
• User A wants to send a message M to User B
– User A : eA and dA are both private
– User B : eB and dB are both private
22
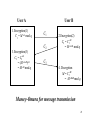
User A
1.Encryption(1)
C1 = M eA mod q
User B
C1
C2
3.Encryption(3)
C3 = C2dA
= (M eAeB)dA
= M eB mod q
2.Encryption(2)
C2 = C1eB
= M eAeB mod q
C3
4. Decryption
M = C3dB
= M eBdB mod q
Massey-Omura for message transmission
23
ElGamal encryption scheme
• Parameters
–
–
–
–
–
–
–
p : a large prime
α: a primitive number in GF(p)
a : a private key, a  [1, p-1]
β : a public key , β = αa (mod p)
m : a message to be signed , m  [1, p-1]
k : a random integer that is privately selected, k  [0, p-2]
K = (p, α, a, β) : public key + private key
• Encryption
eK(m, k)=(y1, y2)
where y1 = αk mod p and y2=mβk mod p
• Decryption
m = dK(y1, y2) = y2(y1a)-1 mod p
24
ElGamal signature scheme
• 1985 ElGamal
• Parameters
–
–
–
–
–
–
p : a large prime
α: a primitive number in GF(p)
x : a private key, x [1, p-1]
y : a public key , y = αx (mod p)
m : a message to be signed , m [1, p-1]
k : a random integer that is privately selected, k  [0, p-2]
• Signature
– r = αk mod p
– m = ks + rx mod φ(p) ,where GCD( k, φ(p) ) = 1
– ( m , (r,s) ) is sent to the verifier
• Verification
– αm = rs yr mod p
– The signature (r,s) is accepted when the equality holds true.
25
Digital Signature Algorithm (DSA)
• 1992 NIST
• Parameters
–
–
–
–
–
–
p : a large prime, 512 bits
q : a large prime, 160 bits , q | p-1
g : g = h p-1/q mod q , with h  [1, p-1]
h : a one-way hash function
x : a private key, 0 < x < q
y : a public key , y = gx (mod p)
– m : a message to be signed , 0 < m < p
– k : a random integer that is privately selected, 0 < k < q
26
Digital Signature Algorithm (DSA)
• Signature
– r = (gk mod p) mod q
– s = k -1( h(m)+ rx) mod q ,where k-1 k = 1 mod q
– ( m , (r,s) ) is sent to the verifier
• Verification
–
–
–
–
check whether (r,s) [0,q] ; if not , (r,s) is not the signature
t = s -1 mod q
r’ = ( g h(m)t yrt mod p ) mod q
if r’ = r ,then (r,s) is the legal signature of message m
• Proof
g h(m)t yrt = (( g h(m)t yr )t mod p ) mod q
= (( g h(m)t (gx)r )t mod p ) mod q
= (( g h(m)+xr )t mod p ) mod q
= (( g h(m)+xr )s-1 mod p ) mod q
= ( gk mod q ) mod q
= r
27