Download EM Energy

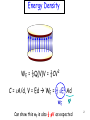
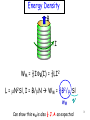
Energy Density
Work done to bring the charge in: qV
But V itself is changing as you assemble unit, ie, V=V(q)
Starts off at zero, ends at V, average V/2
So net energy stored per unit volume ½ rV
Another way to think of ½
Only 1 member of each pair
works against the other
WE = ½ SiSj qiqj/4pe0Rij
So
wE = ½ rV
W: total energy
w: energy density
1
Energy Density
WE = ½Q(V)V = ½CV2
C = eA/d, V = Ed  WE = ½ eE2 Ad
wE V
Can show this wE is also ½ rV as expected
2
Energy Density
B
I
WM = ½IFB(I) = ½LI2
L = mN2Sl, I = B/mN  WM = ½B2/m Sl
wM V
Can show this wM is also ½ J.A as expected
3
Energy Density
So electric energy is WE = ½QV, which gives energy density wE = ½rV
Capital
Letter for
Total energy
Small
Letter for
Energy density
Equivalently, we have WE = ½CV2, which gives energy density wE = ½E.D
(check for parallel plate capacitor, C = e.A/d and V = Ed)
Magnetic energy is WB = ½IF, which gives energy density wB = ½J.A
(recall I/S = J, S:area. Also, flux F = ∫B.dS = ∫(x A).dS = ∫A.dl)
Equivalently, we have WB = ½LI2, which gives energy density wB = ½B.H
Energy Density
Is energy stored in charges or fields?
Both viewpoints correct – just matter of bookkeeping
Where energy ‘sits’ is debatable, but total energy same
Integrate where
charge r sits
W = ∫½ rV dv’
OR Integrate where
field E sits
W = ∫½ eE2 dv’
5
Energy Density
Area S
B
WM = ½B2/m Sl
I
Here we have the field point of view
ie, energy density B2/2m sitting in field
lying inside solenoid occupying a volume Sl
Let’s now use the charge/current point of view
Energy density ½ J.A stored in volume
of wires around solenoid
6
Energy Density
B
WM = ½B2/m Sl
I
S0
J = (I/S0) f
Total wire volume V = Nl . 2pR . S0
#turns Length/turn
Cross sectional
area/turn
7
Energy Density
J = (I/S0) f
Total wire volume
V = Nl . 2pR . S0
B
I
WM = ½B2/m Sl
B = mNIz
A = mNIr/2 f (Check B =  x A)
Set r = R because only those terms multiply with J
WM = ½ J.AV
= ½(I/S0).(mNIR/2).(Nl.2pR.S0) rewrite I in terms of B
8
= (B2/2m) x (pR2l)
Revelation!
Although different volumes to integrate over,
result same in the end!
9
EM Energy Density
H = E/Z0
Can show then that
wE = w M
H is characterized by m
E is characterized by e
Z0= m/e
10
EM Energy Density
H = E/Z0
Can show then that
wE = w M
This makes sense! Comparison of E and H strengths is meaningless
since they have different units and dimensions.
But when comparing energy densities
both fields contribute equally to an EM signal, as expected !
11
Power flow
Along propagation direction
Charge current
J = vr
Energy current
S = v(wE + wM) = b.(1/√me)(eE2)
= bE2/Z0 = bEH = E x H
12
Power flow
= EH<cos(wt)cos(wt+f)>
= EHcos(f)/2
S = E x H : Poynting Vector (1885)
Sav = ½ Re(E x H*)
Pin = ∫S.dA
13
Energy Conservation
From Maxwell’s equations can prove
(Try it!)
-.S = J.E +
Incoming Power density
w/t
Power
Dissipation
Increasing EM
Energy Density
w = eE2/2 + B2/2m
Shows energy conservation just like
eqn of continuity gives charge conservation
-.J = r/t
14
Loss: finite conductivity
(r=0,J=sE)
Power dissipation/Vol
J=sE
I=JA
V=El
I=(sA/l)V (Ohm’s Law)
J.E = J2/s
= I2R/lA
V
Joule’s Law
R=l/sA
15