* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Direct Variation (5-3)
Two-body Dirac equations wikipedia , lookup
Debye–Hückel equation wikipedia , lookup
Equations of motion wikipedia , lookup
Bernoulli's principle wikipedia , lookup
Euler equations (fluid dynamics) wikipedia , lookup
Schrödinger equation wikipedia , lookup
Exact solutions in general relativity wikipedia , lookup
Differential equation wikipedia , lookup
Dirac equation wikipedia , lookup
Partial differential equation wikipedia , lookup
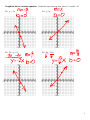
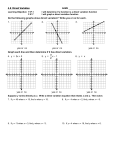
Model Direct Variation (4.6) Definition: Direct Variation is a linear function that can be written in the form y = kx (where x ≠ 0) Definition: k is called the constant of variation **Think of the y = mx + b form. ** y = kx means that m = ______ and b = ______ So all direct variations will go through the _______________________ Is the equation a direct variation? If it is, find the constant of variation (k). ** To determine if an equation is a direct variation, solve the equation for y. Ex. y = 3x Ex. y = -2x + 1 Ex. 5x + 2y = 0 Ex. 4y = 3x + 12 1 Graph the direct variation equation. (Graph like slope-intercept form, where k = m and b = 0) Ex. y = -3x Ex. y = x Ex. 2x + y = 0 Ex. 6y = 10x 2 Solve y = kx, for k To Write a Direct Variation Given one value for x and y Step 1—Find k (Use the equation above) Step 2—Write the equation y = kx and substitute your k value Given that y varies directly with x, use the specified values to write a direct variation equation that relates x and y Ex. x = 2, y = -8 Ex. x = 40, y = 15 The graph of a direct variation equation is shown. Write the direct variation of the equation. Then find the value of y, when x = 10 Ex Find k (Use the point given) • (3,4) Write the equation ______________ Use the equation to find y (substitute in x = 10) 3 Ex. The size of a file (s) varies directly with the amount of time (t) download a file. It takes 15 seconds to download a 420kb file. a) Write a direct variation that relates s and t b) How much time will it take to download a file that is 1260kb? To determine if a chart is a direct variation, find k for each pair. If k is the same for each pair, then the chart is a direct variation. If k is not the same, then it is not a direct variation. Tell whether the table represents direct variation. If so, write the direct variation equation Ex. x y 0.5 9 3 -2 1 54 -36 18 Ex. x y 8 7 2 -4 28 7 -0.5 -112 4