Mathematics with a Scientific Calculator Casio fx
... correlation; the regression line should be a good predictor. However, a negative value of r indicates that the regression line has a negative slope. A negative linear relationship exists, the points fall approximately in a descending straight line from left to right. As the x values are increasing t ...
... correlation; the regression line should be a good predictor. However, a negative value of r indicates that the regression line has a negative slope. A negative linear relationship exists, the points fall approximately in a descending straight line from left to right. As the x values are increasing t ...
Hand-book on STATISTICAL DISTRIBUTIONS for
... 3.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 3.2 Relation to Other Distributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 4 Beta distribution 4.1 Introduction . . . . . . . . . . . . . 4.2 Derivation of the Beta Distribution ...
... 3.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 3.2 Relation to Other Distributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 4 Beta distribution 4.1 Introduction . . . . . . . . . . . . . 4.2 Derivation of the Beta Distribution ...
12 6 1 6 36 12 Number of ways to get a total of after rolling two sided
... Outcomes not face card success or face card failure Finite population N 13 || number of success in population M 10 Fixed sample size n 3 || number of success in sample x 3 ...
... Outcomes not face card success or face card failure Finite population N 13 || number of success in population M 10 Fixed sample size n 3 || number of success in sample x 3 ...
Bernoulli trial
... · consider a box of 12 lighbulbs - if the chance that any one bulb is broken is 0.01 · 89% of the time there will be no broken bulbs, P(n=12,k=0,p=0.01) · 99.4% of the time there will be no more than one broken bulb, P(12,0,0.01)+P(12,1,0.01) · 99.98% of the time there will be no more than two broke ...
... · consider a box of 12 lighbulbs - if the chance that any one bulb is broken is 0.01 · 89% of the time there will be no broken bulbs, P(n=12,k=0,p=0.01) · 99.4% of the time there will be no more than one broken bulb, P(12,0,0.01)+P(12,1,0.01) · 99.98% of the time there will be no more than two broke ...
www.crm.umontreal.ca
... vertex v in G, we need to put two pebbles on any neighbor of v. We can choose the target neighbor If S is a set of distributions on G, ρ(G, S) is the number of pebbles needed to reach some distribution in S Idea: Develop an induction argument to prove Graham's conjecture ...
... vertex v in G, we need to put two pebbles on any neighbor of v. We can choose the target neighbor If S is a set of distributions on G, ρ(G, S) is the number of pebbles needed to reach some distribution in S Idea: Develop an induction argument to prove Graham's conjecture ...
Generating Random Variables from the Inverse Gaussian and First
... we can, in theory, simulate it by summing independent normal random ...
... we can, in theory, simulate it by summing independent normal random ...
Uncertainty modeling of LOCA frequencies and break size resolution
... • The LOCA table provides four distributional characteristics (rows in the table) for each break size category: mean, median, 5th and 95th percentiles. We would like to sample from distributions that match these values. • NUREG-1829 used two split p Lognormal g distributions. • NUREG/CR 6828 used Ga ...
... • The LOCA table provides four distributional characteristics (rows in the table) for each break size category: mean, median, 5th and 95th percentiles. We would like to sample from distributions that match these values. • NUREG-1829 used two split p Lognormal g distributions. • NUREG/CR 6828 used Ga ...
Chapter 13. Binomial Distributions
... Example S.13.1. Binomial Stooges. A TV station airs 10 (not necessarily different) stooge films per week. The films are chosen at random from the collection of 190 films. Since there are 97 films with Curly as the third stooge, the probability of a Curly film being chosen at random is p = 97/190. Th ...
... Example S.13.1. Binomial Stooges. A TV station airs 10 (not necessarily different) stooge films per week. The films are chosen at random from the collection of 190 films. Since there are 97 films with Curly as the third stooge, the probability of a Curly film being chosen at random is p = 97/190. Th ...
Inferences About Process Quality
... Generating Random Values from an Lognormal Distribution LN(m, s) with Excel First generate n random variables, r1, r2, …, rn, from N(0, 1). Select “Normal” under the “Distribution” menu. Type in “1” for number of variables and 10 for number of random numbers. Enter 0 for the mean and 1 for standard ...
... Generating Random Values from an Lognormal Distribution LN(m, s) with Excel First generate n random variables, r1, r2, …, rn, from N(0, 1). Select “Normal” under the “Distribution” menu. Type in “1” for number of variables and 10 for number of random numbers. Enter 0 for the mean and 1 for standard ...
PowerPoint 프레젠테이션
... CGC Shattering: pros: 1) can get soft partons 2) Good at RHIC cons: 1) no quarks and antiquarks 2) seems to produce too many JETS ...
... CGC Shattering: pros: 1) can get soft partons 2) Good at RHIC cons: 1) no quarks and antiquarks 2) seems to produce too many JETS ...
Sampling Distribution
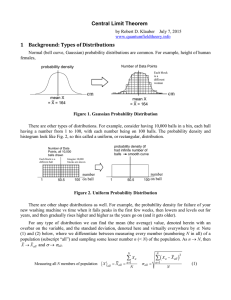
... The next three figures are the density curves of the sample means of size _, __, and __ observations from this population. As the sample size n _________, the shape of the distributions becomes ___________. The mean μ = 1, and the standard deviation decreases taking the values 1 n . The density cur ...
... The next three figures are the density curves of the sample means of size _, __, and __ observations from this population. As the sample size n _________, the shape of the distributions becomes ___________. The mean μ = 1, and the standard deviation decreases taking the values 1 n . The density cur ...
Chapter 3 Some Univariate Distributions
... We now offer a catalog of some of the more commonly encountered probability distributions (density functions). When we first look at data, in what is sometimes called ‘‘exploratory data analysis,’’ we often want to find a pdf that can act as a probability model for those data. If we can use one of t ...
... We now offer a catalog of some of the more commonly encountered probability distributions (density functions). When we first look at data, in what is sometimes called ‘‘exploratory data analysis,’’ we often want to find a pdf that can act as a probability model for those data. If we can use one of t ...
Test Code : QR ( Short answer type ) 2005
... revised value of F-ratio and draw your conclusions. 7. If X1, X2, X3 constitute a random sample from a Bernoulli population with mean p, show why [X1 + 2X2 + 3X3 ] / 6 is not a sufficient statistic for p. ...
... revised value of F-ratio and draw your conclusions. 7. If X1, X2, X3 constitute a random sample from a Bernoulli population with mean p, show why [X1 + 2X2 + 3X3 ] / 6 is not a sufficient statistic for p. ...
A numerical characteristic of extreme values
... Rapidly varying tail distributions are various. · Very rapid tail decay : the normal distribution and the Rayleigh distribution. · Middle tail decay: the exponential type, i.e. the exponential distribution, the Gamma distribution, the Chi-square distribution, the generalized inverse Gaussian distri ...
... Rapidly varying tail distributions are various. · Very rapid tail decay : the normal distribution and the Rayleigh distribution. · Middle tail decay: the exponential type, i.e. the exponential distribution, the Gamma distribution, the Chi-square distribution, the generalized inverse Gaussian distri ...
A Monte-Carlo Calculation of Pi
... The only processes that are truly random are those that occur in nature. A naturally occurring process that has an element of randomness in it is often referred to as a stochastic process. In order to model such phenomena it is necessary to generate numbers that are good approximations to truly rand ...
... The only processes that are truly random are those that occur in nature. A naturally occurring process that has an element of randomness in it is often referred to as a stochastic process. In order to model such phenomena it is necessary to generate numbers that are good approximations to truly rand ...
Algorithms for Distributions
... (with replacement) one element from a setPof K elements. For example a random variable X having the n B(n, p) distribution can be written as X = i=1 Yi where each of the Y ’s is either one (with probability p) or zero (with probability 1 − p). A multinomial random vector (X1 , . . . , Xk ) with n tr ...
... (with replacement) one element from a setPof K elements. For example a random variable X having the n B(n, p) distribution can be written as X = i=1 Yi where each of the Y ’s is either one (with probability p) or zero (with probability 1 − p). A multinomial random vector (X1 , . . . , Xk ) with n tr ...
Random-Number and Random
... • Step 1. Set n = 0, and P = 1 • Step 2. Generate a random number Rn+1 and let P = P. Rn+1 • Step 3. If P < e-, then accept N = n. Otherwise, reject current n, increase n by one, and return to step 2 • How many random numbers will be used on the average to generate one Poisson variate? ...
... • Step 1. Set n = 0, and P = 1 • Step 2. Generate a random number Rn+1 and let P = P. Rn+1 • Step 3. If P < e-, then accept N = n. Otherwise, reject current n, increase n by one, and return to step 2 • How many random numbers will be used on the average to generate one Poisson variate? ...
MA 1125 Lecture 12 - Mean and Standard Deviation for the Binomial
... This is a theoretical computation that applies to all conceivable repetitions of the experiment, so we’re doing a computation on a population. That means that we’re computing the parameter µ (the population mean). This is really a short cut to listing out one billion 0’s, three billion 1’s, three bi ...
... This is a theoretical computation that applies to all conceivable repetitions of the experiment, so we’re doing a computation on a population. That means that we’re computing the parameter µ (the population mean). This is really a short cut to listing out one billion 0’s, three billion 1’s, three bi ...
The Central Limit Theorem - Student Friendly Quantum Field Theory
... Bottom line: For the classical central limit theorem, measurements must be independent of one another. 2.3.2 Randomness of measurements For the central limit theorem, measured variable (like number on a ball Xi above) must vary randomly with measurements. By way of example, if balls in the above exa ...
... Bottom line: For the classical central limit theorem, measurements must be independent of one another. 2.3.2 Randomness of measurements For the central limit theorem, measured variable (like number on a ball Xi above) must vary randomly with measurements. By way of example, if balls in the above exa ...
Mean - gwilympryce.co.uk
... • Areas under the standard normal curve between different z-scores are equal to areas between corresponding values on any normal distribution • Tables of areas have been calculated for each z-score, – so if you standardise your observation, you can find out the area above or below ...
... • Areas under the standard normal curve between different z-scores are equal to areas between corresponding values on any normal distribution • Tables of areas have been calculated for each z-score, – so if you standardise your observation, you can find out the area above or below ...
Chapter Two: Describing Distributions with Numbers Besides the
... Where a density curve comes from? Usually it comes from the limit of a sequence of ...
... Where a density curve comes from? Usually it comes from the limit of a sequence of ...
INSTITUTE OF ACTUARIES OF INDIA EXAMINATIONS 22
... Q 6) Each year an insurer issues a number of household insurance policies. The premium for each of these policies is Rs 125. The number of claims from each policy has a Poisson distribution with parameters 0.2 and individual claim amounts have a Lognormal distribution with parameters µ = 5 and σ2 = ...
... Q 6) Each year an insurer issues a number of household insurance policies. The premium for each of these policies is Rs 125. The number of claims from each policy has a Poisson distribution with parameters 0.2 and individual claim amounts have a Lognormal distribution with parameters µ = 5 and σ2 = ...
Transforming data lecture notes
... Any given number can be expressed as y to the x power in an infinite number of ways. For example, if we were talking about base 10, 1 is 100, 100 is 102, 16 is 101.2, and so on. Thus, log10(100)=2 and log10(16)=1.2. However, base 10 is not the only option for log transformations. Another common opti ...
... Any given number can be expressed as y to the x power in an infinite number of ways. For example, if we were talking about base 10, 1 is 100, 100 is 102, 16 is 101.2, and so on. Thus, log10(100)=2 and log10(16)=1.2. However, base 10 is not the only option for log transformations. Another common opti ...
Multimodal distribution

In statistics, a bimodal distribution is a continuous probability distribution with two different modes. These appear as distinct peaks (local maxima) in the probability density function, as shown in Figure 1.More generally, a multimodal distribution is a continuous probability distribution with two or more modes, as illustrated in Figure 3.