Problem of the Week - Sino Canada School
... Divisibility by 2: A number is divisible by 2 if the last digit is even. Divisibility by 3: A number is divisible by 3 if the sum of the digits is divisible by 3. For example, 1295 is not divisible by 3 since 1 + 2 + 9 + 5 = 17 which is not divisible by 3. However, 1296 is divisible by 3 since 1 + 2 ...
... Divisibility by 2: A number is divisible by 2 if the last digit is even. Divisibility by 3: A number is divisible by 3 if the sum of the digits is divisible by 3. For example, 1295 is not divisible by 3 since 1 + 2 + 9 + 5 = 17 which is not divisible by 3. However, 1296 is divisible by 3 since 1 + 2 ...
Problem:
... determining if a large number is prime or composite. Every number has one and itself as a factor. Thus, if we could find one factor of 621, other than 1 and itself, we could prove that 621 is composite. One way to find factors of large numbers quickly is to use tests for divisibility. ...
... determining if a large number is prime or composite. Every number has one and itself as a factor. Thus, if we could find one factor of 621, other than 1 and itself, we could prove that 621 is composite. One way to find factors of large numbers quickly is to use tests for divisibility. ...
alternatives to zermelo`s assumption
... Theorem 1. The class of all well-ordered rearrangements of the positive integers has the cardinal number Doof the continuum. For the class of all ordered pairs of positive integers is of cardinal number* Mo- Therefore the set P of all classes of ordered pairs of positive integers is of cardinal numb ...
... Theorem 1. The class of all well-ordered rearrangements of the positive integers has the cardinal number Doof the continuum. For the class of all ordered pairs of positive integers is of cardinal number* Mo- Therefore the set P of all classes of ordered pairs of positive integers is of cardinal numb ...
Prime, Composite, Divisibility and Square Numbers
... 3. If the number has more than two factors, then it is composite. The above procedure works very well for small numbers. However, it would be time-consuming to find all factors of 621. Thus we need a better method for determining if a large number is prime or composite. Every number has one and itse ...
... 3. If the number has more than two factors, then it is composite. The above procedure works very well for small numbers. However, it would be time-consuming to find all factors of 621. Thus we need a better method for determining if a large number is prime or composite. Every number has one and itse ...
Prime, Composite, Divisibility and Square Numbers
... We can test for divisibility by 3 to quickly find a factor of 621 other than 1 and itself. The sum of the digits of 621 is 6+2+1 = 9. This divisibility test and the definitions above tell us that... * 621 is divisible by 3 since the sum of its digits (9) is divisible by 3. * Since 621 is divisible b ...
... We can test for divisibility by 3 to quickly find a factor of 621 other than 1 and itself. The sum of the digits of 621 is 6+2+1 = 9. This divisibility test and the definitions above tell us that... * 621 is divisible by 3 since the sum of its digits (9) is divisible by 3. * Since 621 is divisible b ...
Prime, Composite, Divisibility and Square Numbers
... If one whole number is divisible by another number, then the second number is a factor of the first number. Since 18 is divisible by 9, 9 is a factor of 18. A divisibility test is a rule for determining whether one whole number is divisible by another. It is a quick way to find factors of large numb ...
... If one whole number is divisible by another number, then the second number is a factor of the first number. Since 18 is divisible by 9, 9 is a factor of 18. A divisibility test is a rule for determining whether one whole number is divisible by another. It is a quick way to find factors of large numb ...
To test whether a fraction is in lowest terms, you need to know the
... 11—A number is divisible by 11 if the alternating sum of the digits is divisible by 11. Ex. To check if 65432532 is divisible by 11 look at 6-5+4-3+2-5+3-2=0. Since 0 is divisible by 11 (11 goes into 0 zero times) 65432532 is divisible by 0 also. You can stop when you get to the square root of a num ...
... 11—A number is divisible by 11 if the alternating sum of the digits is divisible by 11. Ex. To check if 65432532 is divisible by 11 look at 6-5+4-3+2-5+3-2=0. Since 0 is divisible by 11 (11 goes into 0 zero times) 65432532 is divisible by 0 also. You can stop when you get to the square root of a num ...
a special social security number
... Example 2. 76,448 is divisible by 8 since 48 is divisible by 8. How to tell if a number is divisible by 9: This test is similar to the divisibility test for 3. If you add up all the digits of the number and the sum of the digits is divisible by 9, then the number is divisible by 9. Example 1. Let’s ...
... Example 2. 76,448 is divisible by 8 since 48 is divisible by 8. How to tell if a number is divisible by 9: This test is similar to the divisibility test for 3. If you add up all the digits of the number and the sum of the digits is divisible by 9, then the number is divisible by 9. Example 1. Let’s ...
Divisibility Test
... To test 1595: the sum of odd digits = 1+9=10 the sum of even digits=5+5=10 the difference=10-10=0, so 1595 is divisible by 11. To test 23871903: the sum of odd =2+8+1+0=11, the sum of even =3+7+9+3=22, the difference= 22-11=11, So, 23871903 is divisible by 11. ...
... To test 1595: the sum of odd digits = 1+9=10 the sum of even digits=5+5=10 the difference=10-10=0, so 1595 is divisible by 11. To test 23871903: the sum of odd =2+8+1+0=11, the sum of even =3+7+9+3=22, the difference= 22-11=11, So, 23871903 is divisible by 11. ...
1 5 Divisibility Rules
... A number is divisible by 4 if the tens and ones digits form a number that is divisible by 4. Example: 47,836 is divisible by 4 because 36 is divisible by 4. It isn’t always easy to tell whether the last two digits form a number that is divisible by 4. A quick way to check is to divide the number by ...
... A number is divisible by 4 if the tens and ones digits form a number that is divisible by 4. Example: 47,836 is divisible by 4 because 36 is divisible by 4. It isn’t always easy to tell whether the last two digits form a number that is divisible by 4. A quick way to check is to divide the number by ...
Divisibility Rules Poster
... d. all of the above 4. Which of the following numbers is divisible by 6? a. 644 b. 4160 c. 5700 d. none of the above 5. If a number is divisible by 9, then it is also divisible by which number? a. 2 b. 3 c. 6 d. none of the above 6. Which of the following numbers have only one of the Divisibility Ru ...
... d. all of the above 4. Which of the following numbers is divisible by 6? a. 644 b. 4160 c. 5700 d. none of the above 5. If a number is divisible by 9, then it is also divisible by which number? a. 2 b. 3 c. 6 d. none of the above 6. Which of the following numbers have only one of the Divisibility Ru ...
Divisibility Rules - hrsbstaff.ednet.ns.ca
... divisible by six because it is even, so it is divisible by two and its digits add up to six, which makes it divisible by three Nine (9) A number is divisible by nine if the sum of the digits adds up to a multiple of nine. This rule is similar to the divisibility rule for three. 9243 is divisible by ...
... divisible by six because it is even, so it is divisible by two and its digits add up to six, which makes it divisible by three Nine (9) A number is divisible by nine if the sum of the digits adds up to a multiple of nine. This rule is similar to the divisibility rule for three. 9243 is divisible by ...
divisibility rules - Biblical Christian World View
... Since division is the inverse of multiplication, we can check a division problem using multiplication. The dividend will be equal to the product of the divisor and the quotient, plus the remainder. Now we can define divisibility with more accuracy. A number is said to be divisible by another number ...
... Since division is the inverse of multiplication, we can check a division problem using multiplication. The dividend will be equal to the product of the divisor and the quotient, plus the remainder. Now we can define divisibility with more accuracy. A number is said to be divisible by another number ...
Divisibility Rules - HRSBSTAFF Home Page
... From the divisibility rule for 5 we know the number must end in a 5 or 0. From the divisibility rule for 9 we know the sum of the digits must be divisible by 9. If we guess the last digit is 0 then the first digit or first two digits must add to 9. 90 does not work because the number must be great ...
... From the divisibility rule for 5 we know the number must end in a 5 or 0. From the divisibility rule for 9 we know the sum of the digits must be divisible by 9. If we guess the last digit is 0 then the first digit or first two digits must add to 9. 90 does not work because the number must be great ...
Characteristic of number Number divisible by
... How can you tell whether a number is divisible by another number (leaving no remainder) without actually doing the division? Why do "divisibility rules" work? For examples and explanations, see Divisibility Rules. Divisibility by: 2 If the last digit is even, the number is divisible by 2. 3 If the s ...
... How can you tell whether a number is divisible by another number (leaving no remainder) without actually doing the division? Why do "divisibility rules" work? For examples and explanations, see Divisibility Rules. Divisibility by: 2 If the last digit is even, the number is divisible by 2. 3 If the s ...
Divisibility Rules - York Catholic District School Board
... the last digit, double it, and subtract it from the rest of the number; if the answer is divisible by 7 (including 0), then the number is also. Ex: 672 (Double 2 is 4, 67- 4 = 63, and 63 ÷ 7 = 9) Yes {OR continue: double 3 = 6. 6 – 6 = 0) 905 (Double 5 is 10, 90 - 10 = 80, and 80 ÷ 7= 11 3/7) No Ex: ...
... the last digit, double it, and subtract it from the rest of the number; if the answer is divisible by 7 (including 0), then the number is also. Ex: 672 (Double 2 is 4, 67- 4 = 63, and 63 ÷ 7 = 9) Yes {OR continue: double 3 = 6. 6 – 6 = 0) 905 (Double 5 is 10, 90 - 10 = 80, and 80 ÷ 7= 11 3/7) No Ex: ...
The factorization of the ninth Fermat number
... and Cunninghamnumbers implies that these numbers are losing their value as a yardstickto measure progressin factoring. One wonders which class of numbers will take their place. Good test numbers for factoring algorithms should meet several conditions. They should be defined a priori, to avoid the im ...
... and Cunninghamnumbers implies that these numbers are losing their value as a yardstickto measure progressin factoring. One wonders which class of numbers will take their place. Good test numbers for factoring algorithms should meet several conditions. They should be defined a priori, to avoid the im ...
Class VI Chapter 3 – Playing with Numbers Maths Exercise 3.1
... Therefore, the largest number is 9. Question 6: Write a digit in the blank space of each of the following numbers so that the number formed is divisible by 11: (a) 92 ___ 389 (b) 8 ___9484 Answer: (a) 92_389 Let a be placed in the blank. Sum of the digits at odd places = 9 + 3 + 2 = 14 Sum of the di ...
... Therefore, the largest number is 9. Question 6: Write a digit in the blank space of each of the following numbers so that the number formed is divisible by 11: (a) 92 ___ 389 (b) 8 ___9484 Answer: (a) 92_389 Let a be placed in the blank. Sum of the digits at odd places = 9 + 3 + 2 = 14 Sum of the di ...
Which of the following are factors of 3,435,864? 2 3 4 5 6 8 9 10
... What is the smallest positive integer that is divisible by 2 and 3 that consists entirely of 2’s and 3’s, with at least one of each? ...
... What is the smallest positive integer that is divisible by 2 and 3 that consists entirely of 2’s and 3’s, with at least one of each? ...
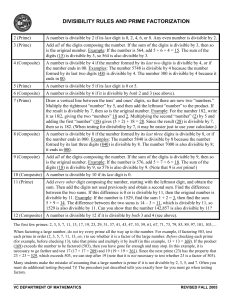
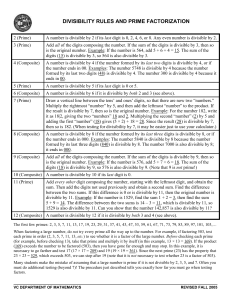
DIVISIBILITY RULES AND PRIME FACTORIZATION
... the result is divisible by 7, then so is the original number. Example: For the number 182, write it as 18|2, giving the two “numbers” 18 and 2. Multiplying the second “number” (2) by 5 and adding the first “number” (18) gives (5 × 2) + 18 = 28. Since the result (28) is divisible by 7, then so is 182 ...
... the result is divisible by 7, then so is the original number. Example: For the number 182, write it as 18|2, giving the two “numbers” 18 and 2. Multiplying the second “number” (2) by 5 and adding the first “number” (18) gives (5 × 2) + 18 = 28. Since the result (28) is divisible by 7, then so is 182 ...
Divisibility Rules
... the result is divisible by 7, then so is the original number. Example: For the number 182, write it as 18|2, giving the two “numbers” 18 and 2. Multiplying the second “number” (2) by 5 and adding the first “number” (18) gives (5 × 2) + 18 = 28. Since the result (28) is divisible by 7, then so is 182 ...
... the result is divisible by 7, then so is the original number. Example: For the number 182, write it as 18|2, giving the two “numbers” 18 and 2. Multiplying the second “number” (2) by 5 and adding the first “number” (18) gives (5 × 2) + 18 = 28. Since the result (28) is divisible by 7, then so is 182 ...
g1a place value visualized
... simple example is the number 14. The last numeral in 14, the 4, means 4 units. The preceding numeral, the 1, means 1 group of ten. In the number 24 (which we read as “twenty four”), the last numeral again means 4 units, and the preceding numeral, 2, means 2 groups of ten each. It is precisely becaus ...
... simple example is the number 14. The last numeral in 14, the 4, means 4 units. The preceding numeral, the 1, means 1 group of ten. In the number 24 (which we read as “twenty four”), the last numeral again means 4 units, and the preceding numeral, 2, means 2 groups of ten each. It is precisely becaus ...
HoMProblem1_solution
... j) But how do we prove that this answer is correct? Note: Examples may convince us, but they do not constitute a proof. Here is one way we can prove the statement. Note that the number of odd numbers in a row is equal to the row number. We can use this information to “count” how many odd numbers occ ...
... j) But how do we prove that this answer is correct? Note: Examples may convince us, but they do not constitute a proof. Here is one way we can prove the statement. Note that the number of odd numbers in a row is equal to the row number. We can use this information to “count” how many odd numbers occ ...
Divisibility Rules
... know what it is? Try the following problem: 2 0. Since division is the opposite of multiplication, this is the same as asking, “What number times 0 will equal 2?” Any number multiplied by 0 is equal to 0, so it’s impossible to have a number that, when multiplied by 0, will equal 2.That’s why 2 0 rea ...
... know what it is? Try the following problem: 2 0. Since division is the opposite of multiplication, this is the same as asking, “What number times 0 will equal 2?” Any number multiplied by 0 is equal to 0, so it’s impossible to have a number that, when multiplied by 0, will equal 2.That’s why 2 0 rea ...
Divisibility - Dalton State
... • Double the ones digit and subtract from the remaining digits • If that number is equal to zero or divisible by 7, then the original number is • If your number is still a big number, repeat the process ...
... • Double the ones digit and subtract from the remaining digits • If that number is equal to zero or divisible by 7, then the original number is • If your number is still a big number, repeat the process ...