
Reading Dimensions Using a Standard Ruler
... The physical shape of an object is shown • object lines • hidden lines ...
... The physical shape of an object is shown • object lines • hidden lines ...
Interactive Hierarchical Dimension Ordering, Spacing and Filtering
... can have a major impact on the expressiveness of the visualization because the relationships among adjacent dimensions are easier to detect than relationships among dimensions positioned far from each other. Another example is attribute mapping. In visualizations such as Chernoff Faces [Chernoff 197 ...
... can have a major impact on the expressiveness of the visualization because the relationships among adjacent dimensions are easier to detect than relationships among dimensions positioned far from each other. Another example is attribute mapping. In visualizations such as Chernoff Faces [Chernoff 197 ...
Dual Shattering Dimension
... conclusion might not hold (This is of course true). In real applications we use a much larger sample to guarantee that the probability of failure is so small that it can be practically ignored. A more serious issue is that Theorem 5.28 is defined only for finite sets. No where does it speak ab ...
... conclusion might not hold (This is of course true). In real applications we use a much larger sample to guarantee that the probability of failure is so small that it can be practically ignored. A more serious issue is that Theorem 5.28 is defined only for finite sets. No where does it speak ab ...
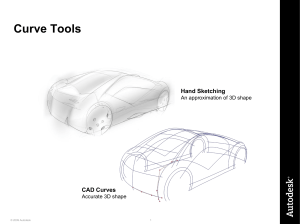
Why Use Curves? - cloudfront.net
... EX1-Curves.wire EX2-Curves-circles.wire EX3-Car-curves.wire EX4-Symmetrical-curves.wire EX5-Flatten-circle.wire ...
... EX1-Curves.wire EX2-Curves-circles.wire EX3-Car-curves.wire EX4-Symmetrical-curves.wire EX5-Flatten-circle.wire ...
On Cantorian spacetime over number systems with division by zero
... language for physics, and physical reality cannot be deduced from a priori philosophical concepts [5], therefore mathematics may need an upgrade after a discovery is made in physics, for some old ideas may be irrelevant to new aspects of the physical reality. We need a synthetic mathematics (SM) to ...
... language for physics, and physical reality cannot be deduced from a priori philosophical concepts [5], therefore mathematics may need an upgrade after a discovery is made in physics, for some old ideas may be irrelevant to new aspects of the physical reality. We need a synthetic mathematics (SM) to ...
Chapter 6 Proportions and Similarity
... » The Triangle: If you connect the midpoints of the sides of an equilateral triangle, it’ll form a smaller triangle. In the three triangular spaces, you can create more triangles by repeating the process, indefinitely. This example of a fractal (geometric figure created by iteration, or repeating th ...
... » The Triangle: If you connect the midpoints of the sides of an equilateral triangle, it’ll form a smaller triangle. In the three triangular spaces, you can create more triangles by repeating the process, indefinitely. This example of a fractal (geometric figure created by iteration, or repeating th ...
Special Angles on Parallel Lines
... Some picture patterns are also generated by recursive rules. You find the next picture in the sequence by looking at the picture before it and comparing that to the picture before it, and so on. The Geometer’s Sketchpad® can repeat a recursive rule on a figure using a command called Iterate. Using I ...
... Some picture patterns are also generated by recursive rules. You find the next picture in the sequence by looking at the picture before it and comparing that to the picture before it, and so on. The Geometer’s Sketchpad® can repeat a recursive rule on a figure using a command called Iterate. Using I ...
[edit] Construction of the Lebesgue measure
... An early paper by Benoit Mandelbrot entitled How Long Is the Coast of Britain? Statistical SelfSimilarity and Fractional Dimension and subsequent work by other authors have claimed that the Hausdorff dimension of many coastlines can be estimated. Their results have varied from 1.02 for the coastline ...
... An early paper by Benoit Mandelbrot entitled How Long Is the Coast of Britain? Statistical SelfSimilarity and Fractional Dimension and subsequent work by other authors have claimed that the Hausdorff dimension of many coastlines can be estimated. Their results have varied from 1.02 for the coastline ...
Fractal Geometry: The Mandelbrot and Julia Sets
... The Mandelbrot set is a set of values c ∈ C with certain important properties. We will examine the formal definition of the set as well as many of its interesting, strange, and beautiful properties. The Mandelbrot set is most well known outside of mathematics as a set of beautiful images of fractals ...
... The Mandelbrot set is a set of values c ∈ C with certain important properties. We will examine the formal definition of the set as well as many of its interesting, strange, and beautiful properties. The Mandelbrot set is most well known outside of mathematics as a set of beautiful images of fractals ...
Fractal in the statistics of Goldbach partition 1 Introduction
... [Abstract] Some interesting chaos phenomena have been found in the difference of prime numbers. Here we discuss a theme about the sum of two prime numbers, Goldbach conjecture. This conjecture states that any even number could be expressed as the sum of two prime numbers. Goldbach partition r(n) is ...
... [Abstract] Some interesting chaos phenomena have been found in the difference of prime numbers. Here we discuss a theme about the sum of two prime numbers, Goldbach conjecture. This conjecture states that any even number could be expressed as the sum of two prime numbers. Goldbach partition r(n) is ...
Teacher Talk-Standards behind Reasoning
... relationships within, an axiomatic system. • (B)recognize the historical development of geometric systems and know mathematics is developed for a variety of purposes; and • (C)compare and contrast the structures and implications of Euclidean and non-Euclidean geometries. ...
... relationships within, an axiomatic system. • (B)recognize the historical development of geometric systems and know mathematics is developed for a variety of purposes; and • (C)compare and contrast the structures and implications of Euclidean and non-Euclidean geometries. ...
Full text
... THE FIBONACCI QUARTERLY According to Theorem 1, any s and x that do not eventually doubly intersperse must eventually intersperse, and one should surely then ask “where the interspersion commences.” A practical way to answer this question for given specific sequences is to determine the least i for ...
... THE FIBONACCI QUARTERLY According to Theorem 1, any s and x that do not eventually doubly intersperse must eventually intersperse, and one should surely then ask “where the interspersion commences.” A practical way to answer this question for given specific sequences is to determine the least i for ...
infinite perimeter of the Koch snowflake and its finite - Dimes
... answers to questions regarding fractals (calculation of, e.g., their length, area, volume or the number of smaller copies of initiators present at the n-th iteration) only for finite values of n. The same questions very often remain without any answer when we consider an infinite number of steps bec ...
... answers to questions regarding fractals (calculation of, e.g., their length, area, volume or the number of smaller copies of initiators present at the n-th iteration) only for finite values of n. The same questions very often remain without any answer when we consider an infinite number of steps bec ...
Reporting Category 2
... On the map below, First Avenue and Second Avenue are parallel. A city planner proposes to locate a small garden and park on the triangular island by the intersections of four streets shown. A. 90°, 65°, 25° B. 90°, 50°, 40° C. 90°, 60°, 30° D. 130°, 40°, 10° ...
... On the map below, First Avenue and Second Avenue are parallel. A city planner proposes to locate a small garden and park on the triangular island by the intersections of four streets shown. A. 90°, 65°, 25° B. 90°, 50°, 40° C. 90°, 60°, 30° D. 130°, 40°, 10° ...
Flatland 2: Sphereland
... Flatland dismiss the idea of the third dimension. But when a scientist (Danny Pudi) discovers a mathematical anomaly, he turns to the only person who might listen - Hex (Kristen Bell), an outcast mathematician shunned for her ideas of the third dimension. An unexpected reunion with Spherius (Michael ...
... Flatland dismiss the idea of the third dimension. But when a scientist (Danny Pudi) discovers a mathematical anomaly, he turns to the only person who might listen - Hex (Kristen Bell), an outcast mathematician shunned for her ideas of the third dimension. An unexpected reunion with Spherius (Michael ...
6-1 Proportions Ratio—a comparison of two quantities Proportion
... Theorem 6.7 Proportional Perimeters Theorem If two triangles are similar, then the perimeters are proportional to the measures of corresponding sides. Theorem 6.8 If two triangles are similar, then the measures of the corresponding altitudes are proportional to the measures of the corresponding side ...
... Theorem 6.7 Proportional Perimeters Theorem If two triangles are similar, then the perimeters are proportional to the measures of corresponding sides. Theorem 6.8 If two triangles are similar, then the measures of the corresponding altitudes are proportional to the measures of the corresponding side ...
Hyperbolic spaces from self-similar group actions
... and from the point of view of many other fields of mathematics (operator algebras, holomorphic dynamics, automata theory, etc). See the works [BGN02, GNS00, Gri00, Sid98, BG00, Nek02a], where different aspects of self-similar groups are studied. An important class of self-similar group actions are c ...
... and from the point of view of many other fields of mathematics (operator algebras, holomorphic dynamics, automata theory, etc). See the works [BGN02, GNS00, Gri00, Sid98, BG00, Nek02a], where different aspects of self-similar groups are studied. An important class of self-similar group actions are c ...
Sixty Years of Fractal Projections arXiv
... was heavily influenced by Abram Besicovitch, a Russian born mathematician who pioneered geometric measure theory. For 25 years after its publication the paper attracted very limited attention, since then it has become one of the most frequently cited papers in the area now referred to as fractal geo ...
... was heavily influenced by Abram Besicovitch, a Russian born mathematician who pioneered geometric measure theory. For 25 years after its publication the paper attracted very limited attention, since then it has become one of the most frequently cited papers in the area now referred to as fractal geo ...
Title of the Paper (18pt Times New Roman, Bold)
... The result of this algorithm is an image of coloured pixels. This image, shown in Figure 2 can describe a distant astronomical object like a nebula or galaxy of stars. It can also suggest a fireball from an explosion. Marek Wolf, who has also detected some connections between prime number distributi ...
... The result of this algorithm is an image of coloured pixels. This image, shown in Figure 2 can describe a distant astronomical object like a nebula or galaxy of stars. It can also suggest a fireball from an explosion. Marek Wolf, who has also detected some connections between prime number distributi ...
Junior - CEMC - University of Waterloo
... side of the main stem. These leaves once again have groups of leaves branching off of a main stem. Even the smallest size leaves we can see on the fern have a bumpy shape that is similar to the entire fern. What are other examples of fractals in nature? blood vessels, broccoli, mountain ranges, naut ...
... side of the main stem. These leaves once again have groups of leaves branching off of a main stem. Even the smallest size leaves we can see on the fern have a bumpy shape that is similar to the entire fern. What are other examples of fractals in nature? blood vessels, broccoli, mountain ranges, naut ...
Sixth Form Area and Perimeter
... Further ideas Overview The relation between the perimeter of closed curves (in a 2d plane) and the area enclosed by them is not straightforward. There are two classic results. I. For planar regions of fixed area (say 1 square unit), the circle is the shape with minimum perimeter. II. On the other ha ...
... Further ideas Overview The relation between the perimeter of closed curves (in a 2d plane) and the area enclosed by them is not straightforward. There are two classic results. I. For planar regions of fixed area (say 1 square unit), the circle is the shape with minimum perimeter. II. On the other ha ...
Sixth Form Area and Perimeter
... starting point for a discussion on area and perimeter. 2. Is it possible to cut a hole in a 1p sized circle so that a 2p coin can go through it? Is it possible for you to cut a hole in an A4 size sheet of paper and walk right through that hole? If no, explain why. If yes, cut such a hole and demonst ...
... starting point for a discussion on area and perimeter. 2. Is it possible to cut a hole in a 1p sized circle so that a 2p coin can go through it? Is it possible for you to cut a hole in an A4 size sheet of paper and walk right through that hole? If no, explain why. If yes, cut such a hole and demonst ...
Intersecting Two-Dimensional Fractals with Lines Shigeki Akiyama
... we will show that the intersection with the negative real axis has infinitely many components (Theorem 3.9). To prove this, we use the special structure of this fractal set. The idea is to find a contractive map around −1 which preserves the local structure. We expect results of similar type for the ...
... we will show that the intersection with the negative real axis has infinitely many components (Theorem 3.9). To prove this, we use the special structure of this fractal set. The idea is to find a contractive map around −1 which preserves the local structure. We expect results of similar type for the ...
Recursion - inst.eecs.berkeley.edu
... ● the same logic applies for this Snap version ● factorial (5) = 5 x factorial (4) = 5 x 4 x factorial (3), and etc. ● the recursion finally ends at factorial (1), when our block just reports 1, not calling itself again ...
... ● the same logic applies for this Snap version ● factorial (5) = 5 x factorial (4) = 5 x 4 x factorial (3), and etc. ● the recursion finally ends at factorial (1), when our block just reports 1, not calling itself again ...
Recursion - EECS: www-inst.eecs.berkeley.edu
... ● the same logic applies for this Snap version ● factorial (5) = 5 x factorial (4) = 5 x 4 x factorial (3), and etc. ● the recursion finally ends at factorial (1), when our block just reports 1, not calling itself again ...
... ● the same logic applies for this Snap version ● factorial (5) = 5 x factorial (4) = 5 x 4 x factorial (3), and etc. ● the recursion finally ends at factorial (1), when our block just reports 1, not calling itself again ...
Fractal

A fractal is a natural phenomenon or a mathematical set that exhibits a repeating pattern that displays at every scale. If the replication is exactly the same at every scale, it is called a self-similar pattern. An example of this is the Menger Sponge. Fractals can also be nearly the same at different levels. This latter pattern is illustrated in the magnifications of the Mandelbrot set. Fractals also include the idea of a detailed pattern that repeats itself.Fractals are different from other geometric figures because of the way in which they scale. Doubling the edge lengths of a polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the dimension of the space the polygon resides in). Likewise, if the radius of a sphere is doubled, its volume scales by eight, which is two (the ratio of the new to the old radius) to the power of three (the dimension that the sphere resides in). But if a fractal's one-dimensional lengths are all doubled, the spatial content of the fractal scales by a power that is not necessarily an integer. This power is called the fractal dimension of the fractal, and it usually exceeds the fractal's topological dimension.As mathematical equations, fractals are usually nowhere differentiable. An infinite fractal curve can be conceived of as winding through space differently from an ordinary line, still being a 1-dimensional line yet having a fractal dimension indicating it also resembles a surface.The mathematical roots of the idea of fractals have been traced throughout the years as a formal path of published works, starting in the 17th century with notions of recursion, then moving through increasingly rigorous mathematical treatment of the concept to the study of continuous but not differentiable functions in the 19th century, and on to the coining of the word fractal in the 20th century with a subsequent burgeoning of interest in fractals and computer-based modelling in the 21st century. The term ""fractal"" was first used by mathematician Benoît Mandelbrot in 1975. Mandelbrot based it on the Latin frāctus meaning ""broken"" or ""fractured"", and used it to extend the concept of theoretical fractional dimensions to geometric patterns in nature.There is some disagreement amongst authorities about how the concept of a fractal should be formally defined. Mandelbrot himself summarized it as ""beautiful, damn hard, increasingly useful. That's fractals."" The general consensus is that theoretical fractals are infinitely self-similar, iterated, and detailed mathematical constructs having fractal dimensions, of which many examples have been formulated and studied in great depth. Fractals are not limited to geometric patterns, but can also describe processes in time. Fractal patterns with various degrees of self-similarity have been rendered or studied in images, structures and sounds and found in nature, technology, art, and law.





![[edit] Construction of the Lebesgue measure](http://s1.studyres.com/store/data/001141507_1-534aa5aeea25b32a8226835f0ebc16e0-300x300.png)
















