Current-induced magnetic vortex motion by spin
... of which magnetization is assumed to be constant. The dimension of the cells is 4 ⫻ 4 ⫻ h nm3 with dot thickness h = 10, 20, 30 nm. The dot radius is taken to be R = 500 nm. The computational material parameters are typical for permalloy: M s = 1.0 T 共M s / 0 = 8.0⫻ 105 A / m兲, the exchange stiffne ...
... of which magnetization is assumed to be constant. The dimension of the cells is 4 ⫻ 4 ⫻ h nm3 with dot thickness h = 10, 20, 30 nm. The dot radius is taken to be R = 500 nm. The computational material parameters are typical for permalloy: M s = 1.0 T 共M s / 0 = 8.0⫻ 105 A / m兲, the exchange stiffne ...
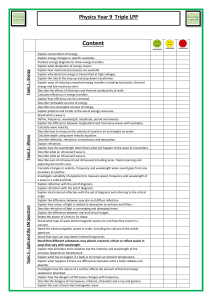
chap. 9
... Both the block and the steel object are in equilibrium. Thus, the sum of the buoyant force on the steel object and the tension in the string must equal the weight of the steel object, so this buoyant force and the tension in the string must each be less than the weight of the object. The buoyant for ...
... Both the block and the steel object are in equilibrium. Thus, the sum of the buoyant force on the steel object and the tension in the string must equal the weight of the steel object, so this buoyant force and the tension in the string must each be less than the weight of the object. The buoyant for ...
6.8A Potential Kinetic Energy
... Potential energy is stored energy—energy ready to go. A lawn mower filled with gasoline, a car on top of a hill, and students waiting to go home from school are all examples of potential energy. Water stored behind a dam at a hydroelectric plant has potential energy. Most of the energy under our con ...
... Potential energy is stored energy—energy ready to go. A lawn mower filled with gasoline, a car on top of a hill, and students waiting to go home from school are all examples of potential energy. Water stored behind a dam at a hydroelectric plant has potential energy. Most of the energy under our con ...
The Modified Theory of Central-Force Motion Edison A. Enaibe,(Ph.D.)
... constraints which may be imposed is called the number of degrees of freedom of the system. The number of degrees of freedom is the number of quantities which must be specified in order to determine the velocities of all particles in the system for any motion which does not violate the constraints [4 ...
... constraints which may be imposed is called the number of degrees of freedom of the system. The number of degrees of freedom is the number of quantities which must be specified in order to determine the velocities of all particles in the system for any motion which does not violate the constraints [4 ...
Chapter 4 Test.final A
... constant velocity to increase its speed in that direction. c. A cart is moving at a constant velocity of 10 m/s [W] when a 0.5 N [downward] force is applied. d. The work done by Earth on an arrow as it is fired 200 m straight up into the air. e. Earth applies a force on the Moon as the Moon travels ...
... constant velocity to increase its speed in that direction. c. A cart is moving at a constant velocity of 10 m/s [W] when a 0.5 N [downward] force is applied. d. The work done by Earth on an arrow as it is fired 200 m straight up into the air. e. Earth applies a force on the Moon as the Moon travels ...
A toroidal momentum pinch velocity due to the Coriolis drift effect on
... will be largely absent in a fusion reactor, it is generally assumed that the rotation, and hence its positive influence, will be small. The pinch velocity described in this letter, however, may generate a sizeable toroidal velocity gradient even in the absence of a torque. The physics effect generat ...
... will be largely absent in a fusion reactor, it is generally assumed that the rotation, and hence its positive influence, will be small. The pinch velocity described in this letter, however, may generate a sizeable toroidal velocity gradient even in the absence of a torque. The physics effect generat ...
B. Picchetti
... , where 2.3.2 was recalled. P equals the product of the rolling force times the tangential velocity. This equals the rolling length times the roller angular velocity ...
... , where 2.3.2 was recalled. P equals the product of the rolling force times the tangential velocity. This equals the rolling length times the roller angular velocity ...
Department of Physics and Applied Physics 95.141, S2010, Lecture 23
... • If I let the pendulum swing, would it keep returning to the same original displacement? • In the real world there are other forces, in addition to the restoring force which act on the pendulum (or any oscillator). • The harmonic motion for these real-world oscillators is no longer simple. • Damped ...
... • If I let the pendulum swing, would it keep returning to the same original displacement? • In the real world there are other forces, in addition to the restoring force which act on the pendulum (or any oscillator). • The harmonic motion for these real-world oscillators is no longer simple. • Damped ...
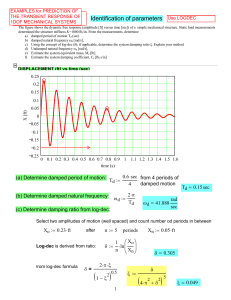
(ft) vs time (sec)
... The car of mass M=500 kg is traveling at constant speed Vo= 50 kilometer/hour when it hits a rigid wall. A spring (K) and a viscous dashpot (C) represent the car front bumper system. The system natural frequency fn=3 Hz, and the dashpot provides critical damping. Disregard friction on the car wheels ...
... The car of mass M=500 kg is traveling at constant speed Vo= 50 kilometer/hour when it hits a rigid wall. A spring (K) and a viscous dashpot (C) represent the car front bumper system. The system natural frequency fn=3 Hz, and the dashpot provides critical damping. Disregard friction on the car wheels ...
unit 21: electrical and gravitational potential
... Work and the Electric Field It takes work to lift an object in the earth's gravitational field. Lowering the object releases the energy that was stored as potential energy when it was lifted. Last semester, we applied the term conservative to the gravitational force because it "releases" all of the ...
... Work and the Electric Field It takes work to lift an object in the earth's gravitational field. Lowering the object releases the energy that was stored as potential energy when it was lifted. Last semester, we applied the term conservative to the gravitational force because it "releases" all of the ...











![[2015 question paper]](http://s1.studyres.com/store/data/008881819_1-2322a19bdc6e8ffedff685bb2aff8c48-300x300.png)