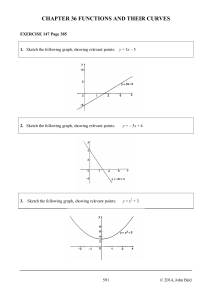
CHAPTER 36 FUNCTIONS AND THEIR CURVES
... Equating the coefficient of the highest power of x (i.e. x 3 in this case) gives 1 – m 2 = 0, from which, m=±1 Equating the coefficient of the next highest power of x (i.e. x 2 in this case) gives –2mc = 0, from which, c = 0 Hence y = mx + c = ± 1x + 0, i.e. y = x and y = –x are asymptotes To determ ...
... Equating the coefficient of the highest power of x (i.e. x 3 in this case) gives 1 – m 2 = 0, from which, m=±1 Equating the coefficient of the next highest power of x (i.e. x 2 in this case) gives –2mc = 0, from which, c = 0 Hence y = mx + c = ± 1x + 0, i.e. y = x and y = –x are asymptotes To determ ...







![[3] body chapter 7](http://s1.studyres.com/store/data/005887247_1-60b3de506642a2c722a312b36e081828-300x300.png)