A NOTE ON DERIVATIONS OF COMMUTATIVE ALGEBRAS 1199
... +wxD can be written in operator form as R^ = (Rx, D), where Ru denotes the mapping a—*au of C, so that trace 7?x£>= 0 for all xEC. Moreover, trace Rw = 0 for all w in TV. For since C is commutative and w is nilpotent, 7?„ is nilpotent [3, Theorem 2], hence trace Rw = 0. Now suppose that x is an arbi ...
... +wxD can be written in operator form as R^ = (Rx, D), where Ru denotes the mapping a—*au of C, so that trace 7?x£>= 0 for all xEC. Moreover, trace Rw = 0 for all w in TV. For since C is commutative and w is nilpotent, 7?„ is nilpotent [3, Theorem 2], hence trace Rw = 0. Now suppose that x is an arbi ...
General history of algebra
... operation (there are negative number) • Multiplication isn’t necessarily commutative and it doesn’t have an inverse (there’s no division) • Multiplication distributes over addition • Examples: rationals, reals under these limits 3 (4 + 5) = 12 + 8, but 12 + 8 ≠ 8 + 12 ...
... operation (there are negative number) • Multiplication isn’t necessarily commutative and it doesn’t have an inverse (there’s no division) • Multiplication distributes over addition • Examples: rationals, reals under these limits 3 (4 + 5) = 12 + 8, but 12 + 8 ≠ 8 + 12 ...
Algebras
... Remark also that A has, a priori, no unit. Proposition & Definition 1.1.3 Let A be an algebra, the vector space A together with the multiplication defined by (x, y) 7→ yx is again an algebra called the opposite algebra and denoted Aop . Proposition & Definition 1.1.4 A subvector space B of A which i ...
... Remark also that A has, a priori, no unit. Proposition & Definition 1.1.3 Let A be an algebra, the vector space A together with the multiplication defined by (x, y) 7→ yx is again an algebra called the opposite algebra and denoted Aop . Proposition & Definition 1.1.4 A subvector space B of A which i ...
Chapter 7 Spectral Theory Of Linear Operators In Normed Spaces
... 7.6-3 Space R and C. The real line and the complex plane C are commutative Banach algebra with identity e = 1. 7.6-4 Space C[a, b]. The space C[a, b] is a commutative Banach algebra with identity e = 1, the product xy being defined as usual (xy)(t) = x(t)y(t) for all tC[a, b] and the norm is the ma ...
... 7.6-3 Space R and C. The real line and the complex plane C are commutative Banach algebra with identity e = 1. 7.6-4 Space C[a, b]. The space C[a, b] is a commutative Banach algebra with identity e = 1, the product xy being defined as usual (xy)(t) = x(t)y(t) for all tC[a, b] and the norm is the ma ...
Lecture 8 - Universal Enveloping Algebras and Related Concepts, II
... Following Humphreys, we give a few fundamental corollaries along with their proofs. Corollary 2.3 Assume W ⊆ T m g is a vector subspace, and that the canonical projection T g → Sg sends W isomorphically onto S m g. Then πT (W ) is a compliment to U (m−1) (g) in U (m) (g). Pf. The following diagram o ...
... Following Humphreys, we give a few fundamental corollaries along with their proofs. Corollary 2.3 Assume W ⊆ T m g is a vector subspace, and that the canonical projection T g → Sg sends W isomorphically onto S m g. Then πT (W ) is a compliment to U (m−1) (g) in U (m) (g). Pf. The following diagram o ...
PDF
... It is this version of an element description of Jacobson radicals which can be generalized to non-associative algebras. First one must define homotopes and isotopes for the given non-associative algebra. Theorem 2 (McCrimmon, Jacobson). The radical of a Jordan algebra J is equivalently defined as: 1 ...
... It is this version of an element description of Jacobson radicals which can be generalized to non-associative algebras. First one must define homotopes and isotopes for the given non-associative algebra. Theorem 2 (McCrimmon, Jacobson). The radical of a Jordan algebra J is equivalently defined as: 1 ...
Exercises 5 5.1. Let A be an abelian group. Set A ∗ = HomZ(A,Q/Z
... 5.4. An algebra A over a field K is called a division algebra, if A is a division ring. Give an example of noncommutative division algebra over R. 5.5. Let K be a field, and A a K-linear space with a basis {xi }i∈I . Show that a bilinear map A × A → A, (a, b) 7→ a · b makes A an algebra (not necessa ...
... 5.4. An algebra A over a field K is called a division algebra, if A is a division ring. Give an example of noncommutative division algebra over R. 5.5. Let K be a field, and A a K-linear space with a basis {xi }i∈I . Show that a bilinear map A × A → A, (a, b) 7→ a · b makes A an algebra (not necessa ...
Chapter 1 Distance Adding Mixed Numbers Fractions of the same
... Fundementals of Algebra – p.10/16 ...
... Fundementals of Algebra – p.10/16 ...
ON THE NUMBER OF QUASI
... for i = 1, . . . , n. Then there is an unique extension of 2∗ to an operation 2 : A → A satisfying the equation (3) 2(x ∧ y) = 2x ∧ 2y (i.e. the resulting algebra is a quasi-modal algebra). Proof. If a < 1 in A then there are elements ck1 , . . . , ckm in CAt (uniquely determined by a) such that a = ...
... for i = 1, . . . , n. Then there is an unique extension of 2∗ to an operation 2 : A → A satisfying the equation (3) 2(x ∧ y) = 2x ∧ 2y (i.e. the resulting algebra is a quasi-modal algebra). Proof. If a < 1 in A then there are elements ck1 , . . . , ckm in CAt (uniquely determined by a) such that a = ...
INTRODUCTION TO C* ALGEBRAS - I Introduction : In this talk, we
... Introduction : In this talk, we introduce the notion of a C* algebra (a.k.a. Operator Algebra). The theory of C* algebras has its roots in functional analysis (where the basic object is a normed vector space). C* algebras provide an interesting place where analytic notions (such as limits and differ ...
... Introduction : In this talk, we introduce the notion of a C* algebra (a.k.a. Operator Algebra). The theory of C* algebras has its roots in functional analysis (where the basic object is a normed vector space). C* algebras provide an interesting place where analytic notions (such as limits and differ ...
4.4.
... vector space A over F with an additional operation AxA -> A. – (i) a(bc)=(ab)c. – (ii) a(b+c)=ab+ac,(a+b)c=ac+bc ,a,b,c in A. – (iii) c(ab)=(ca)b= a(cb), a,b in A, c in F – If there exists 1 in A s.t. a1=1a=a for all a in A, then A is a linear algebra with 1. – A is commutative if ab=ba for all a,b ...
... vector space A over F with an additional operation AxA -> A. – (i) a(bc)=(ab)c. – (ii) a(b+c)=ab+ac,(a+b)c=ac+bc ,a,b,c in A. – (iii) c(ab)=(ca)b= a(cb), a,b in A, c in F – If there exists 1 in A s.t. a1=1a=a for all a in A, then A is a linear algebra with 1. – A is commutative if ab=ba for all a,b ...
4.1,4.2
... vector space A over F with an additional operation AxA -> A. – (i) a(bc)=(ab)c. – (ii) a(b+c)=ab+ac,(a+b)c=ac+bc ,a,b,c in A. – (iii) c(ab)=(ca)b= a(cb), a,b in A, c in F – If there exists 1 in A s.t. a1=1a=a for all a in A, then A is a linear algebra with 1. – A is commutative if ab=ba for all a,b ...
... vector space A over F with an additional operation AxA -> A. – (i) a(bc)=(ab)c. – (ii) a(b+c)=ab+ac,(a+b)c=ac+bc ,a,b,c in A. – (iii) c(ab)=(ca)b= a(cb), a,b in A, c in F – If there exists 1 in A s.t. a1=1a=a for all a in A, then A is a linear algebra with 1. – A is commutative if ab=ba for all a,b ...
PDF
... In the foregoing discussion, an algebra shall mean a non-associative algebra. Let A be a normed ∗-algebra, an algebra admitting an involution ∗, over a commutative ring R with 1 6= 0. The Cayley-Dickson construction is a way of enlarging A to a new algebra, KD(A), extending the ∗ as well as the norm ...
... In the foregoing discussion, an algebra shall mean a non-associative algebra. Let A be a normed ∗-algebra, an algebra admitting an involution ∗, over a commutative ring R with 1 6= 0. The Cayley-Dickson construction is a way of enlarging A to a new algebra, KD(A), extending the ∗ as well as the norm ...
PDF
... The category of commutative Hopf algebras is anti-equivalent to the category of affine group schemes. The prime spectrum of a commutative Hopf algebra is an affine group scheme of multiplicative units. And going in the opposite direction, the algebra of natural transformations from an affine group s ...
... The category of commutative Hopf algebras is anti-equivalent to the category of affine group schemes. The prime spectrum of a commutative Hopf algebra is an affine group scheme of multiplicative units. And going in the opposite direction, the algebra of natural transformations from an affine group s ...
PDF
... is called the commutator bracket. The commutator bracket is bilinear, skew-symmetric, and also satisfies the Jacobi identity. To wit, for a, b, c ∈ A we have [a, [b, c]] + [b, [c, a]] + [c, [a, b]] = 0. The proof of this assertion is straightforward. Each of the brackets in the lefthand side expands ...
... is called the commutator bracket. The commutator bracket is bilinear, skew-symmetric, and also satisfies the Jacobi identity. To wit, for a, b, c ∈ A we have [a, [b, c]] + [b, [c, a]] + [c, [a, b]] = 0. The proof of this assertion is straightforward. Each of the brackets in the lefthand side expands ...
Math 461/561 Week 2 Solutions 1.7 Let L be a Lie algebra. The
... Thus φ is a Lie algebra homomorphism. (ii) Let (x, y) ∈ L1 ⊕ L2 . Then (x, y) ∈ Z(L1 ⊕ L2 ) if and only if [(x, y), (a, b)] = (0, 0) for all (a, b) ∈ L1 ⊕ L2 . But [(x, y), (a, b)] = ([x, a], [y, b]) so this is zero if and only if x ∈ Z(L1 ) and y ∈ Z(L2 ). Thus Z(L1 ⊕ L2 ) = Z(L1 ) ⊕ Z(L2 ). It is ...
... Thus φ is a Lie algebra homomorphism. (ii) Let (x, y) ∈ L1 ⊕ L2 . Then (x, y) ∈ Z(L1 ⊕ L2 ) if and only if [(x, y), (a, b)] = (0, 0) for all (a, b) ∈ L1 ⊕ L2 . But [(x, y), (a, b)] = ([x, a], [y, b]) so this is zero if and only if x ∈ Z(L1 ) and y ∈ Z(L2 ). Thus Z(L1 ⊕ L2 ) = Z(L1 ) ⊕ Z(L2 ). It is ...
Algebras. Derivations. Definition of Lie algebra
... saying [xx] = 0 is called anticommutativity. In fact, it implies that [xy] = −[yx] for all x, y. Proof: 0 = [x + y, x + y] = [xx] + [xy] + [yx] + [yy]. This implies [xy] = −[yx]. The converse is true if char k 6= 2. In fact, [xx] = −[xx] implies that 2[xx] = 0 and, if the charactersitic of k is not ...
... saying [xx] = 0 is called anticommutativity. In fact, it implies that [xy] = −[yx] for all x, y. Proof: 0 = [x + y, x + y] = [xx] + [xy] + [yx] + [yy]. This implies [xy] = −[yx]. The converse is true if char k 6= 2. In fact, [xx] = −[xx] implies that 2[xx] = 0 and, if the charactersitic of k is not ...
Coordinate Algebra - Georgia Department of Education
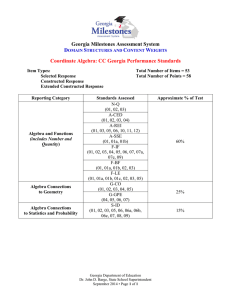
... Georgia Milestones Assessment System DOMAIN STRUCTURES AND CONTENT WEIGHTS Coordinate Algebra: CC Georgia Performance Standards Item Types: Selected Response Constructed Response Extended Constructed Response Reporting Category ...
... Georgia Milestones Assessment System DOMAIN STRUCTURES AND CONTENT WEIGHTS Coordinate Algebra: CC Georgia Performance Standards Item Types: Selected Response Constructed Response Extended Constructed Response Reporting Category ...
INTRODUCTION TO LIE ALGEBRAS. LECTURE 2. 2. More
... x, f (x), . . . , f t−1 (x) can be expressed as linear combinations of t linearly independent vectors xλ . The transition matrix has form ...
... x, f (x), . . . , f t−1 (x) can be expressed as linear combinations of t linearly independent vectors xλ . The transition matrix has form ...
PDF
... With these equations we can define certain subalgebras, for example we see both axioms at work in Proposition 2. Given an algebra A, the set Z0 (A) = {z ∈ A : za = az, a ∈ A}. Z0 (A) is a submodule of A. ...
... With these equations we can define certain subalgebras, for example we see both axioms at work in Proposition 2. Given an algebra A, the set Z0 (A) = {z ∈ A : za = az, a ∈ A}. Z0 (A) is a submodule of A. ...
PDF
... N (x) = (a + bk)(a − bk) = (aa + bb) + (−ba + ba)k = aa + bb ≥ 0. It is not hard to see that N (x) = 0 iff x = 0. ∗ hOctonioni ...
... N (x) = (a + bk)(a − bk) = (aa + bb) + (−ba + ba)k = aa + bb ≥ 0. It is not hard to see that N (x) = 0 iff x = 0. ∗ hOctonioni ...
Universal Enveloping Algebras (and
... Under bracket multiplication, Lie algebras are non-associative. The idea behind the construction of the universal enveloping algebra of some Lie algebra g is to pass from this non-associative object to its more friendly unital associative counterpart U g (allowing for the use of asociative methods s ...
... Under bracket multiplication, Lie algebras are non-associative. The idea behind the construction of the universal enveloping algebra of some Lie algebra g is to pass from this non-associative object to its more friendly unital associative counterpart U g (allowing for the use of asociative methods s ...
DERIVATIONS IN ALGEBRAS OF OPERATOR
... Consider an arbitrary semifinite von Neumann algebra M and the algebra S(M) of all measurable operators affiliated with M (the algebra S(M) was first introduced by I.E. Segal in 1953 and is a cornerstone of noncommutative integration theory). Recently, there have appeared a number of publications tr ...
... Consider an arbitrary semifinite von Neumann algebra M and the algebra S(M) of all measurable operators affiliated with M (the algebra S(M) was first introduced by I.E. Segal in 1953 and is a cornerstone of noncommutative integration theory). Recently, there have appeared a number of publications tr ...