What Is Quantum Information? - Quantum Theory Group at CMU
... ◦ Present = perfectly present, Absent = perfectly absent ◦ There may be better ways of wording the theorem ...
... ◦ Present = perfectly present, Absent = perfectly absent ◦ There may be better ways of wording the theorem ...
Spin and Quantum Measurement
... The state of a quantum mechanical system is described mathematically by a normalized ket ψ that contains all the information we can know about the system. We have chosen the particular simplified schematic representation of SternGerlach experiments shown in Fig. 1.2 because it is the same representa ...
... The state of a quantum mechanical system is described mathematically by a normalized ket ψ that contains all the information we can know about the system. We have chosen the particular simplified schematic representation of SternGerlach experiments shown in Fig. 1.2 because it is the same representa ...
Shamsul Kaonain
... The "braket" notation is a very compact formalism for linear algebra which was introduced by Paul Dirac. It was introduced by Dirac in order to describe in a uniform manner vectors and linear operators both in the abstract Hilbert space 1 ...
... The "braket" notation is a very compact formalism for linear algebra which was introduced by Paul Dirac. It was introduced by Dirac in order to describe in a uniform manner vectors and linear operators both in the abstract Hilbert space 1 ...
QUANTUM PHASE ESTIMATION WITH ARBITRARY CONSTANT
... The Hadamard test outputs |0i or |1i with a fixed probability. We can model an iteration of Hadamard tests as Bernoulli trials with success probability (obtaining |1i) being pk . The best estimate for the probability of obtaining the post measurement state |1i with t samples is h ...
... The Hadamard test outputs |0i or |1i with a fixed probability. We can model an iteration of Hadamard tests as Bernoulli trials with success probability (obtaining |1i) being pk . The best estimate for the probability of obtaining the post measurement state |1i with t samples is h ...
2008
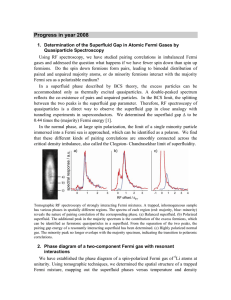
... Fermions are the fundamental building blocks of matter, whereas bosons emerge as composite particles. The simplest physical system to study the emergence of bosonic ...
... Fermions are the fundamental building blocks of matter, whereas bosons emerge as composite particles. The simplest physical system to study the emergence of bosonic ...
Symplectic Geometry and Geometric Quantization
... 1. Euclidean space: M = R2n with coordinates (q1 , ..., qn , p1 , ..., pn ), ω = d pi ∧ dqi . 2. Cotangent bundle : M = T ? N, where N is a manifold. M is the phase space of a system whose configuration space is N. M can be endowed with coordinates (qa , pb ), where at each point x = (q1 , ..., qn ) ...
... 1. Euclidean space: M = R2n with coordinates (q1 , ..., qn , p1 , ..., pn ), ω = d pi ∧ dqi . 2. Cotangent bundle : M = T ? N, where N is a manifold. M is the phase space of a system whose configuration space is N. M can be endowed with coordinates (qa , pb ), where at each point x = (q1 , ..., qn ) ...
Non-local quantum effects in cosmology 1
... generate temporal non-localities. There will be modifications to the FLRW (Friedmann, Lemaı̂tre, Robertson, Walker) equations governing the scale factor a(t), which in the classical theory are local differential equations. The effects of loops will generate new contributions where the equation for t ...
... generate temporal non-localities. There will be modifications to the FLRW (Friedmann, Lemaı̂tre, Robertson, Walker) equations governing the scale factor a(t), which in the classical theory are local differential equations. The effects of loops will generate new contributions where the equation for t ...
Symmetry and statistics
... √ (even for an infinitesimal non-diagonal element V ) |λi = (|+i + |−i)/ 2 is not a small perturbation of a supposed ground state |+i or |−i. In any quantum mechanical system with a finite number of degrees of freedom, tunnel effects give rise to non-diagonal elements connecting different ground sta ...
... √ (even for an infinitesimal non-diagonal element V ) |λi = (|+i + |−i)/ 2 is not a small perturbation of a supposed ground state |+i or |−i. In any quantum mechanical system with a finite number of degrees of freedom, tunnel effects give rise to non-diagonal elements connecting different ground sta ...
Why dynamics?
... 1. We are only beginning to understand the nature of quantum dynamics in some model systems: tip of the iceberg. 2. Many issues remain to settled: i) specific calculations a) dynamics of non-integrable systems b) correlation function and entanglement generation c) open systems: role of noise and dis ...
... 1. We are only beginning to understand the nature of quantum dynamics in some model systems: tip of the iceberg. 2. Many issues remain to settled: i) specific calculations a) dynamics of non-integrable systems b) correlation function and entanglement generation c) open systems: role of noise and dis ...
Relating Probability Amplitude Mechanics to
... When r is zero, there is no variability within the states, A, and everything the more detailed experiment measures is consistent with what the less detailed experiment had measured. In this case, Pr(Aj F ) = Pr(Aj C ), i.e., the detailed and less detailed experiment assign the same state probabiliti ...
... When r is zero, there is no variability within the states, A, and everything the more detailed experiment measures is consistent with what the less detailed experiment had measured. In this case, Pr(Aj F ) = Pr(Aj C ), i.e., the detailed and less detailed experiment assign the same state probabiliti ...
Coherent State Path Integrals
... that the number of bosons is a globally conserved quantity, which is why one is allowed to introduce a chemical potential, i.e. to use the Grand Canonical Ensemble in the first place. This formulation is useful to study superfluid Helium and similar problems. Suppose for instance that we want to com ...
... that the number of bosons is a globally conserved quantity, which is why one is allowed to introduce a chemical potential, i.e. to use the Grand Canonical Ensemble in the first place. This formulation is useful to study superfluid Helium and similar problems. Suppose for instance that we want to com ...
Quantum tomography via compressed sensing: error bounds, sample complexity and... estimators
... Recently, a new approach to tomography was proposed: compressed quantum tomography, based on techniques from compressed sensing [17, 18]. The basic idea is to concentrate on states that are well approximated by density matrices of rank r d. This approach can be applied to many realistic experiment ...
... Recently, a new approach to tomography was proposed: compressed quantum tomography, based on techniques from compressed sensing [17, 18]. The basic idea is to concentrate on states that are well approximated by density matrices of rank r d. This approach can be applied to many realistic experiment ...