Probability Relations between Separated Systems
... system by a suitable treatment of the second one. Since it has a finite chance of turning up, it will certainly turn up, if precisely the same experiments are repeated sufficiently often. Moreover, quite apart from special applications, the case that in the expansion (12) no coefficients vanish dese ...
... system by a suitable treatment of the second one. Since it has a finite chance of turning up, it will certainly turn up, if precisely the same experiments are repeated sufficiently often. Moreover, quite apart from special applications, the case that in the expansion (12) no coefficients vanish dese ...
pdf
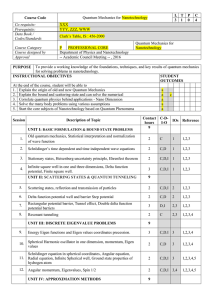
... 1. Explain the origin of old and new Quantum Mechanics a 2. Explain the bound and scattering state and can solve the numerical a c 3. Correlate quantum physics behind applications - Nano Dimension a 4. Solve the many body problems using various assumptions a 5. Start the core subjects of Nanotechnol ...
... 1. Explain the origin of old and new Quantum Mechanics a 2. Explain the bound and scattering state and can solve the numerical a c 3. Correlate quantum physics behind applications - Nano Dimension a 4. Solve the many body problems using various assumptions a 5. Start the core subjects of Nanotechnol ...
DIFFERENTIAL OPERATORS Math 21b, O. Knill
... transformations in infinite dimensions. The concept of a basis in infinite dimensions also needs to be defined properly. The linear map Df (x) = f ′ (x) can be iterated: Dn f = f (n) is the n’th derivative. It is a differential operator which allows to write differential equations like f ′′ − f ′ = ...
... transformations in infinite dimensions. The concept of a basis in infinite dimensions also needs to be defined properly. The linear map Df (x) = f ′ (x) can be iterated: Dn f = f (n) is the n’th derivative. It is a differential operator which allows to write differential equations like f ′′ − f ′ = ...
Transfer Matrices and Excitations with Matrix Product States
... Truncation of Virtual System Small D MPS can be understood as obtained from an RG procedure on on the virtual level → low energy representation ● RG network (e.g. MERA [5]) represents dominant eigenstate of ...
... Truncation of Virtual System Small D MPS can be understood as obtained from an RG procedure on on the virtual level → low energy representation ● RG network (e.g. MERA [5]) represents dominant eigenstate of ...
S. Mayboroda:
... The property of the localization of the eigenfunctions in rough domains or rough materials permeates acoustics, quantum physics, elasticity, to name just a few. Localization on fractal domains was used for noise abatement walls which up to date hold world efficiency record. Anderson localization of ...
... The property of the localization of the eigenfunctions in rough domains or rough materials permeates acoustics, quantum physics, elasticity, to name just a few. Localization on fractal domains was used for noise abatement walls which up to date hold world efficiency record. Anderson localization of ...
Topics in Quantum Information Theory
... Because the answers can now depend on what the interviewer is asking the other person. Alice and Bob can agree that they should give opposite answers if both are asked the S question and otherwise they should give the same answer. For many Alices and Bobs this gives < B >= 4 ≥ 2. Alice and Bob can h ...
... Because the answers can now depend on what the interviewer is asking the other person. Alice and Bob can agree that they should give opposite answers if both are asked the S question and otherwise they should give the same answer. For many Alices and Bobs this gives < B >= 4 ≥ 2. Alice and Bob can h ...
Aalborg Universitet The Landauer-Büttiker formula and resonant quantum transport
... dot levels across the fixed Fermi level of the system (recall that the latter is entirely controlled by the semi-infinite leads). Otherwise stated, the eigenvalues of H S (Vg ) equal the ones of H S (Vg = 0) (we denote them by {Ei }), up to a global shift Vg . Using the Landauer-Büttiker formula (8 ...
... dot levels across the fixed Fermi level of the system (recall that the latter is entirely controlled by the semi-infinite leads). Otherwise stated, the eigenvalues of H S (Vg ) equal the ones of H S (Vg = 0) (we denote them by {Ei }), up to a global shift Vg . Using the Landauer-Büttiker formula (8 ...
Credit Units:3
... continuous states, Infinite square-well potential (Particle in a rigid box problem): energy eigenvalues, eigenfunctions, momentum and position expectation values, zero-point energy, Scattering and bound state solutions of : (a) Step potential: reflectance and transmittance, probability current and i ...
... continuous states, Infinite square-well potential (Particle in a rigid box problem): energy eigenvalues, eigenfunctions, momentum and position expectation values, zero-point energy, Scattering and bound state solutions of : (a) Step potential: reflectance and transmittance, probability current and i ...
Axioms of Quantum Mechanics
... retrieve the value of a particular outcome, in a statistic manner. This separation of the experiment is reflected into the two types of mathematical objects we find in QM. The first step corresponds to the concept of a state of the system, while the second to observables. The state gives a complete des ...
... retrieve the value of a particular outcome, in a statistic manner. This separation of the experiment is reflected into the two types of mathematical objects we find in QM. The first step corresponds to the concept of a state of the system, while the second to observables. The state gives a complete des ...
QUANTUM DOTS
... First of all I do not know what is the Hubbard model, I have searched information about it in N. W. Ashcroft and N. D. Mermin, Solid State Physics,1976, Chap. 32, but I could not understand anything. Secondly I do not understand why they apply a particular unitary time evolution operator to the ini ...
... First of all I do not know what is the Hubbard model, I have searched information about it in N. W. Ashcroft and N. D. Mermin, Solid State Physics,1976, Chap. 32, but I could not understand anything. Secondly I do not understand why they apply a particular unitary time evolution operator to the ini ...
Properties of the Von Neumann entropy
... S(ρAB ) = 0 in the case of a bipartite pure state. That is, for the whole system the state is completely known, yet considering only one of the subsystems the measurement result could be complete random. This is the consequence of quantum entanglement. If we could somehow define a conditional Von Ne ...
... S(ρAB ) = 0 in the case of a bipartite pure state. That is, for the whole system the state is completely known, yet considering only one of the subsystems the measurement result could be complete random. This is the consequence of quantum entanglement. If we could somehow define a conditional Von Ne ...
1.1.3 (a) Prove that (AB)` = BAt using components
... (a) Prove or disprove in the case that M is a finite n x n matrix. (b) What if M is an infinite matrix? (Examples of infinite matrices are the representations of creation and destruction operators a and at in the quantum harmonic oscillator eigenstates {lo), 11) = atlo), 12) = a'll), ...1.) ...
... (a) Prove or disprove in the case that M is a finite n x n matrix. (b) What if M is an infinite matrix? (Examples of infinite matrices are the representations of creation and destruction operators a and at in the quantum harmonic oscillator eigenstates {lo), 11) = atlo), 12) = a'll), ...1.) ...
MASSACHUSETTS INSTITUTE OF TECHNOLOGY
... following problem are to be based on [ω = 1000, m = 1, x = 10, and kLR = 1] or [ω = 1000, m = 1, x = 1, kLR = 10]. The first set of parameters is close to the normal mode limit and the second set of parameters is close to the local mode limit. A. Set up the 11 × 11 P = 10 polyad. Solve for the energ ...
... following problem are to be based on [ω = 1000, m = 1, x = 10, and kLR = 1] or [ω = 1000, m = 1, x = 1, kLR = 10]. The first set of parameters is close to the normal mode limit and the second set of parameters is close to the local mode limit. A. Set up the 11 × 11 P = 10 polyad. Solve for the energ ...
Chapter 1 Review of Quantum Mechanics
... We have seen operators in QM behave just like matrices, such as transposed, Hermitian, and eigenvalue problems, etc. In fact, we can formulate a QM problem completely in terms of matrix analysis: a state becomes a column matrix and an operator becomes a square matrix. This is particularly useful if ...
... We have seen operators in QM behave just like matrices, such as transposed, Hermitian, and eigenvalue problems, etc. In fact, we can formulate a QM problem completely in terms of matrix analysis: a state becomes a column matrix and an operator becomes a square matrix. This is particularly useful if ...