1 An Approach to Geometry (stolen in part from Moise and Downs
... T5. Point Plotting Theorem Let AB be a ray, and let x be a positive number. Then there is exactly one point P of AB such that AP =x. Defn. A point B is called a midpoint of a segment AC if A-B-C and AB=BC. The midpoint of a segment is said to bisect the segment. Also, any line, plane, ray or segment ...
... T5. Point Plotting Theorem Let AB be a ray, and let x be a positive number. Then there is exactly one point P of AB such that AP =x. Defn. A point B is called a midpoint of a segment AC if A-B-C and AB=BC. The midpoint of a segment is said to bisect the segment. Also, any line, plane, ray or segment ...
My High School Math Note Book, Vol. 1
... It was easier, later, for me, to prepare for the tests, especially for the final exams at the end of the semester. I kept (and still do today) small notebooks where I collected not only mathematical but any idea I read in various domains. These two volumes reflect my 1973-1974 high school studies in ...
... It was easier, later, for me, to prepare for the tests, especially for the final exams at the end of the semester. I kept (and still do today) small notebooks where I collected not only mathematical but any idea I read in various domains. These two volumes reflect my 1973-1974 high school studies in ...
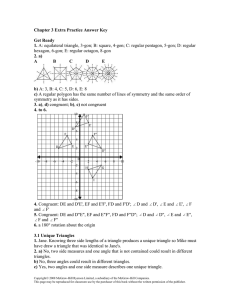
Answer
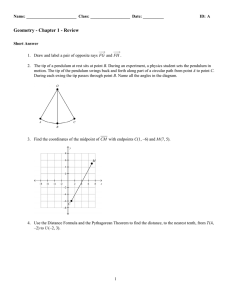
... on a coordinate plane contains Q(–2, 4) and R(4, –4). Add point T so that T is collinear with these points. Graph each point and draw ...
... on a coordinate plane contains Q(–2, 4) and R(4, –4). Add point T so that T is collinear with these points. Graph each point and draw ...
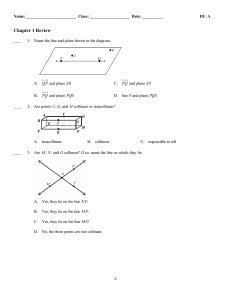
Unit 1 Review
... ____ 31. the point that divides a segment into two congruent segments ____ 32. to divide into two congruent parts ____ 33. a figure formed by two rays with a common endpoint ____ 34. the use of units to find a size or quantity ____ 35. a line, ray, or segment that divides a segment into two congruen ...
... ____ 31. the point that divides a segment into two congruent segments ____ 32. to divide into two congruent parts ____ 33. a figure formed by two rays with a common endpoint ____ 34. the use of units to find a size or quantity ____ 35. a line, ray, or segment that divides a segment into two congruen ...
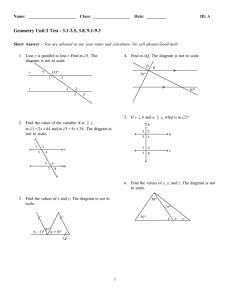
Unit 2 Practice Test w
... REF: 3-4 Parallel Lines and the Triangle Angle-Sum Theorem OBJ: 3-4.1 Finding Angle Measures in Triangles STA: CA GEOM 12.0| CA GEOM 13.0 KEY: triangle | sum of angles of a triangle | vertical angles ...
... REF: 3-4 Parallel Lines and the Triangle Angle-Sum Theorem OBJ: 3-4.1 Finding Angle Measures in Triangles STA: CA GEOM 12.0| CA GEOM 13.0 KEY: triangle | sum of angles of a triangle | vertical angles ...
Coterminal Angles and Trigonometric Ratios For Any
... The following diagram states the sign of the primary trigonometric ratios in all four quadrants. ...
... The following diagram states the sign of the primary trigonometric ratios in all four quadrants. ...
Geometry (H) Worksheet: 1st Semester Review:True/False, Always
... 40. Two lines perpendicular to the same line are parallel to each other. 41. Two lines parallel to the same line are parallel to each other. 42. Another name for an if-then statement is a conditional. 43. The converse of a conditional is formed by negating the hypothesis ad the conclusion. 44. The c ...
... 40. Two lines perpendicular to the same line are parallel to each other. 41. Two lines parallel to the same line are parallel to each other. 42. Another name for an if-then statement is a conditional. 43. The converse of a conditional is formed by negating the hypothesis ad the conclusion. 44. The c ...
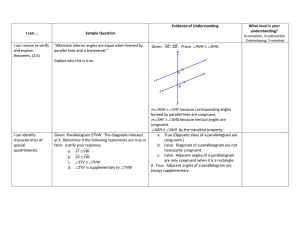
Prove Vertical Angles are Congruent. 2 1 34° 2x + 16 124° 3x + 16
... each conclusion. This process is often difficult for new geometry students – it is hard to clearly explain what you know and why you know it. One format for a proof is to provide it in a paragraph form. To simply write it as you would say it. This can be a comfortable style for many students. The ke ...
... each conclusion. This process is often difficult for new geometry students – it is hard to clearly explain what you know and why you know it. One format for a proof is to provide it in a paragraph form. To simply write it as you would say it. This can be a comfortable style for many students. The ke ...