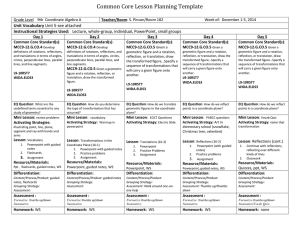
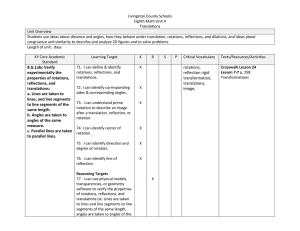
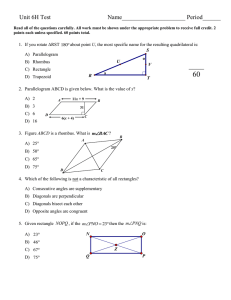
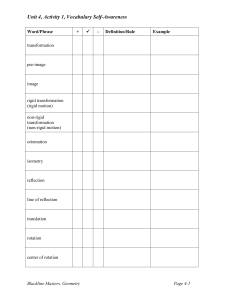
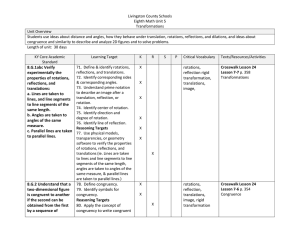
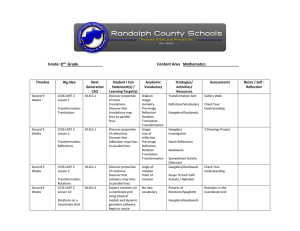
1.1 Angles
... Ray. If we drop the part of the line AB that lies “before” the point A, what remains is called ray AB. Thus, ray AB is the portion of the line AB that starts at A, continues through B, and on past B to infinity. Here, point A is called the endpoint of ray AB. We will now use the concept of a ray to ...
... Ray. If we drop the part of the line AB that lies “before” the point A, what remains is called ray AB. Thus, ray AB is the portion of the line AB that starts at A, continues through B, and on past B to infinity. Here, point A is called the endpoint of ray AB. We will now use the concept of a ray to ...
Geometric Transformations Sequence
... represent rotations. For example, a rotation by 90o about the origin is simply multiplication by the imaginary unit i. If complex numbers are known to students in more advanced levels using polar form, the rotation of an object through angle φ around the origin can be represented by multiplicat ...
... represent rotations. For example, a rotation by 90o about the origin is simply multiplication by the imaginary unit i. If complex numbers are known to students in more advanced levels using polar form, the rotation of an object through angle φ around the origin can be represented by multiplicat ...
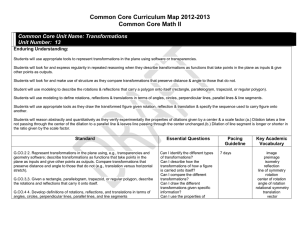
Unit 7: Transformations in the Coordinate Plane
... At the end of Unit student’s should be able to say “I can…” describe and compare function transformations on a set of points as inputs to produce another set of points as outputs, including translations and horizontal or vertical stretching represent and compare rigid and size transformations of ...
... At the end of Unit student’s should be able to say “I can…” describe and compare function transformations on a set of points as inputs to produce another set of points as outputs, including translations and horizontal or vertical stretching represent and compare rigid and size transformations of ...
CMSC 425: Lecture 6 Affine Transformations and Rotations
... about which the reflection is performed is one of the coordinate planes (corresponding to x = 0, y = 0, or z = 0). For example, to reflect points about the yz-coordinate plane (that is, the plane x = 0), we can scale the x-coordinate by −1 (see Fig. 3(c)). Using the scaling matrix above, we have the ...
... about which the reflection is performed is one of the coordinate planes (corresponding to x = 0, y = 0, or z = 0). For example, to reflect points about the yz-coordinate plane (that is, the plane x = 0), we can scale the x-coordinate by −1 (see Fig. 3(c)). Using the scaling matrix above, we have the ...