chapterS4BuildingBlo..
... • How do quantum laws prevent electrons from collapsing into the nucleus allowing atoms to be stable for more than 10-23 seconds? – Uncertainty in position near the nucleus allows for uncertainty in momentum near the nucleus, so momentum can not become zero. ...
... • How do quantum laws prevent electrons from collapsing into the nucleus allowing atoms to be stable for more than 10-23 seconds? – Uncertainty in position near the nucleus allows for uncertainty in momentum near the nucleus, so momentum can not become zero. ...
chapterS4BuildingBlo..
... Degeneracy Pressure in Stars • Electron degeneracy pressure is what supports white dwarfs against gravity—quantum laws prevent its electrons from being squeezed into a smaller space I* • Neutron degeneracy pressure is what supports neutron stars against gravity—quantum laws prevent its neutrons fro ...
... Degeneracy Pressure in Stars • Electron degeneracy pressure is what supports white dwarfs against gravity—quantum laws prevent its electrons from being squeezed into a smaller space I* • Neutron degeneracy pressure is what supports neutron stars against gravity—quantum laws prevent its neutrons fro ...
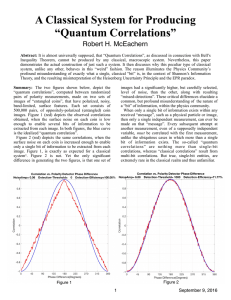
Quantum Correlations
... More generally, this “single bit of information” phenomenon, is at the heart of the correct interpretation of the Heisenberg Uncertainty Principle, of which the EPR paradox 4 and Bell’s Theorem are merely special cases. The uncertainty principle, in turn, is merely the special case of Shannon’s Capa ...
... More generally, this “single bit of information” phenomenon, is at the heart of the correct interpretation of the Heisenberg Uncertainty Principle, of which the EPR paradox 4 and Bell’s Theorem are merely special cases. The uncertainty principle, in turn, is merely the special case of Shannon’s Capa ...
Quantum phase transitions and novel phases in condensed matter
... Phase diagrams of LiHoF4 and a typical high-Tc superconductor such as YBa2Cu3O6+x ...
... Phase diagrams of LiHoF4 and a typical high-Tc superconductor such as YBa2Cu3O6+x ...
FullText
... Previously we have shown the CL emission spectrum for this materials collected in the STEM-CL[6]. Due to the high beam current in a very small area it is not possible to hold the beam on a single DR and collect a CL emission spectrum. The observed 622 nm emission peak has a full width at half heigh ...
... Previously we have shown the CL emission spectrum for this materials collected in the STEM-CL[6]. Due to the high beam current in a very small area it is not possible to hold the beam on a single DR and collect a CL emission spectrum. The observed 622 nm emission peak has a full width at half heigh ...
Powerpoint 8/12
... We have only discussed two types of errors, bit flips and phase flips. What about “general” errors? Theorem of digitizing quantum errors: If we can correct errors in some set, then we can correct any linear complex combination of such errors. ...
... We have only discussed two types of errors, bit flips and phase flips. What about “general” errors? Theorem of digitizing quantum errors: If we can correct errors in some set, then we can correct any linear complex combination of such errors. ...
Press Release How atoms change places Physicists from the
... lattice sites in which the dynamics of a few interacting atoms can be studied in detail. „In these double wells, we were able to directly observe how two neighboring atoms with different spins change places” says Trotzky. The spin of a particle can be understood as an internal rotation and forms the ...
... lattice sites in which the dynamics of a few interacting atoms can be studied in detail. „In these double wells, we were able to directly observe how two neighboring atoms with different spins change places” says Trotzky. The spin of a particle can be understood as an internal rotation and forms the ...
Quantum cryptography
... Alice and Bob agree on a random permutation of the bits in the key They split the key into blocks of length k Compare the parity of each block. If they compute the same parity, the block is considered correct. If their parity is different, they look for the erroneous bit, using a binary search in th ...
... Alice and Bob agree on a random permutation of the bits in the key They split the key into blocks of length k Compare the parity of each block. If they compute the same parity, the block is considered correct. If their parity is different, they look for the erroneous bit, using a binary search in th ...
The Theory of Everything
... atomic conformations of small molecules, simple chemical reaction rates, structural phase transitions, ferromagnetism, and sometimes even superconducting transition temperatures (7). But the schemes for approximating are not first-principles deductions but are rather art keyed to experiment, and thu ...
... atomic conformations of small molecules, simple chemical reaction rates, structural phase transitions, ferromagnetism, and sometimes even superconducting transition temperatures (7). But the schemes for approximating are not first-principles deductions but are rather art keyed to experiment, and thu ...
Quantum Gravity www.AssignmentPoint.com Quantum gravity (QG
... obvious way of combining the two (such as treating gravity as simply another particle field) ran quickly into what is known as the renormalization problem. In the old-fashioned understanding of renormalization, gravity particles would attract each other and adding together all of the interactions r ...
... obvious way of combining the two (such as treating gravity as simply another particle field) ran quickly into what is known as the renormalization problem. In the old-fashioned understanding of renormalization, gravity particles would attract each other and adding together all of the interactions r ...
slides - Frontiers of Fundamental Physics (FFP14)
... “Einstein’s later critiques of quantum theory focused less on its indeterminacy and more on its strange epistemological status. In quantum mechanics the actual act of measurement is part of the theory; these magic coins just mentioned exist in a state of (heads, tails)-(tails, heads) uncertainty unt ...
... “Einstein’s later critiques of quantum theory focused less on its indeterminacy and more on its strange epistemological status. In quantum mechanics the actual act of measurement is part of the theory; these magic coins just mentioned exist in a state of (heads, tails)-(tails, heads) uncertainty unt ...
LanZ_0112_eps(1).
... even nanoparticles, to decelerate a hot fast gas beam to zero velocity by using an optical cavity. This deceleration method is based on a novel phase stability mechanism in the bad cavity regime, which is very different from the traditional cavity cooling studies where a good cavity is needed. We pr ...
... even nanoparticles, to decelerate a hot fast gas beam to zero velocity by using an optical cavity. This deceleration method is based on a novel phase stability mechanism in the bad cavity regime, which is very different from the traditional cavity cooling studies where a good cavity is needed. We pr ...
Network Tomography
... Computational cost per time step should be bounded by constant independent of time ...
... Computational cost per time step should be bounded by constant independent of time ...
PDF
... The spin is a intrinsic symmetry property, or quantum observable of all quantum particles, and its orientation is an important degree of freedom. Roughly speaking, the spin of a particle is a contribution to its angular momentum that is not due to its motion but whose correct calculation requires re ...
... The spin is a intrinsic symmetry property, or quantum observable of all quantum particles, and its orientation is an important degree of freedom. Roughly speaking, the spin of a particle is a contribution to its angular momentum that is not due to its motion but whose correct calculation requires re ...
Glueballs
... • A meson in SU(2) will have I=1, so Iz=+1,0,-1. Three pions were found: π+, π0,π• If we take two particles with isospin up or down: 1:↑↓ 2:↑↓ they can combine as follows ↑↑ with Iz=+1, ↓↓ with Iz=-1 and two possible linear combinations of ↑↓, ↓↑ with both Iz=0 ...
... • A meson in SU(2) will have I=1, so Iz=+1,0,-1. Three pions were found: π+, π0,π• If we take two particles with isospin up or down: 1:↑↓ 2:↑↓ they can combine as follows ↑↑ with Iz=+1, ↓↓ with Iz=-1 and two possible linear combinations of ↑↓, ↓↑ with both Iz=0 ...
What is Time in Quantum Mechanics?
... destroy objects. Quantum mechanics, therefore, must include irreversibility. Quoting from Ilya Prigogine [27]: “I believe that we are at an important turning point in the history of science. We have come to the end of the road paved by Galileo and Newton, which presented us with an image of time–rev ...
... destroy objects. Quantum mechanics, therefore, must include irreversibility. Quoting from Ilya Prigogine [27]: “I believe that we are at an important turning point in the history of science. We have come to the end of the road paved by Galileo and Newton, which presented us with an image of time–rev ...
What is quantum chaos?
... In the semiclassical limit the spectral properties of classically chaotic Hamiltonian are universally described by random matrix theory. With the help of the one parameter scaling theory we propose an alternative characterization of this universality class. It is also identified the universality cla ...
... In the semiclassical limit the spectral properties of classically chaotic Hamiltonian are universally described by random matrix theory. With the help of the one parameter scaling theory we propose an alternative characterization of this universality class. It is also identified the universality cla ...
Chapter 2 Statistical Thermodynamics 1
... a particle of the system. But quantum particles may have spin as well. Thus we must multiply the above equation by a spin factor γs: g ( )d s ...
... a particle of the system. But quantum particles may have spin as well. Thus we must multiply the above equation by a spin factor γs: g ( )d s ...
Were Bohr and Einstein both right
... (bosons being generated by these) which are known to define physics at the fundamental level. ...
... (bosons being generated by these) which are known to define physics at the fundamental level. ...
A COURSE IN QUANTUM PHYSICS AND RELATIVITY FOR
... Class participants who have questions outside of class are encouraged to send me an email. If you need a quick answer or if the nature of your question is not suited to email format, you may contact me via phone. If I can’t talk when you call, I will get back to you as soon as possible, but always w ...
... Class participants who have questions outside of class are encouraged to send me an email. If you need a quick answer or if the nature of your question is not suited to email format, you may contact me via phone. If I can’t talk when you call, I will get back to you as soon as possible, but always w ...
Gravity and Quantum Mechanics
... • Experimental confirmation of Maxwell’s term took 25 years (Hertz 1886). In order to do this, he had to open and close the switch on the nanosecond time scale, a challenging feat in the 1800’s. • In order to probe quantum gravity, we need to reach the nano-nano-nano-nano-nano second time scale (th ...
... • Experimental confirmation of Maxwell’s term took 25 years (Hertz 1886). In order to do this, he had to open and close the switch on the nanosecond time scale, a challenging feat in the 1800’s. • In order to probe quantum gravity, we need to reach the nano-nano-nano-nano-nano second time scale (th ...
PDF
... Instead of looking at the Turing machine model (a model of variable-length computation) let us look at the Boolean circuit model (a model of fixedlength computation). The reason for choosing the Boolean circuit model to compare with quantum theory is that in quantum theory, we need to work in a stat ...
... Instead of looking at the Turing machine model (a model of variable-length computation) let us look at the Boolean circuit model (a model of fixedlength computation). The reason for choosing the Boolean circuit model to compare with quantum theory is that in quantum theory, we need to work in a stat ...
Talk, 15 MB - Seth Aubin - College of William and Mary
... Surprise! Reach Tc with only a 30x loss in number. (trap loaded with 2x107 atoms) Experimental cycle = 5 - 15 seconds ...
... Surprise! Reach Tc with only a 30x loss in number. (trap loaded with 2x107 atoms) Experimental cycle = 5 - 15 seconds ...
Quantum Gravity - General overview and recent developments
... Perturbation theory proabably finite at all orders, but sum diverges ...
... Perturbation theory proabably finite at all orders, but sum diverges ...
Planck-scale Metaphysics
... “If one assigns the intrinsic 3-geometry, one cannot also specify the extrinsic curvature. The uncertainty principle thus deprives one of any way whatsoever to predict, or even give meaning to, 'the deterministic classical history of space evolving in time'.” (C.W. Misner, K.S. Thorne, J.A. Wheeler ...
... “If one assigns the intrinsic 3-geometry, one cannot also specify the extrinsic curvature. The uncertainty principle thus deprives one of any way whatsoever to predict, or even give meaning to, 'the deterministic classical history of space evolving in time'.” (C.W. Misner, K.S. Thorne, J.A. Wheeler ...
Quantum tomography
Quantum tomography or quantum state tomography is the process of reconstructing the quantum state (density matrix) for a source of quantum systems by measurements on the systems coming from the source. The source may be any device or system which prepares quantum states either consistently into quantum pure states or otherwise into general mixed states. To be able to uniquely identify the state, the measurements must be tomographically complete. That is, the measured operators must form an operator basis on the Hilbert space of the system, providing all the information about the state. Such a set of observations is sometimes called a quorum. In quantum process tomography on the other hand, known quantum states are used to probe a quantum process to find out how the process can be described. Similarly, quantum measurement tomography works to find out what measurement is being performed.The general principle behind quantum state tomography is that by repeatedly performing many different measurements on quantum systems described by identical density matrices, frequency counts can be used to infer probabilities, and these probabilities are combined with Born's rule to determine a density matrix which fits the best with the observations.This can be easily understood by making a classical analogy. Let us consider a harmonic oscillator (e.g. a pendulum). The position and momentum of the oscillator at any given point can be measured and therefore the motion can be completely described by the phase space. This is shown in figure 1. By performing this measurement for a large number of identical oscillators we get a possibility distribution in the phase space (figure 2). This distribution can be normalized (the oscillator at a given time has to be somewhere) and the distribution must be non-negative. So we have retrieved a function W(x,p) which gives a description of the chance of finding the particle at a given point with a given momentum. For quantum mechanical particles the same can be done. The only difference is that the Heisenberg’s uncertainty principle mustn’t be violated, meaning that we cannot measure the particle’s momentum and position at the same time. The particle’s momentum and its position are called quadratures (see Optical phase space for more information) in quantum related states. By measuring one of the quadratures of a large number of identical quantum states will give us a probability density corresponding to that particular quadrature. This is called the marginal distribution, pr(X) or pr(P) (see figure 3). In the following text we will see that this probability density is needed to characterize the particle’s quantum state, which is the whole point of quantum tomography.