Lecture IX - Functorial Property of the Fundamental Group
... Lecture IX - Functorial Property of the Fundamental Group We now turn to the most basic functor in algebraic topology namely, the π1 functor. Recall that the fundamental group of a space involves a base point and according to theorem (7.8) the fundamental group of a path connected space is unique up ...
... Lecture IX - Functorial Property of the Fundamental Group We now turn to the most basic functor in algebraic topology namely, the π1 functor. Recall that the fundamental group of a space involves a base point and according to theorem (7.8) the fundamental group of a path connected space is unique up ...
Sandwich-type characterization of completely regular spaces
... The concept of a compact-like function shows that sandwich-type characterizations of higher separation axioms, viz.: perfect normality [9], complete normality [7], normality ([6] and [10]), continue to hold for the case of complete regularity. We shall need the following general insertion theorem. T ...
... The concept of a compact-like function shows that sandwich-type characterizations of higher separation axioms, viz.: perfect normality [9], complete normality [7], normality ([6] and [10]), continue to hold for the case of complete regularity. We shall need the following general insertion theorem. T ...
CONCERNING SEMI-CONTINUOUS FUNCTIONS Dragan S
... Finally, the fact that continuity implies weak-continuity gives that the Theorem A is the consequence of Corollary 2. ...
... Finally, the fact that continuity implies weak-continuity gives that the Theorem A is the consequence of Corollary 2. ...
MA4266_Lect10
... Properties of Compact Sets Theorem 6.5: If A and B are disjoint compact subsets of a Hausdorff space X then there exist disjoint open subsets U and V of X with A U , B V . Proof Similar to the proof of theorem 6.4. Question Construct an example of a compact subset of a topological space Hint: ...
... Properties of Compact Sets Theorem 6.5: If A and B are disjoint compact subsets of a Hausdorff space X then there exist disjoint open subsets U and V of X with A U , B V . Proof Similar to the proof of theorem 6.4. Question Construct an example of a compact subset of a topological space Hint: ...
For the Oral Candidacy examination, the student is examined in
... For the Oral Candidacy examination, the student is examined in three basic subjects (satisfying the requirements of the student's intended Track of Specialization). For each subject, the student must master all of the topics listed on the syllabus. The student is expected to have a through understan ...
... For the Oral Candidacy examination, the student is examined in three basic subjects (satisfying the requirements of the student's intended Track of Specialization). For each subject, the student must master all of the topics listed on the syllabus. The student is expected to have a through understan ...
Free full version - topo.auburn.edu
... in X∞ . Let Xi = X∞ /Fi be the space obtained by collapsing the closed set Fi to a point. Then Xi is a one-point compactification of Ui and hence homeomorphic to the n-sphere S n . Since the sequence (Fi ) is decreasing, there are natural maps pji : Xj → Xi for j > i, and we get an inverse sequence ...
... in X∞ . Let Xi = X∞ /Fi be the space obtained by collapsing the closed set Fi to a point. Then Xi is a one-point compactification of Ui and hence homeomorphic to the n-sphere S n . Since the sequence (Fi ) is decreasing, there are natural maps pji : Xj → Xi for j > i, and we get an inverse sequence ...
MAT 371 Advanced Calculus Introductory topology references
... The definitions and theorems from elementary topology stated here are meant to give a higher level unifying view of items covered in the MAT 371 textbook, and to invite students to study more topology in MAT 410. Definition. A topological space is a set X together with a collection T of subsets of X ...
... The definitions and theorems from elementary topology stated here are meant to give a higher level unifying view of items covered in the MAT 371 textbook, and to invite students to study more topology in MAT 410. Definition. A topological space is a set X together with a collection T of subsets of X ...
On the Identity Component of Topological Groups
... Go of G, in general, is not open, some algebraic condition imposed on Go may happen to ensure that Go to be open. One of these conditions will be found in Theorem 1, and it will be shown that such groups are a-compact. In order to prove the a-compactness, we need the following known theorem; A local ...
... Go of G, in general, is not open, some algebraic condition imposed on Go may happen to ensure that Go to be open. One of these conditions will be found in Theorem 1, and it will be shown that such groups are a-compact. In order to prove the a-compactness, we need the following known theorem; A local ...
HOMEOMORPHISM IN IDEL TOPOLOGICAL SPACES Author: N.CHANDRAMATHI , K. BHUVANESWARI S.BHARATHI, INDIA
... (i) Semi open if A ⊆cl (int (A)) and semi closed if int(cl (A))⊆A. (ii) Pre-open if A ⊆ int (cl (A)) and pre-closed if cl (int (A))⊆ A. Definition 1.2: A subset A of a space (X,τ )is called ω-closed[9] if cl(A)⊆U whenever A⊆U and U is semi open in X. Definition 1.3:A map f:(X,τ )→(Y,σ) is said to be ...
... (i) Semi open if A ⊆cl (int (A)) and semi closed if int(cl (A))⊆A. (ii) Pre-open if A ⊆ int (cl (A)) and pre-closed if cl (int (A))⊆ A. Definition 1.2: A subset A of a space (X,τ )is called ω-closed[9] if cl(A)⊆U whenever A⊆U and U is semi open in X. Definition 1.3:A map f:(X,τ )→(Y,σ) is said to be ...
Modern index theory CIRM
... This index depends only on the symbol of D. The Atiyah-Singer index theorem expresses this index by means of a topological expression in terms of this symbol. Using a Chern character and applied to special operators coming from geometry, there is a very explicit cohomological formula for this index. ...
... This index depends only on the symbol of D. The Atiyah-Singer index theorem expresses this index by means of a topological expression in terms of this symbol. Using a Chern character and applied to special operators coming from geometry, there is a very explicit cohomological formula for this index. ...
compact - Maths, NUS
... Properties of Compact Sets Theorem 6.5: If A and B are disjoint compact subsets of a Hausdorff space X then there exist disjoint open subsets U and V of X with A U , B V . Proof Similar to the proof of theorem 6.4. Question Construct an example of a compact subset of a topological space Hint: ...
... Properties of Compact Sets Theorem 6.5: If A and B are disjoint compact subsets of a Hausdorff space X then there exist disjoint open subsets U and V of X with A U , B V . Proof Similar to the proof of theorem 6.4. Question Construct an example of a compact subset of a topological space Hint: ...
Weak-continuity and closed graphs
... WEAK-CONTINUITY AND CLOSED GRAPHS TAKASHI NOIRI, Yatsushiro ...
... WEAK-CONTINUITY AND CLOSED GRAPHS TAKASHI NOIRI, Yatsushiro ...
COMPACT SÍ-SOUSLIN SETS ARE Ga`S result holds for f
... [7]), mostly in the direction of abstractions of Halmos' proof. For example, every Baire set is "distinguishable" and every compact distinguishable set is a
... [7]), mostly in the direction of abstractions of Halmos' proof. For example, every Baire set is "distinguishable" and every compact distinguishable set is a
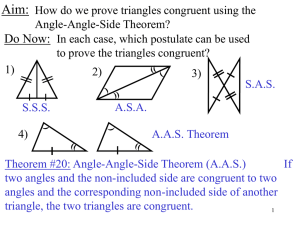
AAS Theorem - Math Story
... Theorem #20: Angle-Angle-Side Theorem (A.A.S.) If two angles and the non-included side are congruent to two angles and the corresponding non-included side of another triangle, the two triangles are congruent. ...
... Theorem #20: Angle-Angle-Side Theorem (A.A.S.) If two angles and the non-included side are congruent to two angles and the corresponding non-included side of another triangle, the two triangles are congruent. ...
File
... OBJECTIVE: I will will draw valid conclusions and will prove angles congruent using congruent complement and supplement theorems. ...
... OBJECTIVE: I will will draw valid conclusions and will prove angles congruent using congruent complement and supplement theorems. ...
USC3002 Picturing the World Through Mathematics
... every finite collection of sets in C is nonempty) and the intersection of all the sets in C is empty. From these two properties we can find a sequence C j in with ...
... every finite collection of sets in C is nonempty) and the intersection of all the sets in C is empty. From these two properties we can find a sequence C j in with ...
MA4266_Lect17
... every finite collection of sets in C is nonempty) and the intersection of all the sets in C is empty. From these two properties we can find a sequence C j in with ...
... every finite collection of sets in C is nonempty) and the intersection of all the sets in C is empty. From these two properties we can find a sequence C j in with ...
USC3002 Picturing the World Through Mathematics
... Hausdorff spaces is a Hausdorff space. Theorem 7.3 The product of a finite number of connected spaces is a connected space. Theorem 7.4 The product of a finite number of separable spaces is separable. Theorem 7.5 The product of a finite number of 1st (2nd) countable spaces is 1st (2nd) countable. Th ...
... Hausdorff spaces is a Hausdorff space. Theorem 7.3 The product of a finite number of connected spaces is a connected space. Theorem 7.4 The product of a finite number of separable spaces is separable. Theorem 7.5 The product of a finite number of 1st (2nd) countable spaces is 1st (2nd) countable. Th ...
MA4266_Lect13
... Hausdorff spaces is a Hausdorff space. Theorem 7.3 The product of a finite number of connected spaces is a connected space. Theorem 7.4 The product of a finite number of separable spaces is separable. Theorem 7.5 The product of a finite number of 1st (2nd) countable spaces is 1st (2nd) countable. Th ...
... Hausdorff spaces is a Hausdorff space. Theorem 7.3 The product of a finite number of connected spaces is a connected space. Theorem 7.4 The product of a finite number of separable spaces is separable. Theorem 7.5 The product of a finite number of 1st (2nd) countable spaces is 1st (2nd) countable. Th ...
Pizzas, Bagels, Pretzels, and Euler`s Magical χ
... If the second axiom, that of idempotence, is relaxed, then the axioms define a preclosure operator. ...
... If the second axiom, that of idempotence, is relaxed, then the axioms define a preclosure operator. ...
Configurations of points - University of Edinburgh
... In this paper I will discuss a problem in elementary geometry that has arisen from the investigations of Berry & Robbins (1997) on the spin-statistics theorem of quantum mechanics. The question concerns n distinct particles in Euclidean 3-space, idealized as points, and it aims to bridge the gap to ...
... In this paper I will discuss a problem in elementary geometry that has arisen from the investigations of Berry & Robbins (1997) on the spin-statistics theorem of quantum mechanics. The question concerns n distinct particles in Euclidean 3-space, idealized as points, and it aims to bridge the gap to ...
LECTURE 30: INDUCED MAPS BETWEEN CLASSIFYING SPACES
... by providing a natural transformation between the functors that these spaces rep resent: α∗ : {Gbundles over X} → {Hbundles over X}. Namely, send a Gbundle E → X to the Hbundle H ×G E → X where G acts on H through the homomorphism α. Thus B may be viewed as a functor Topological groups → homoto ...
... by providing a natural transformation between the functors that these spaces rep resent: α∗ : {Gbundles over X} → {Hbundles over X}. Namely, send a Gbundle E → X to the Hbundle H ×G E → X where G acts on H through the homomorphism α. Thus B may be viewed as a functor Topological groups → homoto ...
Introduction to Index Theory Notes
... One can always choose such a P (see original Atiyah-Singer papers in the Annals). The analytic index a − ind : K 0 (B ∗ X, S ∗ X) → Z is defined to be h i f , α 7→ dim ker P − dim ker P ∗ . Ve , W Theorem 4.1. (Atiyah-Singer Index Theorem) We have a − ind = t − ind. This may be translated as an inte ...
... One can always choose such a P (see original Atiyah-Singer papers in the Annals). The analytic index a − ind : K 0 (B ∗ X, S ∗ X) → Z is defined to be h i f , α 7→ dim ker P − dim ker P ∗ . Ve , W Theorem 4.1. (Atiyah-Singer Index Theorem) We have a − ind = t − ind. This may be translated as an inte ...
Michael Atiyah

Sir Michael Francis Atiyah, OM, FRS, FRSE, FMedSci FAA, HonFREng (born 22 April 1929) is a British mathematician specialising in geometry.Atiyah grew up in Sudan and Egypt and spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study. He has been president of the Royal Society (1990–1995), master of Trinity College, Cambridge (1990–1997), chancellor of the University of Leicester (1995–2005), and president of the Royal Society of Edinburgh (2005–2008). Since 1997, he has been an honorary professor at the University of Edinburgh.Atiyah's mathematical collaborators include Raoul Bott, Friedrich Hirzebruch and Isadore Singer, and his students include Graeme Segal, Nigel Hitchin and Simon Donaldson. Together with Hirzebruch, he laid the foundations for topological K-theory, an important tool in algebraic topology, which, informally speaking, describes ways in which spaces can be twisted. His best known result, the Atiyah–Singer index theorem, was proved with Singer in 1963 and is widely used in counting the number of independent solutions to differential equations. Some of his more recent work was inspired by theoretical physics, in particular instantons and monopoles, which are responsible for some subtle corrections in quantum field theory. He was awarded the Fields Medal in 1966, the Copley Medal in 1988, and the Abel Prize in 2004.