Chapter 10 Solids & Liquids continued
... FB = ρ Water gVWater (displaced) = ρ Water g( ARaft h) ...
... FB = ρ Water gVWater (displaced) = ρ Water g( ARaft h) ...
rate of change
... The Lagrangian term dt is the rate of change experienced by a given tagged water parcel. The Eulerian term t is the local rate of change at a fixed point. du ...
... The Lagrangian term dt is the rate of change experienced by a given tagged water parcel. The Eulerian term t is the local rate of change at a fixed point. du ...
Lecture01 - Lcgui.net
... - Read textbook 1.1-1.2 on page 3-5 -Questions and Problems: 1 and 2 on page 17 1. Provide definitions for the following measureable flow properties: angular momentum, entropy, thermal conductivity, molecular diffusivity, and surface tension. 2. List the established names for the SI units of force, ...
... - Read textbook 1.1-1.2 on page 3-5 -Questions and Problems: 1 and 2 on page 17 1. Provide definitions for the following measureable flow properties: angular momentum, entropy, thermal conductivity, molecular diffusivity, and surface tension. 2. List the established names for the SI units of force, ...
Phy 211: General Physics I
... If the surface of a fluid is exposed to air, the pressure at that surface (Po) is equal to that of the atmospheric air pressure at that elevation, this is a consequence of Pascal’s Principle. At sea level the atmospheric pressure is ...
... If the surface of a fluid is exposed to air, the pressure at that surface (Po) is equal to that of the atmospheric air pressure at that elevation, this is a consequence of Pascal’s Principle. At sea level the atmospheric pressure is ...
Lecture01 - Lcgui.net
... - Read textbook 1.1-1.2 on page 3-5 -Questions and Problems: 1 and 2 on page 17 1. Provide definitions for the following measureable flow properties: angular momentum, entropy, thermal conductivity, molecular diffusivity, and surface tension. 2. List the established names for the SI units of force, ...
... - Read textbook 1.1-1.2 on page 3-5 -Questions and Problems: 1 and 2 on page 17 1. Provide definitions for the following measureable flow properties: angular momentum, entropy, thermal conductivity, molecular diffusivity, and surface tension. 2. List the established names for the SI units of force, ...
Fluids in Motion
... Example 3: Water flowing at 4 m/s passes through a Venturi tube as shown. If h = 12 cm, what is the velocity of the water in the constriction? Bernoulli’s Equation (h1 = h2) ...
... Example 3: Water flowing at 4 m/s passes through a Venturi tube as shown. If h = 12 cm, what is the velocity of the water in the constriction? Bernoulli’s Equation (h1 = h2) ...
The Material Derivative The equations above apply to a fluid
... Newton’s laws of motion and therefore the Navier-Stokes equation apply only in an inertial frame of reference. When considering the flow of rotating bodies such as the Earth (or other rotating bodies such as the sun or galaxies), it is convenient to choose coordinate axes which rotate with the body ...
... Newton’s laws of motion and therefore the Navier-Stokes equation apply only in an inertial frame of reference. When considering the flow of rotating bodies such as the Earth (or other rotating bodies such as the sun or galaxies), it is convenient to choose coordinate axes which rotate with the body ...
Full-text
... bodies. Word “interaction” basically means forces and moments acting on body in fluid flow. Also, important is question about pressure distribution on body surface. It’s hard to solve such problems in analytic manners, so the only way to get correct and practically useful results is to do experiment ...
... bodies. Word “interaction” basically means forces and moments acting on body in fluid flow. Also, important is question about pressure distribution on body surface. It’s hard to solve such problems in analytic manners, so the only way to get correct and practically useful results is to do experiment ...
Chapter 14
... • Steady (laminar) – the velocity of the moving fluid at any fixed point does not change with time (either in magnitude or direction) • Incompressible – density is constant and uniform • Nonviscous – the fluid experiences no drag force • Irrotational – in this flow the test body will not rotate abou ...
... • Steady (laminar) – the velocity of the moving fluid at any fixed point does not change with time (either in magnitude or direction) • Incompressible – density is constant and uniform • Nonviscous – the fluid experiences no drag force • Irrotational – in this flow the test body will not rotate abou ...
Chapter 9
... cm/s. The average flow speed of the air doubles through a constriction in the bronchus. Assuming incompressible flow, determine the pressure drop in the constriction. ...
... cm/s. The average flow speed of the air doubles through a constriction in the bronchus. Assuming incompressible flow, determine the pressure drop in the constriction. ...
Chapter 14
... • Steady (laminar) – the velocity of the moving fluid at any fixed point does not change with time (either in magnitude or direction) • Incompressible – density is constant and uniform • Nonviscous – the fluid experiences no drag force • Irrotational – in this flow the test body will not rotate abou ...
... • Steady (laminar) – the velocity of the moving fluid at any fixed point does not change with time (either in magnitude or direction) • Incompressible – density is constant and uniform • Nonviscous – the fluid experiences no drag force • Irrotational – in this flow the test body will not rotate abou ...
A Brief History of Planetary Science
... slow moving fluids This is known as Bernoulli’s principle Based on conservation of energy ...
... slow moving fluids This is known as Bernoulli’s principle Based on conservation of energy ...
Fluid Dynamics - AP Physics B, Mr. B's Physics Planet Home
... Up till now, we have pretty much focused on fluids at rest. Now let's look at fluids in motion It is important that you understand that an IDEAL FLUID: ...
... Up till now, we have pretty much focused on fluids at rest. Now let's look at fluids in motion It is important that you understand that an IDEAL FLUID: ...
AP_Physics_B_-_Fluid_Dynamics
... Up till now, we have pretty much focused on fluids at rest. Now let's look at fluids in motion It is important that you understand that an IDEAL FLUID: • Is non viscous (meaning there is NO internal friction) • Is incompressible (meaning its Density is constant) • Its motion is steady and NON – TURB ...
... Up till now, we have pretty much focused on fluids at rest. Now let's look at fluids in motion It is important that you understand that an IDEAL FLUID: • Is non viscous (meaning there is NO internal friction) • Is incompressible (meaning its Density is constant) • Its motion is steady and NON – TURB ...
Fluid Dynamics - cloudfront.net
... Up till now, we have pretty much focused on fluids at rest. Now let's look at fluids in motion It is important that you understand that an IDEAL FLUID: ...
... Up till now, we have pretty much focused on fluids at rest. Now let's look at fluids in motion It is important that you understand that an IDEAL FLUID: ...
Fluids - Dynamics - Physics of Papaleo
... is non-viscous No internal friction is incompressible Density R.T.S. is when its motion is steady A fluid's motion can be said to be STREAMLINE, or LAMINAR. The path itself is called the streamline. By Laminar, we mean that every particle moves exactly along the smooth path as every partic ...
... is non-viscous No internal friction is incompressible Density R.T.S. is when its motion is steady A fluid's motion can be said to be STREAMLINE, or LAMINAR. The path itself is called the streamline. By Laminar, we mean that every particle moves exactly along the smooth path as every partic ...
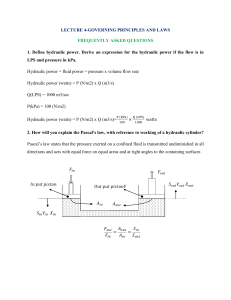
LECTURE 4-GOVERNING PRINCIPLES AND LAWS FREQUENTLY
... 4. What is continuity equation and what are its implications relative to fluid power Continuity equation states that the weight flow rate is same for all cross sections of pipe. Larger pipe gives smaller velocity and smaller pipes give larger velocity. 5. What is the significance of each term in the ...
... 4. What is continuity equation and what are its implications relative to fluid power Continuity equation states that the weight flow rate is same for all cross sections of pipe. Larger pipe gives smaller velocity and smaller pipes give larger velocity. 5. What is the significance of each term in the ...
Rotational Motion
... The kinetic energy in a fluid is the same as for any other mass: K = ½ mv2. The change in potential energy is: U = mgh. The work done on a fluid is due to pressure. • Pressure acting on a volume: W = PAx = PV. ...
... The kinetic energy in a fluid is the same as for any other mass: K = ½ mv2. The change in potential energy is: U = mgh. The work done on a fluid is due to pressure. • Pressure acting on a volume: W = PAx = PV. ...
Blade element momentum theory

Blade element momentum theory is a theory that combines both blade element theory and momentum theory. It is used to calculate the local forces on a propeller or wind-turbine blade. Blade element theory is combined with momentum theory to alleviate some of the difficulties in calculating the induced velocities at the rotor.This article emphasizes application of BEM to ground-based wind turbines, but the principles apply as well to propellers. Whereas the streamtube area is reduced by a propeller, it is expanded by a wind turbine. For either application, a highly simplified but useful approximation is the Rankine-Froude ""momentum"" or ""actuator disk"" model (1865,1889). Herein, we study the ""Betz Limit"" on the efficiency of a ground-based wind turbine.A development came in the form of Froude's Blade Element Momentum theory (1878), later refined by Glauert (1926). Betz (1921) provided an approximate correction to momentum ""Rankine-Froude Actuator-Disk"" theory to account for the sudden rotation imparted to the flow by the actuator disk (NACA TN 83, ""The Theory of the Screw Propeller"" and NACA TM 491, ""Propeller Problems""). In Blade Element Momentum theory, angular momentum is included in the model, meaning that the wake (the air after interaction with the rotor) has angular momentum. That is, the air begins to rotate about the z-axis immediately upon interaction with the rotor (see diagram below). Angular momentum must be taken into account since the rotor, which is the device that extracts the energy from the wind, is rotating as a result of the interaction with the wind.The following provides a background section on the Rankine-Froude model, followed by the Blade Element Momentum theory.