Algebra II - Net Start Class
... (10.) The perimeter of a rectangle is 108 cm. The width is one-half of the length. Find the dimensions of the rectangle. Equation 1 __________________________ Equation 2 __________________________ Solution in a complete sentence: (11.) Brad is a farmer. He feeds his hogs 12 pounds of feed per day an ...
... (10.) The perimeter of a rectangle is 108 cm. The width is one-half of the length. Find the dimensions of the rectangle. Equation 1 __________________________ Equation 2 __________________________ Solution in a complete sentence: (11.) Brad is a farmer. He feeds his hogs 12 pounds of feed per day an ...
pre-calculus - Chagrin Falls Schools
... Exponents – laws of exponents, negative exponents, fractional exponents Inverse of Functions – limit range of inverse (to make it one-to-one) Equations of Lines – point-slope form, parallel or perpendicular lines Laws of Sines and Cosines – for acute and obtuse triangles Area of a Triangle ...
... Exponents – laws of exponents, negative exponents, fractional exponents Inverse of Functions – limit range of inverse (to make it one-to-one) Equations of Lines – point-slope form, parallel or perpendicular lines Laws of Sines and Cosines – for acute and obtuse triangles Area of a Triangle ...
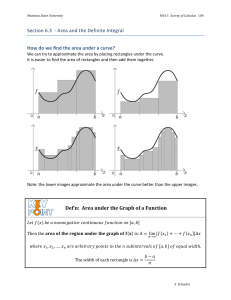
Section 6.3 -‐ Area and the Definite Integral How do we find the a
... We can try to approximate the area by placing rectangles under the curve. It is easier to find the area of rectangles and then add them together. ...
... We can try to approximate the area by placing rectangles under the curve. It is easier to find the area of rectangles and then add them together. ...
The Calculus of Variations: An Introduction
... “Calculus of variations seeks to find the path, curve, surface, etc., for which a given function has a stationary value (which, in physical problems, is usually a minimum or maximum).” (MathWorld Website) Variational calculus had its beginnings in ...
... “Calculus of variations seeks to find the path, curve, surface, etc., for which a given function has a stationary value (which, in physical problems, is usually a minimum or maximum).” (MathWorld Website) Variational calculus had its beginnings in ...
Chapter 9 Geometric Applications of Definite Integrals
... EXAMPLE 2 Find the surface area of a torus which is generated by revolving a circle of radius a about a line in its plane at a distance b from its centre, where b > a. EXAMPLE 3 The area bounded by the y-axis and the curves whose equations are x2 = 4y and x 2y + 4 = 0 is revolved about the y-axis. ...
... EXAMPLE 2 Find the surface area of a torus which is generated by revolving a circle of radius a about a line in its plane at a distance b from its centre, where b > a. EXAMPLE 3 The area bounded by the y-axis and the curves whose equations are x2 = 4y and x 2y + 4 = 0 is revolved about the y-axis. ...
Section 1 (Answers may vary) 1. In no more than 50 words, how
... (2 points) A weightlifter hoists a barbell above his head. The total length of the bar is 2 meters. Eighty kg of weight are added to each side, with the center of the weights lying .23 m from the outside tip of the bar on both sides. If the barbell was hoisted from the very center of the bar, what w ...
... (2 points) A weightlifter hoists a barbell above his head. The total length of the bar is 2 meters. Eighty kg of weight are added to each side, with the center of the weights lying .23 m from the outside tip of the bar on both sides. If the barbell was hoisted from the very center of the bar, what w ...
Form Properties24
... 1) The curve is symmetric about the y-axis when f (-x) = f (x) for all x in D. This function f is called even function. Examples: y = x2, y = x4, y = | x |, and y = cos x. 2) The curve is symmetric about the origin when f (-x) = -f (x) for all x in D. This function f is called odd function. Examples ...
... 1) The curve is symmetric about the y-axis when f (-x) = f (x) for all x in D. This function f is called even function. Examples: y = x2, y = x4, y = | x |, and y = cos x. 2) The curve is symmetric about the origin when f (-x) = -f (x) for all x in D. This function f is called odd function. Examples ...
1.2 Using Segments and Congruence
... For example, if you align S with 2, T appears to align with 5.4. ...
... For example, if you align S with 2, T appears to align with 5.4. ...
10.6 Translating Conic Sections
... Write an equation of a hyperbola with vertices (–1, 2) and (3, 2), and foci (–3, 2) and (5, 2). Draw a sketch. The center is the midpoint of the line joining the vertices. Its coordinates are (1, 2). The distance between the vertices is 2a, and the distance between the foci is 2c. 2a = 4, so a = 2; ...
... Write an equation of a hyperbola with vertices (–1, 2) and (3, 2), and foci (–3, 2) and (5, 2). Draw a sketch. The center is the midpoint of the line joining the vertices. Its coordinates are (1, 2). The distance between the vertices is 2a, and the distance between the foci is 2c. 2a = 4, so a = 2; ...
Sections 6.1-6.5 Review #1
... What point on the image corresponds to this point? ________________ 3. True or False. The image is congruent to the preimage. _______________________ Consider the parabola with the equation y+ 3 = 3(x+ 4)2 4. What is its vertex? __________________ 5. What is the equation of the axis of symmetry? ...
... What point on the image corresponds to this point? ________________ 3. True or False. The image is congruent to the preimage. _______________________ Consider the parabola with the equation y+ 3 = 3(x+ 4)2 4. What is its vertex? __________________ 5. What is the equation of the axis of symmetry? ...
PreCalculus
... 1. Pre-Calculus is a pre-requisite for this course. What mathematics course and what curriculum are you using currently (please indicate if it is with TPS)? 2. How are you testing? What is the average course grade currently? 3. What is your child's general attitude toward mathematics? 4. What percen ...
... 1. Pre-Calculus is a pre-requisite for this course. What mathematics course and what curriculum are you using currently (please indicate if it is with TPS)? 2. How are you testing? What is the average course grade currently? 3. What is your child's general attitude toward mathematics? 4. What percen ...
09 Neutral Geometry I
... vary a little from Euclid’s approach, but not much. Euclid started with giving a list of definitions. In modern formalism, we realize that we can’t quite define all the things the way Euclid did, and that some things have to be left undefined. Euclid’s attempts at definitions of these terms will ind ...
... vary a little from Euclid’s approach, but not much. Euclid started with giving a list of definitions. In modern formalism, we realize that we can’t quite define all the things the way Euclid did, and that some things have to be left undefined. Euclid’s attempts at definitions of these terms will ind ...
9.3 Ellipses 1. Describe the equation for an ellipse. How does it
... xy terms is a bit more complex. We will not plot equations with xy terms, but when you encounter one you need to recognize what type of conic section it is. Example: Which conic section will the following equation be? x 2 + 4 xy + y 2 −10x − 8y + 16 = 0 ...
... xy terms is a bit more complex. We will not plot equations with xy terms, but when you encounter one you need to recognize what type of conic section it is. Example: Which conic section will the following equation be? x 2 + 4 xy + y 2 −10x − 8y + 16 = 0 ...
PARAMETERIZATIONS OF PLANE CURVES Suppose we want to
... Suppose we want to plot the path of a particle moving in a plane. This path looks like a curve, but we cannot plot it like we would plot any other type of curve in the Cartesian plane. The reason for this is the fact that we cannot express y directly in terms of x or x in terms of y. To get around t ...
... Suppose we want to plot the path of a particle moving in a plane. This path looks like a curve, but we cannot plot it like we would plot any other type of curve in the Cartesian plane. The reason for this is the fact that we cannot express y directly in terms of x or x in terms of y. To get around t ...
Internal geometry of surfaces
... Nikolai Lobachevsky in 1829 and Janos Bolyai in 1831 published accounts of acute (hyperbolic) geometry, which were later developed by Lobachevsky, Riemann and Poincare. The independence of the parallel postulate from Euclid’s other axioms was finally demonstrated by Eugenio Beltrami in 1868. ...
... Nikolai Lobachevsky in 1829 and Janos Bolyai in 1831 published accounts of acute (hyperbolic) geometry, which were later developed by Lobachevsky, Riemann and Poincare. The independence of the parallel postulate from Euclid’s other axioms was finally demonstrated by Eugenio Beltrami in 1868. ...
Geometry Choice Board
... Go to the following website and follow the activity. At the end, answer all practice problems. ...
... Go to the following website and follow the activity. At the end, answer all practice problems. ...
Mathematical Terms 1 (Geometry) Angle – angles are formed by two
... Plane - when a set of points joined together form a flat surface, the plane can extend without end in all directions. Polygon - line segments joined together to form a closed figure. Rectangles, squares, pentagons are all examples of polygons. Quadrant - one quarter (qua) of the plane on the cartesi ...
... Plane - when a set of points joined together form a flat surface, the plane can extend without end in all directions. Polygon - line segments joined together to form a closed figure. Rectangles, squares, pentagons are all examples of polygons. Quadrant - one quarter (qua) of the plane on the cartesi ...
Additional Mathematics Paper 1 2006 June (IGCSE) - Star
... The line y + 4x = 23 intersects the curve xy + x = 20 at two points, A and B. Find the equation of the perpendicular bisector of the line AB. ...
... The line y + 4x = 23 intersects the curve xy + x = 20 at two points, A and B. Find the equation of the perpendicular bisector of the line AB. ...
Chapter 2 Macromolecules
... Important Concepts: end-to-end distance, radius of gyration, Kuhn length, persistence length, scaling The simplest model of polymer conformation treats the molecule as a chain of rigid subunits, joined by perfectly flexible hinges [20]. In this freely jointed chain model the chain is made up of N li ...
... Important Concepts: end-to-end distance, radius of gyration, Kuhn length, persistence length, scaling The simplest model of polymer conformation treats the molecule as a chain of rigid subunits, joined by perfectly flexible hinges [20]. In this freely jointed chain model the chain is made up of N li ...
At x - Year11IB
... (x – 1) is not a factor Try (x + 1): Test P(-1) = (-1)3 + 4(-1)2 – 7(-1) – 10 = 0 (x + 1) is a factor Try (x – 2): Test P(2) = (2)3 + 4(2)2 – 7(2) – 10 = 0 (x - 2) is a factor If (x + 1) and (x – 2) are factors then (x + 5) must be the third factor (1 x –2 x 5 = -10) ...
... (x – 1) is not a factor Try (x + 1): Test P(-1) = (-1)3 + 4(-1)2 – 7(-1) – 10 = 0 (x + 1) is a factor Try (x – 2): Test P(2) = (2)3 + 4(2)2 – 7(2) – 10 = 0 (x - 2) is a factor If (x + 1) and (x – 2) are factors then (x + 5) must be the third factor (1 x –2 x 5 = -10) ...
Things to remember about points, lines, segments, rays and planes
... 3. The intersection of two planes is a __________. 4. Opposite rays have the same ____________________ and __________________________. __________ and __________ are opposite rays. ...
... 3. The intersection of two planes is a __________. 4. Opposite rays have the same ____________________ and __________________________. __________ and __________ are opposite rays. ...
Algebra I Review Sheet: Name 1. Translate into an equation: 5 less
... a $5 sign-up fee and the cost to download each game is $2. How many games can the child download if they have $35? ...
... a $5 sign-up fee and the cost to download each game is $2. How many games can the child download if they have $35? ...
Catenary
In physics and geometry, a catenary[p] is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends. The curve has a U-like shape, superficially similar in appearance to a parabola, but it is not a parabola: it is a (scaled, rotated) graph of the hyperbolic cosine. The curve appears in the design of certain types of arches and as a cross section of the catenoid—the shape assumed by a soap film bounded by two parallel circular rings.The catenary is also called the alysoid, chainette, or, particularly in the material sciences, funicular.Mathematically, the catenary curve is the graph of the hyperbolic cosine function. The surface of revolution of the catenary curve, the catenoid, is a minimal surface, specifically a minimal surface of revolution. The mathematical properties of the catenary curve were first studied by Robert Hooke in the 1670s, and its equation was derived by Leibniz, Huygens and Johann Bernoulli in 1691.Catenaries and related curves are used in architecture and engineering, in the design of bridges and arches, so that forces do not result in bending moments. In the offshore oil and gas industry, 'catenary' refers to a steel catenary riser, a pipeline suspended between a production platform and the seabed that adopts an approximate catenary shape.