Lesson 2.4: Angle Properties in Polygons, page 99
... S(10) = 144° 12. a) e.g., A test could be a single line drawn anywhere through the polygon. For convex polygons, it intersects two sides only. For nonconvex polygons, it can intersect in more than two sides. b) If any diagonal is exterior to the polygon, the polygon is non-convex. 13. a) Assume the ...
... S(10) = 144° 12. a) e.g., A test could be a single line drawn anywhere through the polygon. For convex polygons, it intersects two sides only. For nonconvex polygons, it can intersect in more than two sides. b) If any diagonal is exterior to the polygon, the polygon is non-convex. 13. a) Assume the ...
Symmetry and Tessellations
... rhombus. Write down all the things you observe about this new figure. (i.e. angles, lengths of sides, diagonals, symmetry etc.) 6. Use two of the triangles to form a rectangle. Record your observations. 7. Use four of the triangles to form a rhombus. Record your observations. 8. Use all four of the ...
... rhombus. Write down all the things you observe about this new figure. (i.e. angles, lengths of sides, diagonals, symmetry etc.) 6. Use two of the triangles to form a rectangle. Record your observations. 7. Use four of the triangles to form a rhombus. Record your observations. 8. Use all four of the ...
A Congruence Problem for Polyhedra
... be allowed. For example, in much of the paper, allowed measurements will include distances between pairs of vertices, angles between edges, angles between two intersecting face diagonals (possibly on different faces with a common vertex) or between a face diagonal and an edge, and dihedral angles (t ...
... be allowed. For example, in much of the paper, allowed measurements will include distances between pairs of vertices, angles between edges, angles between two intersecting face diagonals (possibly on different faces with a common vertex) or between a face diagonal and an edge, and dihedral angles (t ...
Geometry Indicators
... B. A semiregular polyhedron is a solid that has faces in the shape of more than one kind of regular polygon, each vertex is surrounded by the same kinds of polygons in the same order, and each edge is congruent. Construct a truncated cube (a cube with its corners cut off) that is semiregular from a ...
... B. A semiregular polyhedron is a solid that has faces in the shape of more than one kind of regular polygon, each vertex is surrounded by the same kinds of polygons in the same order, and each edge is congruent. Construct a truncated cube (a cube with its corners cut off) that is semiregular from a ...
Unit 13 - Connecticut Core Standards
... Parallel Lines Corresponding Angles Theorem. It is an opportunity to solidify understanding of the relationship between a conditional statement and its converse. In addition, the converse is used to justify the compass and straightedge construction of a line through a given point parallel to a given ...
... Parallel Lines Corresponding Angles Theorem. It is an opportunity to solidify understanding of the relationship between a conditional statement and its converse. In addition, the converse is used to justify the compass and straightedge construction of a line through a given point parallel to a given ...
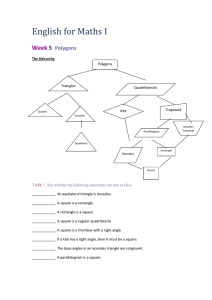
English for Maths I
... TASK 1. Say whether the following statements are true or false. ____________ An equilateral triangle is isosceles ____________ A square is a rectangle ____________ A rectangle is a square ____________ A square is a regular quadrilateral ____________ A square is a rhombus with a right angle _________ ...
... TASK 1. Say whether the following statements are true or false. ____________ An equilateral triangle is isosceles ____________ A square is a rectangle ____________ A rectangle is a square ____________ A square is a regular quadrilateral ____________ A square is a rhombus with a right angle _________ ...
shapes and angles
... Tessellations Two shapes tessellate if they fit together (like tiles) with no gap in between them. The way to check if shapes tessellate it to either draw them to scale (the hard way) or you can check if you can place the angles together and get 360o. Example You can see these shapes tessellate as ...
... Tessellations Two shapes tessellate if they fit together (like tiles) with no gap in between them. The way to check if shapes tessellate it to either draw them to scale (the hard way) or you can check if you can place the angles together and get 360o. Example You can see these shapes tessellate as ...
DOMINO TILINGS AND DETERMINANTS V. Aksenov and K. Kokhas
... Let us remind the definition of the pfaffian. For each pair of vertices of an undirected graph G we fix the order in which the vertices of this pair should be written. We may assume that the vertices of the graph are numbered and, therefore, the corresponding order is given for each pair of numbers. The ...
... Let us remind the definition of the pfaffian. For each pair of vertices of an undirected graph G we fix the order in which the vertices of this pair should be written. We may assume that the vertices of the graph are numbered and, therefore, the corresponding order is given for each pair of numbers. The ...
Ch 8 Notes
... properties of quadrilaterals, and the properties of circles. 12.0 Students find and use measures of sides and of interior and exterior angles of triangles and polygons to classify figures and solve problems. ...
... properties of quadrilaterals, and the properties of circles. 12.0 Students find and use measures of sides and of interior and exterior angles of triangles and polygons to classify figures and solve problems. ...
Answer
... The sum of the measures of five interior angles of a heptagon is 690. The measure of the 6th angle is twice the measure of the seventh. Find the measure of the 6th angle. Answer ...
... The sum of the measures of five interior angles of a heptagon is 690. The measure of the 6th angle is twice the measure of the seventh. Find the measure of the 6th angle. Answer ...
Chap 4 homework packet
... HW #23: Problems #15 - 33 Choose the best answer for each multiple choice question 15.) All of the following are ways to prove triangles congruent except? ...
... HW #23: Problems #15 - 33 Choose the best answer for each multiple choice question 15.) All of the following are ways to prove triangles congruent except? ...
similar polygons
... 7-1 Ratios in Similar Polygons A similarity ratio is the ratio of the lengths of the corresponding sides of two similar polygons. The similarity ratio of ∆ABC to ∆DEF is ...
... 7-1 Ratios in Similar Polygons A similarity ratio is the ratio of the lengths of the corresponding sides of two similar polygons. The similarity ratio of ∆ABC to ∆DEF is ...
Exterior Angles
... Angles in a triangle • Sum of angles in a triangle: Adding all the angles in a triangle gives 180°. • Remote Interior angles of a triangle: The two non adjacent angles to the exterior angle. • Exterior angle inequality: An exterior angle of a triangle is greater than either of the remote interior ...
... Angles in a triangle • Sum of angles in a triangle: Adding all the angles in a triangle gives 180°. • Remote Interior angles of a triangle: The two non adjacent angles to the exterior angle. • Exterior angle inequality: An exterior angle of a triangle is greater than either of the remote interior ...
List of regular polytopes and compounds
This page lists the regular polytopes and regular polytope compounds in Euclidean, spherical and hyperbolic spaces.The Schläfli symbol describes every regular tessellation of an n-sphere, Euclidean and hyperbolic spaces. A Schläfli symbol describing an n-polytope equivalently describes a tessellation of a (n-1)-sphere. In addition, the symmetry of a regular polytope or tessellation is expressed as a Coxeter group, which Coxeter expressed identically to the Schläfli symbol, except delimiting by square brackets, a notation that is called Coxeter notation. Another related symbol is the Coxeter-Dynkin diagram which represents a symmetry group with no rings, and the represents regular polytope or tessellation with a ring on the first node. For example the cube has Schläfli symbol {4,3}, and with its octahedral symmetry, [4,3] or File:CDel node.pngFile:CDel 4.pngFile:CDel node.pngFile:CDel 3.pngFile:CDel node.png, is represented by Coxeter diagram File:CDel node 1.pngFile:CDel 4.pngFile:CDel node.pngFile:CDel 3.pngFile:CDel node.png.The regular polytopes are grouped by dimension and subgrouped by convex, nonconvex and infinite forms. Nonconvex forms use the same vertices as the convex forms, but have intersecting facets. Infinite forms tessellate a one-lower-dimensional Euclidean space.Infinite forms can be extended to tessellate a hyperbolic space. Hyperbolic space is like normal space at a small scale, but parallel lines diverge at a distance. This allows vertex figures to have negative angle defects, like making a vertex with seven equilateral triangles and allowing it to lie flat. It cannot be done in a regular plane, but can be at the right scale of a hyperbolic plane.A more general definition of regular polytopes which do not have simple Schläfli symbols includes regular skew polytopes and regular skew apeirotopes with nonplanar facets or vertex figures.