On Lobachevsky`s trigonometric formulae
... details, and highlighting applications of his work outside the world of pure geometry,6 with the hope of attracting the attention of his colleagues. His efforts in that direction were vain, and his work was acknowledged only ten years after his death. These memoirs that he left, despite the fact tha ...
... details, and highlighting applications of his work outside the world of pure geometry,6 with the hope of attracting the attention of his colleagues. His efforts in that direction were vain, and his work was acknowledged only ten years after his death. These memoirs that he left, despite the fact tha ...
Slide 1
... goes through the midpoint and is perpendicular to the side What do you call the intersection of the perpendicular bisectors? ...
... goes through the midpoint and is perpendicular to the side What do you call the intersection of the perpendicular bisectors? ...
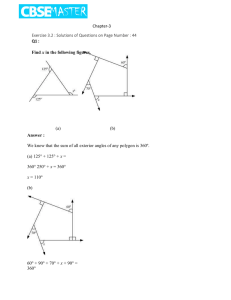
Answer - CBSEMASTER
... Here, quadrilateral ABCD (kite) has two of its interior angles, ∠ B and ∠ D, of same measures. However, still the quadrilateral ABCD is not a parallelogram as the measures of the remaining pair of opposite angles, ∠ A and ∠ C, are not equal. ...
... Here, quadrilateral ABCD (kite) has two of its interior angles, ∠ B and ∠ D, of same measures. However, still the quadrilateral ABCD is not a parallelogram as the measures of the remaining pair of opposite angles, ∠ A and ∠ C, are not equal. ...
Construct a regular hexagon in as few steps as possible. Construction
... radii congruent to line segment AB. Therefore, line segments AB, BC, CD, EF, FA, AO, BO, CO, DO, EO, and FO are all congruent to one another because they are radii of congruent circles. Therefore, triangles AOB, BOC, COD, EOF, and FOA are all congruent to one another by I.8 (SSS), and they are also ...
... radii congruent to line segment AB. Therefore, line segments AB, BC, CD, EF, FA, AO, BO, CO, DO, EO, and FO are all congruent to one another because they are radii of congruent circles. Therefore, triangles AOB, BOC, COD, EOF, and FOA are all congruent to one another by I.8 (SSS), and they are also ...
Non-Euclidean Geometry Unit
... plane geometry, the basic concepts are points and lines. In spherical geometry, points are defined in the usual way, but lines are defined such that the shortest distance between two points lies along them. Therefore, lines in spherical geometry are Great Circles. A Great Circle is the largest circl ...
... plane geometry, the basic concepts are points and lines. In spherical geometry, points are defined in the usual way, but lines are defined such that the shortest distance between two points lies along them. Therefore, lines in spherical geometry are Great Circles. A Great Circle is the largest circl ...
All the corresponding sides are congruent. All the corresponding
... What makes two figures congruent? All the corresponding sides are congruent. All the corresponding angles are congruent. ...
... What makes two figures congruent? All the corresponding sides are congruent. All the corresponding angles are congruent. ...
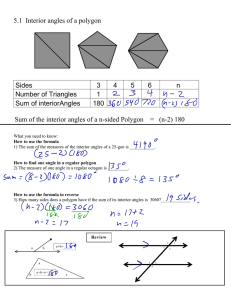
5.1 Interior angles of a polygon Sides 3 4 5 6 n Number of Triangles
... 1. If the sum of the measures of two angles is 90°, then the angles are __________________. 2. In an isosceles triangle, the base angles are _________________. 3. The sum of the measures of the angles of an octagon is _____________________. 4. Each angle of a regular hexagon measures _______________ ...
... 1. If the sum of the measures of two angles is 90°, then the angles are __________________. 2. In an isosceles triangle, the base angles are _________________. 3. The sum of the measures of the angles of an octagon is _____________________. 4. Each angle of a regular hexagon measures _______________ ...
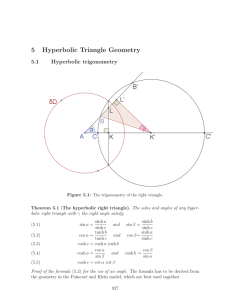
Triangles in Hyperbolic Geometry
... two points. Definition 2.2 (Postulate 2). A straight line segment can be extended indefinitely in a straight line. Definition 2.3 (Postulate 3). Given a straight line segment, a circle can be drawn using the segment as radius and one endpoint as center. Definition 2.4 (Postulate 4). All right angles ...
... two points. Definition 2.2 (Postulate 2). A straight line segment can be extended indefinitely in a straight line. Definition 2.3 (Postulate 3). Given a straight line segment, a circle can be drawn using the segment as radius and one endpoint as center. Definition 2.4 (Postulate 4). All right angles ...
List of regular polytopes and compounds
This page lists the regular polytopes and regular polytope compounds in Euclidean, spherical and hyperbolic spaces.The Schläfli symbol describes every regular tessellation of an n-sphere, Euclidean and hyperbolic spaces. A Schläfli symbol describing an n-polytope equivalently describes a tessellation of a (n-1)-sphere. In addition, the symmetry of a regular polytope or tessellation is expressed as a Coxeter group, which Coxeter expressed identically to the Schläfli symbol, except delimiting by square brackets, a notation that is called Coxeter notation. Another related symbol is the Coxeter-Dynkin diagram which represents a symmetry group with no rings, and the represents regular polytope or tessellation with a ring on the first node. For example the cube has Schläfli symbol {4,3}, and with its octahedral symmetry, [4,3] or File:CDel node.pngFile:CDel 4.pngFile:CDel node.pngFile:CDel 3.pngFile:CDel node.png, is represented by Coxeter diagram File:CDel node 1.pngFile:CDel 4.pngFile:CDel node.pngFile:CDel 3.pngFile:CDel node.png.The regular polytopes are grouped by dimension and subgrouped by convex, nonconvex and infinite forms. Nonconvex forms use the same vertices as the convex forms, but have intersecting facets. Infinite forms tessellate a one-lower-dimensional Euclidean space.Infinite forms can be extended to tessellate a hyperbolic space. Hyperbolic space is like normal space at a small scale, but parallel lines diverge at a distance. This allows vertex figures to have negative angle defects, like making a vertex with seven equilateral triangles and allowing it to lie flat. It cannot be done in a regular plane, but can be at the right scale of a hyperbolic plane.A more general definition of regular polytopes which do not have simple Schläfli symbols includes regular skew polytopes and regular skew apeirotopes with nonplanar facets or vertex figures.