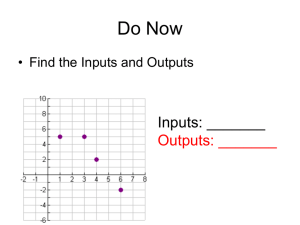
basic counting
... c (for continuum). We know that c is greater than א0, but it is unknown whether c=א1. This proposition (that c=א1) is called the continuum hypothesis. It was shown in the 20th century to be independent of the axioms of set theory. That means that it does not contradict them nor can it be prov ...
... c (for continuum). We know that c is greater than א0, but it is unknown whether c=א1. This proposition (that c=א1) is called the continuum hypothesis. It was shown in the 20th century to be independent of the axioms of set theory. That means that it does not contradict them nor can it be prov ...
PowerPoint
... Law of large numbers (this is true!) If an event is repeated many times independently with the same probability of success each time, the long-run success proportion will approach that probability. • With independent events, knowing what has happened tells you nothing about what will happen. Misund ...
... Law of large numbers (this is true!) If an event is repeated many times independently with the same probability of success each time, the long-run success proportion will approach that probability. • With independent events, knowing what has happened tells you nothing about what will happen. Misund ...
Discrete Event Simulation
... the essential characteristics of a real system. Simulations may be deterministic or stochastic, static or dynamic, continuous or discrete. Discrete event simulation (DEVS) is stochastic, dynamic, and discrete. DEVS is not necessarily spatial – it usually isn’t, but the ideas are applicable to ...
... the essential characteristics of a real system. Simulations may be deterministic or stochastic, static or dynamic, continuous or discrete. Discrete event simulation (DEVS) is stochastic, dynamic, and discrete. DEVS is not necessarily spatial – it usually isn’t, but the ideas are applicable to ...
simulation
... the essential characteristics of a real system. Simulations may be deterministic or stochastic, static or dynamic, continuous or discrete. Discrete event simulation (DEVS) is stochastic, dynamic, and discrete. DEVS is not necessarily spatial – it usually isn’t, but the ideas are applicable to ...
... the essential characteristics of a real system. Simulations may be deterministic or stochastic, static or dynamic, continuous or discrete. Discrete event simulation (DEVS) is stochastic, dynamic, and discrete. DEVS is not necessarily spatial – it usually isn’t, but the ideas are applicable to ...
CLEP® College Mathematics: At a Glance
... the topics in the outline above, but the approaches to certain topics and the emphases given to them may differ. To prepare for the College Mathematics exam, it is advisable to study one or more introductory college-level mathematics textbooks, ...
... the topics in the outline above, but the approaches to certain topics and the emphases given to them may differ. To prepare for the College Mathematics exam, it is advisable to study one or more introductory college-level mathematics textbooks, ...
Teaching Graph Theory and its Applications: An Approach for the
... All students will develop an understanding of the concepts and techniques of analysis, probability, and discrete mathematics, and will use them to model situations, solve problems, and analyze and draw appropriate inferences from data. ...
... All students will develop an understanding of the concepts and techniques of analysis, probability, and discrete mathematics, and will use them to model situations, solve problems, and analyze and draw appropriate inferences from data. ...
Syllabus - Gurukula Kangri Vishwavidyalaya, Haridwar
... Finite Element Analysis, Integral formulations and variational methods, Finite element discretization of continuum, Shape functions, Element matrices, Finite element methods for boundary value problems of ordinary and partial differential equations. Practical: Practical on numerical computation of t ...
... Finite Element Analysis, Integral formulations and variational methods, Finite element discretization of continuum, Shape functions, Element matrices, Finite element methods for boundary value problems of ordinary and partial differential equations. Practical: Practical on numerical computation of t ...
Problems set
... D.8.3 Determine whether two propositions are logically equivalent. D.8.4 Identify and give examples of undefined terms, definitions, axioms, and theorems. D.8.5 Construct logical arguments using laws of detachment, syllogism, tautology, and contradiction; judge the validity of arguments, and give c ...
... D.8.3 Determine whether two propositions are logically equivalent. D.8.4 Identify and give examples of undefined terms, definitions, axioms, and theorems. D.8.5 Construct logical arguments using laws of detachment, syllogism, tautology, and contradiction; judge the validity of arguments, and give c ...
HOSTOS COMMUNITY COLLEGE DEPARTMENT OF MATHEMATICS MAT 100
... 5. Evaluate solutions to problems for reasonableness. Recognize patterns and use these patterns for predicting the general term in a sequence. ...
... 5. Evaluate solutions to problems for reasonableness. Recognize patterns and use these patterns for predicting the general term in a sequence. ...
Non-standard Simplex Problems
... Steps 1: Simplex Method for Non-Standard Problems 1. If neccessary, rewrite the problem as a max. Minimizing C is equivalent as maximizing −C 2. If necessary, rewrite all constraints using ≤ signs 3. Introduce slack variables and set up initial simplex table 4. Scan the column of constants for negat ...
... Steps 1: Simplex Method for Non-Standard Problems 1. If neccessary, rewrite the problem as a max. Minimizing C is equivalent as maximizing −C 2. If necessary, rewrite all constraints using ≤ signs 3. Introduce slack variables and set up initial simplex table 4. Scan the column of constants for negat ...
http://cc.ee.ntu.edu.tw/~farn/courses/DM/slide/Module-4-countability-gra...
... . Now, consider a real number generated by taking . all digits di,i that lie along the diagonal in this figure . and replacing them with different digits. ...
... . Now, consider a real number generated by taking . all digits di,i that lie along the diagonal in this figure . and replacing them with different digits. ...
Integers and division
... Hash function An example of a hash function that maps integers (including very large ones) to a subset of integers 0, 1, .. m-1 is: h(k) = k mod m Example: Assume we have a database of employes, each with a unique ID – a social security number that consists of 8 digits. We want to store the records ...
... Hash function An example of a hash function that maps integers (including very large ones) to a subset of integers 0, 1, .. m-1 is: h(k) = k mod m Example: Assume we have a database of employes, each with a unique ID – a social security number that consists of 8 digits. We want to store the records ...
basic counting
... setting: Recall that a permutation is a bijection f:[n]→[n], where n is a nonnegative integer. If f is a permutation and f(i)=i, then i is a fixed point of the permutation and we say that f fixes i.. For instance if n=6, the permutation 526413 has fixed points 2 and 4. A permutation without fixed po ...
... setting: Recall that a permutation is a bijection f:[n]→[n], where n is a nonnegative integer. If f is a permutation and f(i)=i, then i is a fixed point of the permutation and we say that f fixes i.. For instance if n=6, the permutation 526413 has fixed points 2 and 4. A permutation without fixed po ...
WUCT121: Discrete Mathematics Wollongong College Australia
... Number of vertices: both 5; Number of edges: both 5; Degrees of corresponding vertices: all degree 2; Connectedness: Each is fully connected; Number of connected components: Both 1; Pairs of connected vertices: All correspond; Number of loops: 0; Number of parallel edges: 0; Everything is equal and ...
... Number of vertices: both 5; Number of edges: both 5; Degrees of corresponding vertices: all degree 2; Connectedness: Each is fully connected; Number of connected components: Both 1; Pairs of connected vertices: All correspond; Number of loops: 0; Number of parallel edges: 0; Everything is equal and ...
Chapter 3. Introductory Combinatorics
... paradox 1899,Cantor's paradox, sometimes called the paradox of the greatest cardinal, expresses what its second name would imply--that there is no cardinal larger than every other cardinal. Let S be the set of all sets. |S|?|P (S)| or |P (S)|?|(S)| The Third Crisis in Mathematics ...
... paradox 1899,Cantor's paradox, sometimes called the paradox of the greatest cardinal, expresses what its second name would imply--that there is no cardinal larger than every other cardinal. Let S be the set of all sets. |S|?|P (S)| or |P (S)|?|(S)| The Third Crisis in Mathematics ...
21-127Placement - Carnegie Mellon School of Computer Science
... This exam will help us to evaluate your knowledge of basic discrete mathematics, which at CMU is taught in course 21-127 (the prefix 21 specifies the Mathematics department; the prefix 15 specifies the Computer Science department). This course is a prerequisite for 15-211, although students who scor ...
... This exam will help us to evaluate your knowledge of basic discrete mathematics, which at CMU is taught in course 21-127 (the prefix 21 specifies the Mathematics department; the prefix 15 specifies the Computer Science department). This course is a prerequisite for 15-211, although students who scor ...
Discrete Mathematics Exam - Carnegie Mellon School of Computer
... This exam will help us to evaluate your knowledge of basic discrete mathematics, which at CMU is taught in course 21-127 (the prefix 21 specifies the Mathematics department; the prefix 15 specifies the Computer Science department). This course is a prerequisite for 15-211, although students who scor ...
... This exam will help us to evaluate your knowledge of basic discrete mathematics, which at CMU is taught in course 21-127 (the prefix 21 specifies the Mathematics department; the prefix 15 specifies the Computer Science department). This course is a prerequisite for 15-211, although students who scor ...
Introduction to Discrete Structures Instructional Material
... Get 7 individuals to form the party. There are 3 girls and 4 boys in the group. One of the girls will be the birthday celebrant. The rest are visitors. It is a European party and it is customary to shake the hands of the house owner before entering their premises. Let the class observe how many hand ...
... Get 7 individuals to form the party. There are 3 girls and 4 boys in the group. One of the girls will be the birthday celebrant. The rest are visitors. It is a European party and it is customary to shake the hands of the house owner before entering their premises. Let the class observe how many hand ...
Integers and division
... • Multiplying both sides by c gives us bc = auc, so by definition, a | bc. • Thus a divides bc. ...
... • Multiplying both sides by c gives us bc = auc, so by definition, a | bc. • Thus a divides bc. ...
248.57 KB - KFUPM Resources v3
... 10. If x and y are integers and both xy and x + y are even, then both x and y are odd. 11. The set of all positive integers less than 100 can be denoted by {1, 4, 5, . . . , 99}. 12. If A = {1, 2}, then A2 = {(1, 1), (1, 2), (2, 1), (2, 2)}. 13. If A1 = {0, 2, 4, 6, 8}, A2 = {0, 1, 2, 3, 4}, and A3 ...
... 10. If x and y are integers and both xy and x + y are even, then both x and y are odd. 11. The set of all positive integers less than 100 can be denoted by {1, 4, 5, . . . , 99}. 12. If A = {1, 2}, then A2 = {(1, 1), (1, 2), (2, 1), (2, 2)}. 13. If A1 = {0, 2, 4, 6, 8}, A2 = {0, 1, 2, 3, 4}, and A3 ...
Introduction to Discrete Mathematics
... • Graphs, Relations • Degree sequence, Eulerian graphs, isomorphism • Trees • Matching • Coloring ...
... • Graphs, Relations • Degree sequence, Eulerian graphs, isomorphism • Trees • Matching • Coloring ...
Questions#2
... a) If x is a positive real number, then x 2 is a positive real number. Therefore, if a 2 is positive, where a is a real number, then a is a positive real number. b) If x 2 0 , where x is a real number, then x≠0. Let a be a real number with a 2 ≠ 0; then a ≠ 0. 2) Resolution: Computer programs have ...
... a) If x is a positive real number, then x 2 is a positive real number. Therefore, if a 2 is positive, where a is a real number, then a is a positive real number. b) If x 2 0 , where x is a real number, then x≠0. Let a be a real number with a 2 ≠ 0; then a ≠ 0. 2) Resolution: Computer programs have ...
CS311H: Discrete Mathematics Cardinality of Infinite Sets and
... Clearly, this new number R differs from each number Ri in the table in at least one digit (its i ’th digit) ...
... Clearly, this new number R differs from each number Ri in the table in at least one digit (its i ’th digit) ...
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying ""smoothly"", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not vary smoothly in this way, but have distinct, separated values. Discrete mathematics therefore excludes topics in ""continuous mathematics"" such as calculus and analysis. Discrete objects can often be enumerated by integers. More formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets (sets that have the same cardinality as subsets of the natural numbers, including rational numbers but not real numbers). However, there is no exact definition of the term ""discrete mathematics."" Indeed, discrete mathematics is described less by what is included than by what is excluded: continuously varying quantities and related notions.The set of objects studied in discrete mathematics can be finite or infinite. The term finite mathematics is sometimes applied to parts of the field of discrete mathematics that deals with finite sets, particularly those areas relevant to business.Research in discrete mathematics increased in the latter half of the twentieth century partly due to the development of digital computers which operate in discrete steps and store data in discrete bits. Concepts and notations from discrete mathematics are useful in studying and describing objects and problems in branches of computer science, such as computer algorithms, programming languages, cryptography, automated theorem proving, and software development. Conversely, computer implementations are significant in applying ideas from discrete mathematics to real-world problems, such as in operations research.Although the main objects of study in discrete mathematics are discrete objects, analytic methods from continuous mathematics are often employed as well.In the university curricula, ""Discrete Mathematics"" appeared in the 1980s, initially as a computer science support course; its contents were somewhat haphazard at the time. The curriculum has thereafter developed in conjunction to efforts by ACM and MAA into a course that is basically intended to develop mathematical maturity in freshmen; as such it is nowadays a prerequisite for mathematics majors in some universities as well. Some high-school-level discrete mathematics textbooks have appeared as well. At this level, discrete mathematics it is sometimes seen a preparatory course, not unlike precalculus in this respect.The Fulkerson Prize is awarded for outstanding papers in discrete mathematics.