Groupoids and Smarandache Groupoids
... groupoids exhibits simultaneously the properties of a semigroup and a groupoid. Such a combined study of an associative and a non associative structure has not been so far carried out. Except for the introduction of smarandacheian notions by Prof. Florentin Smarandache such types of studies would ha ...
... groupoids exhibits simultaneously the properties of a semigroup and a groupoid. Such a combined study of an associative and a non associative structure has not been so far carried out. Except for the introduction of smarandacheian notions by Prof. Florentin Smarandache such types of studies would ha ...
On linearly ordered H-closed topological semilattices
... VI.1.14 of [6] imply that ↑e and ↓e are closed subsets in S for any e ∈ S. Let E be a linearly ordered topological semilattice. Since ↓e and ↑e are closed for each e ∈ E, it follows that the topology of E refines the order topology. Thus the principal objects whick we shall consider can be alternati ...
... VI.1.14 of [6] imply that ↑e and ↓e are closed subsets in S for any e ∈ S. Let E be a linearly ordered topological semilattice. Since ↓e and ↑e are closed for each e ∈ E, it follows that the topology of E refines the order topology. Thus the principal objects whick we shall consider can be alternati ...
Representations of dynamical systems on Banach spaces
... systems and Banach spaces. A further indication for the success of this theory is the fact that it provides also a natural environment for the study of representations of topological groups and compact right topological semigroups on Banach spaces. Throughout our review there are some new results w ...
... systems and Banach spaces. A further indication for the success of this theory is the fact that it provides also a natural environment for the study of representations of topological groups and compact right topological semigroups on Banach spaces. Throughout our review there are some new results w ...
Boyarchenko on associativity.pdf
... toy model for this proof is presented in §4, which also contains some elementary preliminary remarks about a process in algebra known as “categorification”. 1.6. Finally, in §6, I will explain one reason why sometimes thinking about associativity constraints is important, from my personal (hence bia ...
... toy model for this proof is presented in §4, which also contains some elementary preliminary remarks about a process in algebra known as “categorification”. 1.6. Finally, in §6, I will explain one reason why sometimes thinking about associativity constraints is important, from my personal (hence bia ...
Semigroups and automata on infinite words
... nection between deterministic and non deterministic Büchi automata was enlightened by a deep theorem of McNaughton: a set of infinite words is recognized by a non deterministic Büchi automaton if and only if it is a finite boolean combination of sets recognized by deterministic Büchi automata. T ...
... nection between deterministic and non deterministic Büchi automata was enlightened by a deep theorem of McNaughton: a set of infinite words is recognized by a non deterministic Büchi automaton if and only if it is a finite boolean combination of sets recognized by deterministic Büchi automata. T ...
MATHEMATICS MAGAZINE
... In the parlance of recreational mathematics, Jessica sometimes wishes she were a Mad Veterinarian. Mad Vet scenarios were originally presented by Harris [7], who posed questions as to which collections of animals can be transformed by Mad Vet machines into other collections. Recently, such scenarios ...
... In the parlance of recreational mathematics, Jessica sometimes wishes she were a Mad Veterinarian. Mad Vet scenarios were originally presented by Harris [7], who posed questions as to which collections of animals can be transformed by Mad Vet machines into other collections. Recently, such scenarios ...
Invariant means on topological semigroups
... proof of this fact by modifying the proof of 2.2 in an obvious way. We note that if S and M are as in 2.5, then υS can be realized as the space of all ordinals less than or equal to Ω (with the order topology) and we have M(f) - fv(Ω) for all fe C(S). Finally, we use 2.2 to derive the following theo ...
... proof of this fact by modifying the proof of 2.2 in an obvious way. We note that if S and M are as in 2.5, then υS can be realized as the space of all ordinals less than or equal to Ω (with the order topology) and we have M(f) - fv(Ω) for all fe C(S). Finally, we use 2.2 to derive the following theo ...
Invariant means on topological semigroups
... with a Hausdorff topology for which the mapping (x, y)—>xy of S x S into S is continuous. We denote by C(S) the space of all continuous real-valued functions on S (not necessarily bounded). If a e S and fe C(S), then af and fa will denote those functions on S whose values at x e S are f(ax) and f(xa ...
... with a Hausdorff topology for which the mapping (x, y)—>xy of S x S into S is continuous. We denote by C(S) the space of all continuous real-valued functions on S (not necessarily bounded). If a e S and fe C(S), then af and fa will denote those functions on S whose values at x e S are f(ax) and f(xa ...
FROM COMMUTATIVE TO NONCOMMUTATIVE SETTINGS 1
... classes of rings, but, as is done in the commutative case, we develop everything in the setting of cancellative semigroups (and often more generally in the setting of cancellative small categories), for essentially three reasons: First, we wish to emphasize that the theory of factorizations is a pur ...
... classes of rings, but, as is done in the commutative case, we develop everything in the setting of cancellative semigroups (and often more generally in the setting of cancellative small categories), for essentially three reasons: First, we wish to emphasize that the theory of factorizations is a pur ...
Shuffle on positive varieties of languages.
... A congruence on a semigroup is a stable equivalence relation. If ∼ is a congruence on S, there is a well-defined multiplication on the quotient set S/∼ given by [s][t] = [st] where [s] denotes the ∼-class of s ∈ S. An ideal of a semigroup S is a subset I ⊆ S such that S 1 IS 1 ⊆ I. A nonempty ideal ...
... A congruence on a semigroup is a stable equivalence relation. If ∼ is a congruence on S, there is a well-defined multiplication on the quotient set S/∼ given by [s][t] = [st] where [s] denotes the ∼-class of s ∈ S. An ideal of a semigroup S is a subset I ⊆ S such that S 1 IS 1 ⊆ I. A nonempty ideal ...
On finite congruence
... Theorem 3.1. Let I = {1, 2, . . . , m}, Λ = {1, 2, . . . , n}, and P = (pij ) be an n × m matrix of 1’s and 0’s such that no row or column is identically zero, no two rows are identical, and no two columns are identical. Let S = (I × Λ) ∪ {∞} and define a binary relation on S by ...
... Theorem 3.1. Let I = {1, 2, . . . , m}, Λ = {1, 2, . . . , n}, and P = (pij ) be an n × m matrix of 1’s and 0’s such that no row or column is identically zero, no two rows are identical, and no two columns are identical. Let S = (I × Λ) ∪ {∞} and define a binary relation on S by ...
PARTIALIZATION OF CATEGORIES AND INVERSE BRAID
... The study of inverse semigroups forms a classical part of the theory of semigroups. Several approaches to construction of inverse semigroups are known. The most abstract one seems to be the categorical approach, which was worked out in various variations in [Ho, Le, La]. In Section 2 we give a short ...
... The study of inverse semigroups forms a classical part of the theory of semigroups. Several approaches to construction of inverse semigroups are known. The most abstract one seems to be the categorical approach, which was worked out in various variations in [Ho, Le, La]. In Section 2 we give a short ...
Groups CDM Klaus Sutner Carnegie Mellon University
... The first part follows easily from the definition. For the second part note that B must contain 1: as a finite semigroup B must contain an idempotent, which must be the identity in A. The map B → B, x 7→ b · x is a permutation of B for each b ∈ B (injective implies surjective in the finite case). Bu ...
... The first part follows easily from the definition. For the second part note that B must contain 1: as a finite semigroup B must contain an idempotent, which must be the identity in A. The map B → B, x 7→ b · x is a permutation of B for each b ∈ B (injective implies surjective in the finite case). Bu ...
Physics
... This step is entirely in the spirit of [Alb 1] where semigroups on Mn are related to diffusions on Aut(MJ. These authors, however, restrict to the case of "symmetric semigroups", i.e., semigroups satisfying the detailed balance condition. While on commutative W*-algebras a minimal Markov process is ...
... This step is entirely in the spirit of [Alb 1] where semigroups on Mn are related to diffusions on Aut(MJ. These authors, however, restrict to the case of "symmetric semigroups", i.e., semigroups satisfying the detailed balance condition. While on commutative W*-algebras a minimal Markov process is ...
Topological dynamics: basic notions and examples
... We introduce the notion of a dynamical system, over a given semigroup S. This is a (compact Hausdorff) topological space on which the semigroup S operates in the sense defined in 9.3. Dynamical systems over S are closely connected to the compact right topological semigroup βS for several reasons. Fi ...
... We introduce the notion of a dynamical system, over a given semigroup S. This is a (compact Hausdorff) topological space on which the semigroup S operates in the sense defined in 9.3. Dynamical systems over S are closely connected to the compact right topological semigroup βS for several reasons. Fi ...
A NOTE ON COMPACT SEMIRINGS
... the equivalence relation a on A XB by: (a, j)a(a', f) if (1) a = a' and j=f or (2) j=f = 0. Clearly a is a closed congruence. Thus (A XB)/a is a compact connected semiring with multiplicative identity. The maximal additive subgroups of (A XB)/a are of the form (A X {b} )/a and of course totally disc ...
... the equivalence relation a on A XB by: (a, j)a(a', f) if (1) a = a' and j=f or (2) j=f = 0. Clearly a is a closed congruence. Thus (A XB)/a is a compact connected semiring with multiplicative identity. The maximal additive subgroups of (A XB)/a are of the form (A X {b} )/a and of course totally disc ...
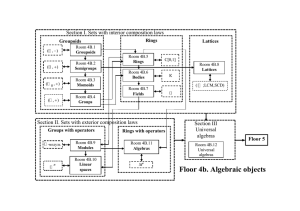
Section I. SETS WITH INTERIOR COMPOSITION LAWS
... We shall consider sets with algebraic structures. Its general notion is composition law. This is an operator, which maps a concrete quality (operation degree) of elements of the given set to an element of this set, for example, addition of numbers, sum of sets. Composition law can be interior and ex ...
... We shall consider sets with algebraic structures. Its general notion is composition law. This is an operator, which maps a concrete quality (operation degree) of elements of the given set to an element of this set, for example, addition of numbers, sum of sets. Composition law can be interior and ex ...
Minimal ideals and minimal idempotents
... To put the theory of minimal left ideals and the two sided ideal K(S) to use, we want to make sure that K(S) is non-empty, i.e. that there is at least one minimal left ideal. We prove here that in a compact right topological semigroup, even more is true: these semigroups are what we call abundant. I ...
... To put the theory of minimal left ideals and the two sided ideal K(S) to use, we want to make sure that K(S) is non-empty, i.e. that there is at least one minimal left ideal. We prove here that in a compact right topological semigroup, even more is true: these semigroups are what we call abundant. I ...
07_chapter 2
... Definition 2.2.11: A totally ordered semiring (S, +, •, ) is said to be a positively ordered in the strict sense if both (S, +, ) and (S, •, ) are positively ordered in the strict sense. Definition 2.2.12: In a t. o. s. r. (S, +, •, ) (i) (S, +) is said to be right naturally totally ordered (r. ...
... Definition 2.2.11: A totally ordered semiring (S, +, •, ) is said to be a positively ordered in the strict sense if both (S, +, ) and (S, •, ) are positively ordered in the strict sense. Definition 2.2.12: In a t. o. s. r. (S, +, •, ) (i) (S, +) is said to be right naturally totally ordered (r. ...
Homomorphisms and Topological Semigroups.
... a byn-^n^ e byNNcxbV; that is, xyNcrHCbVib e xN] and division is continuous in S. Conditions (1) and (2) above do not imply that S is a topological group. ...
... a byn-^n^ e byNNcxbV; that is, xyNcrHCbVib e xN] and division is continuous in S. Conditions (1) and (2) above do not imply that S is a topological group. ...
Weighted semigroup measure algebra as a WAP-algebra H.R. Ebrahimi Vishki, B. Khodsiani, A. Rejali
... almost periodic elements of A∗ . It is easy to verify that, W AP (A) is a (norm) closed subspace of A∗ . It is known that the multiplication of a Banach algebra A has two natural but, in general, different extensions (called Arens products) to the second dual A∗∗ each turning A∗∗ into a Banach algebr ...
... almost periodic elements of A∗ . It is easy to verify that, W AP (A) is a (norm) closed subspace of A∗ . It is known that the multiplication of a Banach algebra A has two natural but, in general, different extensions (called Arens products) to the second dual A∗∗ each turning A∗∗ into a Banach algebr ...
Course MA2C01, Michaelmas Term 2012
... are invertible are +1 and −1. Example Let n be a natural number, and let Zn = {0, 1, . . . , n − 1}. Any integer k may be expressed uniquely in the form k = qn + r for some integers q and r with 0 ≤ r < n. (When k is positive, q and r are the quotient and remainder respectively, when k is divided by ...
... are invertible are +1 and −1. Example Let n be a natural number, and let Zn = {0, 1, . . . , n − 1}. Any integer k may be expressed uniquely in the form k = qn + r for some integers q and r with 0 ≤ r < n. (When k is positive, q and r are the quotient and remainder respectively, when k is divided by ...
Graphs to semigroups
... • Graphs are assumed to be undirected. • A graph H is called a minor of a graph G if H is isomorphic to a graph that can be obtained by edge contractions from a subgraph of G. • In other words, delete some edges (and, perhaps, isolated vertices) in G, and then ...
... • Graphs are assumed to be undirected. • A graph H is called a minor of a graph G if H is isomorphic to a graph that can be obtained by edge contractions from a subgraph of G. • In other words, delete some edges (and, perhaps, isolated vertices) in G, and then ...
Polynomial closure and unambiguous product
... and inverse morphisms between free semigroups. A positive variety of languages is a class of recognizable languages closed under finite union, finite intersection, left and right quotients and inverse morphisms between free semigroups. Eilenberg’s variety theorem can be extended to positive varieti ...
... and inverse morphisms between free semigroups. A positive variety of languages is a class of recognizable languages closed under finite union, finite intersection, left and right quotients and inverse morphisms between free semigroups. Eilenberg’s variety theorem can be extended to positive varieti ...
Generating sets of finite singular transformation semigroups
... Since α1 , . . . , αr , ζi,j ∈ Dn−1 , ker(α1 ) ⊆ ker(ζi,j ) and im(ζi,j ) ⊆ im(αr ), it follows that Ker(α1 ) = Ker(ζi,j ) = {i, j }, Def(αr ) = Def(ζi,j ) = Xn \ im(ζi,j ) = {i} and that, for each 1 ≤ k ≤ r − 1, we have αk αk+1 ∈ Dn−1 . Then, from Lemma 2, we have Def(αk ) ⊆ Ker(αk+1 ). Hence there ...
... Since α1 , . . . , αr , ζi,j ∈ Dn−1 , ker(α1 ) ⊆ ker(ζi,j ) and im(ζi,j ) ⊆ im(αr ), it follows that Ker(α1 ) = Ker(ζi,j ) = {i, j }, Def(αr ) = Def(ζi,j ) = Xn \ im(ζi,j ) = {i} and that, for each 1 ≤ k ≤ r − 1, we have αk αk+1 ∈ Dn−1 . Then, from Lemma 2, we have Def(αk ) ⊆ Ker(αk+1 ). Hence there ...