Multiple Input, Multiple Output Technology
... To provide data communications over power lines, PLC must overcome many obstacles. Power distribution cables, while efficient for electricity transport, are far from ideal for data transport because they lack balanced lines and signal protection. In addition to the wiring itself not being “data com ...
... To provide data communications over power lines, PLC must overcome many obstacles. Power distribution cables, while efficient for electricity transport, are far from ideal for data transport because they lack balanced lines and signal protection. In addition to the wiring itself not being “data com ...
NeXt generation/dynamic spectrum access/cognitive radio wireless
... the permission power of an xG user can be derived, which is used for the estimation of the channel capacity The path loss increases as the operating frequency increases. Therefore, if the transmission power of an xG user remains the same, the its transmission range decreases at higher frequencies. ...
... the permission power of an xG user can be derived, which is used for the estimation of the channel capacity The path loss increases as the operating frequency increases. Therefore, if the transmission power of an xG user remains the same, the its transmission range decreases at higher frequencies. ...
Power Control for Cognitive Radio Networks
... • the dormancy of primary users; • the relative immunity of primary users with favorable channels to weak cochannel interferers. It is challenging to devise a power-control method that allows primary users to satisfy strict QoS requirements and yet is flexible enough to accommodate secondary users’ ...
... • the dormancy of primary users; • the relative immunity of primary users with favorable channels to weak cochannel interferers. It is challenging to devise a power-control method that allows primary users to satisfy strict QoS requirements and yet is flexible enough to accommodate secondary users’ ...
WWG Draft Green Book v0.117 - ccsds cwe
... The mission of the Wireless Working Group (WWG) is to serve as a general CCSDS focus group for wireless technologies. The WWG investigates and makes recommendations pursuant to standardization of applicable wireless network protocols, ensuring the interoperability of independently developed wireless ...
... The mission of the Wireless Working Group (WWG) is to serve as a general CCSDS focus group for wireless technologies. The WWG investigates and makes recommendations pursuant to standardization of applicable wireless network protocols, ensuring the interoperability of independently developed wireless ...
ppt
... Channel spectrum divided into frequency bands Each station assigned fixed frequency band Unused transmission time in frequency bands go idle Example: 6-station LAN, 1,3,4 have pkt, frequency ...
... Channel spectrum divided into frequency bands Each station assigned fixed frequency band Unused transmission time in frequency bands go idle Example: 6-station LAN, 1,3,4 have pkt, frequency ...
FullText
... Interference management is a challenging issue in the femtocells environment, especially in the case of dense deployment. The dense deployment of low power nodes is one of the main features of 4G future networks. It is very important and efficient that the performance of these nodes does not degrade ...
... Interference management is a challenging issue in the femtocells environment, especially in the case of dense deployment. The dense deployment of low power nodes is one of the main features of 4G future networks. It is very important and efficient that the performance of these nodes does not degrade ...
Presentation Slide Deck in Powerpoint 2007 Format
... The EPC core interconnect with legacy 2G/3G PS core by S3/S4 interface. In this solution, the existing SGSN should be upgraded to become S4 SGSN and the existing GGSN should be upgraded to become SAE GW. The serving gateway becomes the common anchoring point between LTE and 2G/3G. In this case, the ...
... The EPC core interconnect with legacy 2G/3G PS core by S3/S4 interface. In this solution, the existing SGSN should be upgraded to become S4 SGSN and the existing GGSN should be upgraded to become SAE GW. The serving gateway becomes the common anchoring point between LTE and 2G/3G. In this case, the ...
LTE Radio Planning
... TTI, even if the codes are not all supported by a given end-user’s device. For instance, three users with a five-code device can be served simultaneously during the same TTI. Code multiplexing also enables combined transmissions when several users’ RBSbuffered Code multiplexing With HSDPA, data tran ...
... TTI, even if the codes are not all supported by a given end-user’s device. For instance, three users with a five-code device can be served simultaneously during the same TTI. Code multiplexing also enables combined transmissions when several users’ RBSbuffered Code multiplexing With HSDPA, data tran ...
UNIT III PART-A
... Coaxial transmission line with one source and one load Impedance bridging is unsuitable for RF connections, because it causes power to be reflected back to the source from the boundary between the high and the low impedances. The reflection creates a standing wave if there is reflection at both ends ...
... Coaxial transmission line with one source and one load Impedance bridging is unsuitable for RF connections, because it causes power to be reflected back to the source from the boundary between the high and the low impedances. The reflection creates a standing wave if there is reflection at both ends ...
Joint Wideband Spectrum Sensing in Frequency Overlapping Cognitive Radio Networks Using
... and singular value decomposition methods are used for wideband spectrum sensing purpose. These approaches provide wideband spectrum sensing in a simple individual network. To eliminate the need of high speed analog to digital converters and digital signal processors in wideband sensing, techniques s ...
... and singular value decomposition methods are used for wideband spectrum sensing purpose. These approaches provide wideband spectrum sensing in a simple individual network. To eliminate the need of high speed analog to digital converters and digital signal processors in wideband sensing, techniques s ...
Systematic Design of Space-Time Trellis Codes for Wireless
... – The D2D users occupies the vacant cellular spectrum for communication. – completely eliminates cross-layer interference is to divide the licensed spectrum into two parts (orthogonal channel assignment). – a fraction of the subchannels would be used by the cellular users while another fraction woul ...
... – The D2D users occupies the vacant cellular spectrum for communication. – completely eliminates cross-layer interference is to divide the licensed spectrum into two parts (orthogonal channel assignment). – a fraction of the subchannels would be used by the cellular users while another fraction woul ...
Evolution of Cellular Technologies
... Users worldwide are finding that having broadband access to the Internet dramatically changes how we share information, conduct business, and seek entertainment. Broadband access not only provides faster Web-surfing and quicker downloading but also enables several multimedia applications, such as real ...
... Users worldwide are finding that having broadband access to the Internet dramatically changes how we share information, conduct business, and seek entertainment. Broadband access not only provides faster Web-surfing and quicker downloading but also enables several multimedia applications, such as real ...
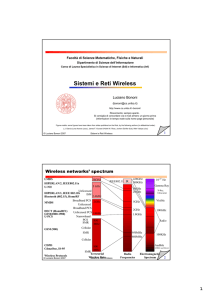
Sistemi e Reti Wireless - Dipartimento di Informatica
... • adaptive behavior of network protocols (from the wireless side) • the wired host does not know if the other host is wireless and dialogue with it in the standard wireless way (protocol transparency) • the wireless host know it is wireless and implements adaptive behavior ...
... • adaptive behavior of network protocols (from the wireless side) • the wired host does not know if the other host is wireless and dialogue with it in the standard wireless way (protocol transparency) • the wireless host know it is wireless and implements adaptive behavior ...
Coverage or Capacity—Making the Best Use of 802.11n
... for selectively tuning the performance characteristics of access points to meet different use cases and price points. These options can range from a single radio with single antenna supporting only one spatial stream, to a 4x4 MIMO configuration with four antennas and four spatial streams. For high ...
... for selectively tuning the performance characteristics of access points to meet different use cases and price points. These options can range from a single radio with single antenna supporting only one spatial stream, to a 4x4 MIMO configuration with four antennas and four spatial streams. For high ...
Signal Decoding and Receiver Evolution
... Pfennig, 1998; Ryan, 1998]. Thus it is interesting to understand how the above variables influence not only the accuracy with which the receiver can discriminate between conspecific and heterospecifics, but also how the receiver responds to conspecific signal variation. An Artificial Neural Network ...
... Pfennig, 1998; Ryan, 1998]. Thus it is interesting to understand how the above variables influence not only the accuracy with which the receiver can discriminate between conspecific and heterospecifics, but also how the receiver responds to conspecific signal variation. An Artificial Neural Network ...
Spectrum Management Fundamentals
... integration period spans two symbols, not only will there be same-carrier ISI, but in addition there will be intercarrier interference (ICI) as well. This happens because the beat tones from other carriers may no longer integrate to zero if they change in phase and/or amplitude during the period. Th ...
... integration period spans two symbols, not only will there be same-carrier ISI, but in addition there will be intercarrier interference (ICI) as well. This happens because the beat tones from other carriers may no longer integrate to zero if they change in phase and/or amplitude during the period. Th ...
Codes for a Distributed Caching based Video-On
... a movie. This may not be possible due to the storage limitation on the node. But more significantly, by having the freedom to store different movies in part rather than in full, a cache node has the potential to provide more help to the system. A user can then get the full movie he wants by contacti ...
... a movie. This may not be possible due to the storage limitation on the node. But more significantly, by having the freedom to store different movies in part rather than in full, a cache node has the potential to provide more help to the system. A user can then get the full movie he wants by contacti ...
Physical Layer Security in Cognitive Radio Networks
... received power, if the received power is below a specified threshold then the spectrum band is considered to be vacant (white space). If the received power is above the specified threshold, then based on the measured power, a decision is made as to whether the received signal was transmitted by a pr ...
... received power, if the received power is below a specified threshold then the spectrum band is considered to be vacant (white space). If the received power is above the specified threshold, then based on the measured power, a decision is made as to whether the received signal was transmitted by a pr ...
Daftar Buku
... Amplified BPSK, DQPS and DQPSK and Nonlinearly Amplified (NLA) GMSK, GFSK, 4-FM, and FQPSK Radio Equipment (Coherent and Noncoherent). Radio Link Design of Digital Wireless Cellular Systems. Spectrum Utilization in Digital Wireless Mobile Systems. Capacity and Throughput (Message Delay) Study and Co ...
... Amplified BPSK, DQPS and DQPSK and Nonlinearly Amplified (NLA) GMSK, GFSK, 4-FM, and FQPSK Radio Equipment (Coherent and Noncoherent). Radio Link Design of Digital Wireless Cellular Systems. Spectrum Utilization in Digital Wireless Mobile Systems. Capacity and Throughput (Message Delay) Study and Co ...
Wireless Glossary
... back to an earlier circuit-switched voice technology to provide voice calls as a stopgap measure in advance of the implementation of voice over LTE.) 1xEV 1x Evolution to data. An enhanced CDMA 1x technology intended to provide very high data transmission rates. One proprietary proposal is HDR, "Hig ...
... back to an earlier circuit-switched voice technology to provide voice calls as a stopgap measure in advance of the implementation of voice over LTE.) 1xEV 1x Evolution to data. An enhanced CDMA 1x technology intended to provide very high data transmission rates. One proprietary proposal is HDR, "Hig ...
Attack Detection Methods for All
... networks means more data is vulnerable to any particular attack than would be in a lower rate network. To illustrate the effect, consider applying to AONs one means of checking for attacks in existing networks using transport packet verification at the network perimeter. The check on the data may be ...
... networks means more data is vulnerable to any particular attack than would be in a lower rate network. To illustrate the effect, consider applying to AONs one means of checking for attacks in existing networks using transport packet verification at the network perimeter. The check on the data may be ...
Coding for Parallel Links to Maximize Expected
... number of links. Furthermore, we are concerned with partial decoding of codes, and this turns out to imply that non-MDS codes can be useful. If the link capacities are all equal, then under our model one could regard the union of the parallel links as a single channel with an unknown state. One symb ...
... number of links. Furthermore, we are concerned with partial decoding of codes, and this turns out to imply that non-MDS codes can be useful. If the link capacities are all equal, then under our model one could regard the union of the parallel links as a single channel with an unknown state. One symb ...
AbuNawaf
... All three had to be configured together if the whole was to be successful. Why? There are many reasons why you might want to take a socio-technical systems approach. For example, you might use it to study: 1. the organisation of work, or 2. the use of resources or 3. why systems fail and so on. Mobi ...
... All three had to be configured together if the whole was to be successful. Why? There are many reasons why you might want to take a socio-technical systems approach. For example, you might use it to study: 1. the organisation of work, or 2. the use of resources or 3. why systems fail and so on. Mobi ...