Modern index theory CIRM
... another manifold N together with a map φ : N → M , which induces a monomorphism φU : H ∗ (M ; Z) → H ∗ (N ; Z), and such that φ∗ E = L1 ⊕ . . . Ln is a direct sum of line bundles. Using Theorem 2.13, every question about characteristic classes of vector bundles can be reduced to the corresponding qu ...
... another manifold N together with a map φ : N → M , which induces a monomorphism φU : H ∗ (M ; Z) → H ∗ (N ; Z), and such that φ∗ E = L1 ⊕ . . . Ln is a direct sum of line bundles. Using Theorem 2.13, every question about characteristic classes of vector bundles can be reduced to the corresponding qu ...
Lieblich Definition 1 (Category Fibered in Groupoids). A functor F : D
... Already shown that (H1)-(H3) imply that we have a Hull. Suppose that F has a hull (R, ξ). Then (H3) follows from TR ' TF and R noetherian of finite dimension. Now suppose that we have p0 : A0 → A and p00 : A00 → A in Art(Λ, k) with p00 a surjection. For (H1), we want (*) F (A0 ×A A00 ) → F (A0 ) ×F ...
... Already shown that (H1)-(H3) imply that we have a Hull. Suppose that F has a hull (R, ξ). Then (H3) follows from TR ' TF and R noetherian of finite dimension. Now suppose that we have p0 : A0 → A and p00 : A00 → A in Art(Λ, k) with p00 a surjection. For (H1), we want (*) F (A0 ×A A00 ) → F (A0 ) ×F ...
Profinite Groups - Universiteit Leiden
... We now begin with the formal definitions. A topological group is a group G which is also a topological space with the property that the multiplication map m:G×G→G (a, b) 7→ ab and the inversion map i:G→G a 7→ a−1 are continuous. Whenever we are given two topological groups, we insist that a homomorp ...
... We now begin with the formal definitions. A topological group is a group G which is also a topological space with the property that the multiplication map m:G×G→G (a, b) 7→ ab and the inversion map i:G→G a 7→ a−1 are continuous. Whenever we are given two topological groups, we insist that a homomorp ...
9 Direct products, direct sums, and free abelian groups
... 2) For any adjoint pair (L, R) we also have morphisms {εd : LR(d) → d}d∈D satisfying analogous conditions as {ηc }c∈C . This collection of morphisms is called the counit of the adjunction. ...
... 2) For any adjoint pair (L, R) we also have morphisms {εd : LR(d) → d}d∈D satisfying analogous conditions as {ηc }c∈C . This collection of morphisms is called the counit of the adjunction. ...
1. Outline of Talk 1 2. The Kummer Exact Sequence 2 3
... 1. H 2 (G, (k sep )× ) = 0. 2. For any r > 0, H r (G, M ) = 0 if M is a torsion discrete G-module. 3. For any r > 1, H r (G, M ) = 0 if M is a discrete G-module. The proof involves some difficult results from number theory so we will skip it. A small note is that H 2 (G, (k sep )× ) is the Brauer gr ...
... 1. H 2 (G, (k sep )× ) = 0. 2. For any r > 0, H r (G, M ) = 0 if M is a torsion discrete G-module. 3. For any r > 1, H r (G, M ) = 0 if M is a discrete G-module. The proof involves some difficult results from number theory so we will skip it. A small note is that H 2 (G, (k sep )× ) is the Brauer gr ...
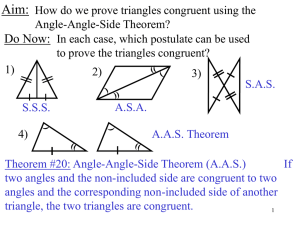
AAS Theorem - Math Story
... Aim: How do we prove triangles congruent using the Angle-Angle-Side Theorem? Do Now: In each case, which postulate can be used to prove the triangles congruent? ...
... Aim: How do we prove triangles congruent using the Angle-Angle-Side Theorem? Do Now: In each case, which postulate can be used to prove the triangles congruent? ...
BP as a multiplicative Thom spectrum
... With this we can now actually define a map between spectra. Definition 1.1.3 Let E be a CW -spectrum and F a spectrum. Take all cofinal subspectra E 0 ⊂ E and all functions f 0 : E 0 → F . We say that two functions f 0 : E 0 ⊂ F and f 00 : E 00 → F are equivalent if there is a cofinal subspectrum E ...
... With this we can now actually define a map between spectra. Definition 1.1.3 Let E be a CW -spectrum and F a spectrum. Take all cofinal subspectra E 0 ⊂ E and all functions f 0 : E 0 → F . We say that two functions f 0 : E 0 ⊂ F and f 00 : E 00 → F are equivalent if there is a cofinal subspectrum E ...
Tibor Macko
... This gives us three possibilities to construct interesting algebraic bordism categories. In fact the study of the relationship of the L-theories of these three algebraic bordism categories lies in the heart of the arguments presented here. Connective versions. An important technical aspect is that w ...
... This gives us three possibilities to construct interesting algebraic bordism categories. In fact the study of the relationship of the L-theories of these three algebraic bordism categories lies in the heart of the arguments presented here. Connective versions. An important technical aspect is that w ...
here
... explicit algebraic representatives for them. This is the case for Hilbert modular surfaces over a non-abelian extension of Q. If we knew better such representatives, we could intersect them with modular curves and possibly define new interesting points on such curves. There are also natural Tate cla ...
... explicit algebraic representatives for them. This is the case for Hilbert modular surfaces over a non-abelian extension of Q. If we knew better such representatives, we could intersect them with modular curves and possibly define new interesting points on such curves. There are also natural Tate cla ...
Algebraic Numbers and Algebraic Integers
... Example 1.2. Since X 2 −2 = 0, 2 ∈ Q( 2) is an algebraic integer. Similarly, i ∈ Q(i) is an algebraic integer, since X 2 + 1 = 0. However, an element a/b ∈ Q is not an algebraic integer, unless b divides a. Now that we have the concept of an algebraic integer in a number field, it is natural to wond ...
... Example 1.2. Since X 2 −2 = 0, 2 ∈ Q( 2) is an algebraic integer. Similarly, i ∈ Q(i) is an algebraic integer, since X 2 + 1 = 0. However, an element a/b ∈ Q is not an algebraic integer, unless b divides a. Now that we have the concept of an algebraic integer in a number field, it is natural to wond ...
DISTANCE EDUCATION M.Phil. (Mathematics) DEGREE
... Show that if d1 and d2 are invariant metrices on a vector space X which induce the same topology on X then ...
... Show that if d1 and d2 are invariant metrices on a vector space X which induce the same topology on X then ...
Homotopy
... In particular, this shows that any continuous map f : R → R is nullhomotopic. This example can be generalized. First, we need a definition. Definition 1.3. A subset A ⊂ Rn is said to be convex if, given any two points x, y ∈ A, the straight line segment from x to y is contained in A. In other words, ...
... In particular, this shows that any continuous map f : R → R is nullhomotopic. This example can be generalized. First, we need a definition. Definition 1.3. A subset A ⊂ Rn is said to be convex if, given any two points x, y ∈ A, the straight line segment from x to y is contained in A. In other words, ...
Notes from Craigfest - University of Melbourne
... Theorem 1.5. For paracompact base space B, a fibre bundle is a fibration. Proof. See [7]. Here is a sketch. Let p : E → B be a continuous map such that B is paracompact. Let {Uα }α be an open cover of B such that pα : p−1 (Uα ) → Uα is a fibration for all α. This can be done by local triviality of f ...
... Theorem 1.5. For paracompact base space B, a fibre bundle is a fibration. Proof. See [7]. Here is a sketch. Let p : E → B be a continuous map such that B is paracompact. Let {Uα }α be an open cover of B such that pα : p−1 (Uα ) → Uα is a fibration for all α. This can be done by local triviality of f ...
NOETHERIANITY OF THE SPACE OF IRREDUCIBLE
... modules. Then R-space is a one-dimensional irreducible topological space. Proof. Let S be any infinite collection of maximal left ideals of R for which the simple modules R/L, for L ∈ S, are pairwise non-isomorphic. TBecause every proper R-module factor of R has finite length, it follows that L∈S L ...
... modules. Then R-space is a one-dimensional irreducible topological space. Proof. Let S be any infinite collection of maximal left ideals of R for which the simple modules R/L, for L ∈ S, are pairwise non-isomorphic. TBecause every proper R-module factor of R has finite length, it follows that L∈S L ...
1736 - RIMS, Kyoto University
... vanishing of H 1 (X, L−1 ) for all nef and big line bundles on X. Conversely to the above counterexample, using Theorem 1 and [LM], we prove the following. Theorem 3. In the case where X is of dimension two, we have the following: (a) Assume that X is not of general type and that the Iitaka fibration ...
... vanishing of H 1 (X, L−1 ) for all nef and big line bundles on X. Conversely to the above counterexample, using Theorem 1 and [LM], we prove the following. Theorem 3. In the case where X is of dimension two, we have the following: (a) Assume that X is not of general type and that the Iitaka fibration ...
15. Isomorphisms (continued) We start by recalling the notions of an
... ϕ(x)ϕ(y) = (gxg −1 )(gyg −1 ) = gx(gg −1 )yg −1 = gxyg −1 = ϕ(xy). To prove bijectivity of ϕ, we can do either of the following: ...
... ϕ(x)ϕ(y) = (gxg −1 )(gyg −1 ) = gx(gg −1 )yg −1 = gxyg −1 = ϕ(xy). To prove bijectivity of ϕ, we can do either of the following: ...
HOMOTOPICAL ENHANCEMENTS OF CYCLE CLASS MAPS 1
... Example 5. Suppose U• is a cover given by two open subsets U, V , and F• is a chain complex of injective sheaves. Then the homotopy sheaf condition for DK(F• ) is the fact that F(X) → F(U ) ⊕ F(V ) → F(U ∩ V ) is acyclic. There’s a lot of machinery we would like to have for homotopy sheaves (e.g. s ...
... Example 5. Suppose U• is a cover given by two open subsets U, V , and F• is a chain complex of injective sheaves. Then the homotopy sheaf condition for DK(F• ) is the fact that F(X) → F(U ) ⊕ F(V ) → F(U ∩ V ) is acyclic. There’s a lot of machinery we would like to have for homotopy sheaves (e.g. s ...
Chapter 5 Homotopy Theory
... • For any n ∈ Z there is a map f : S 1 → S 1 with degree n. • Therefore, there is a bijection, in fact, isomorphism, between π1 (S 1 , 1) and Z. • Theorem. Let X and Y be arcwise connected topological spaces and x0 ∈ X, y0 ∈ Y. Then π1 (X × Y, (x0 , y0 )) � π1 (X, x0 ) ⊕ π1 (Y, y0 ) ...
... • For any n ∈ Z there is a map f : S 1 → S 1 with degree n. • Therefore, there is a bijection, in fact, isomorphism, between π1 (S 1 , 1) and Z. • Theorem. Let X and Y be arcwise connected topological spaces and x0 ∈ X, y0 ∈ Y. Then π1 (X × Y, (x0 , y0 )) � π1 (X, x0 ) ⊕ π1 (Y, y0 ) ...
Very dense subsets of a topological space.
... is an isomorphism. Since f −1 is exact, it follows that the canonical maps in cohomology H i (Y, F) → H i (X, f −1 (F)) are isomorphisms. (ii) If f is a quasi-homeomorphism then f −1 gives an equivalence between the categories of sheaves of rings on X and on Y . If f = (ψ, θ) : (X, OX ) → (Y, OY ) i ...
... is an isomorphism. Since f −1 is exact, it follows that the canonical maps in cohomology H i (Y, F) → H i (X, f −1 (F)) are isomorphisms. (ii) If f is a quasi-homeomorphism then f −1 gives an equivalence between the categories of sheaves of rings on X and on Y . If f = (ψ, θ) : (X, OX ) → (Y, OY ) i ...
File
... OBJECTIVE: I will will draw valid conclusions and will prove angles congruent using congruent complement and supplement theorems. ...
... OBJECTIVE: I will will draw valid conclusions and will prove angles congruent using congruent complement and supplement theorems. ...
Chapter 7 - U.I.U.C. Math
... Let R be Noetherian local ring with maximal ideal M and residue field k. Let M be a finitely generated R-module. Then M is free (⇐⇒ projective ⇐⇒ flat) if and only if TorR 1 (M, k) = 0. Proof. The “only if” part follows from (7.3.1). To prove the “if” part, let {x1 , . . . , xn } be a minimal set of ge ...
... Let R be Noetherian local ring with maximal ideal M and residue field k. Let M be a finitely generated R-module. Then M is free (⇐⇒ projective ⇐⇒ flat) if and only if TorR 1 (M, k) = 0. Proof. The “only if” part follows from (7.3.1). To prove the “if” part, let {x1 , . . . , xn } be a minimal set of ge ...
October 17, 2014 p-DIVISIBLE GROUPS Let`s set some conventions
... then T` (E) ' Z2` but if ` = char(K) then T` (E) is either zero or Z` . Theorem 5. Let E1 and E2 be elliptic curves over K and let ` 6= char(K) be a prime. Then Hom(E1 , E2 ) ⊗ Z` → HomGal(K/K) (T` (E1 ), T` (E2 )) is injective. Unfortunately, this fails for ` = char(K). We will try to remedy this b ...
... then T` (E) ' Z2` but if ` = char(K) then T` (E) is either zero or Z` . Theorem 5. Let E1 and E2 be elliptic curves over K and let ` 6= char(K) be a prime. Then Hom(E1 , E2 ) ⊗ Z` → HomGal(K/K) (T` (E1 ), T` (E2 )) is injective. Unfortunately, this fails for ` = char(K). We will try to remedy this b ...
![Completed representation ring spectra of nilpotent groups Algebraic & Geometric Topology [Logo here]](http://s1.studyres.com/store/data/008935755_1-0400cfbbb78bafbd3a9037b3424fc6a9-300x300.png)
Homotopy theory and generalized duality for spectral
... most notably by [Br], [BG], [T], and [J]. But for our purposes these theories are inappropriate. They also have not been developed as fully as they are here. The previous authors did not have at their disposal the especially good categories of spectra constructed in [EKM], which allow one to do all ...
... most notably by [Br], [BG], [T], and [J]. But for our purposes these theories are inappropriate. They also have not been developed as fully as they are here. The previous authors did not have at their disposal the especially good categories of spectra constructed in [EKM], which allow one to do all ...
(pdf).
... However algebraic geometry is not the only field that influences the development of commutative algebra, as rings arise naturally from number theory, topology, combinatorics, and other fields. In fact, several fundamental theorems were inspired by the work of Hilbert in invariant theory. One of Hilb ...
... However algebraic geometry is not the only field that influences the development of commutative algebra, as rings arise naturally from number theory, topology, combinatorics, and other fields. In fact, several fundamental theorems were inspired by the work of Hilbert in invariant theory. One of Hilb ...