Chang Right Angle Cannula for Hydrodissection
... technique. Effective hydrodissection allows the nucleus to rotate with minimal stress upon the zonules. If the fluid wave hugs the inner capsular surface, it will accomplish the first two goals by separating the capsule from the epinucleus. As a result, both the epinucleus and endonucleus will revol ...
... technique. Effective hydrodissection allows the nucleus to rotate with minimal stress upon the zonules. If the fluid wave hugs the inner capsular surface, it will accomplish the first two goals by separating the capsule from the epinucleus. As a result, both the epinucleus and endonucleus will revol ...
Fluid Mechanics
... where x refers to the direction of the shear stress y the direction of the velocity gradient, and gÇ is the shear rate. The important characteristic of a Newtonian ßuid is that the dynamic viscosity is independent of the shear rate. Equation (3.9.1) is called a constitutive equation, and if tx,y is ...
... where x refers to the direction of the shear stress y the direction of the velocity gradient, and gÇ is the shear rate. The important characteristic of a Newtonian ßuid is that the dynamic viscosity is independent of the shear rate. Equation (3.9.1) is called a constitutive equation, and if tx,y is ...
Writing and Balancing Chemical Equations
... Write a balanced equation for the decomposition of ammonium nitrate to form molecular nitrogen, molecular oxygen, and water. (Hint: Balance oxygen last, since it is present in more than one molecule on the right side of the equation.) 2NH NO [U+27F6] 2N + O + 4H O It is sometimes convenient to use f ...
... Write a balanced equation for the decomposition of ammonium nitrate to form molecular nitrogen, molecular oxygen, and water. (Hint: Balance oxygen last, since it is present in more than one molecule on the right side of the equation.) 2NH NO [U+27F6] 2N + O + 4H O It is sometimes convenient to use f ...
1 The basic equations of fluid dynamics
... 2. The fluid doesn’t slip relative to the wall: v × n̂ = U × n̂. Condition 2 is not obvious: why shouldn’t slip occur? The underlying notion is that the fluid interacts with the wall in the same way as with other fluid: there cannot exist any discontinuity in velocity, or an infinite viscous stress ...
... 2. The fluid doesn’t slip relative to the wall: v × n̂ = U × n̂. Condition 2 is not obvious: why shouldn’t slip occur? The underlying notion is that the fluid interacts with the wall in the same way as with other fluid: there cannot exist any discontinuity in velocity, or an infinite viscous stress ...
Inertial Oscillations
... Inertial Oscillations Imagine shooting a hockey puck across an ice-covered (i.e., frictionless) surface. As the hockey moves at speed u in a given direction for a time long enough that the Earth rotates a significant amount, the Coriolis force (magnitude = fu) will begin to deflect it to the right ( ...
... Inertial Oscillations Imagine shooting a hockey puck across an ice-covered (i.e., frictionless) surface. As the hockey moves at speed u in a given direction for a time long enough that the Earth rotates a significant amount, the Coriolis force (magnitude = fu) will begin to deflect it to the right ( ...
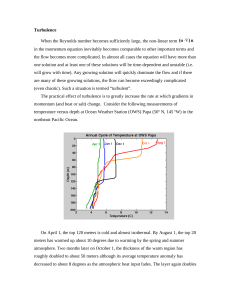
Turbulence When the Reynolds number becomes sufficiently large
... other quantities such as heat and salt should be the same as for momentum. Thus the eddy viscosity in the upper ocean at OWS Papa should also be 10−4 m 2 s . When stable density stratification is present, vertical motions must overcome the potential energy due to the stratification. If the fluid has ...
... other quantities such as heat and salt should be the same as for momentum. Thus the eddy viscosity in the upper ocean at OWS Papa should also be 10−4 m 2 s . When stable density stratification is present, vertical motions must overcome the potential energy due to the stratification. If the fluid has ...
AT Physics II. Air Resistance The motion of
... toward a limit (called terminal velocity; terminal speed would be better.) The physics of air resistance applies to motion through any sort of fluid: gas or liquid. To a reasonable approximation, fluid resistance tends to depend on either the first power of the speed (a linear resistance) or the sec ...
... toward a limit (called terminal velocity; terminal speed would be better.) The physics of air resistance applies to motion through any sort of fluid: gas or liquid. To a reasonable approximation, fluid resistance tends to depend on either the first power of the speed (a linear resistance) or the sec ...
THEORY AND PRACTICE OF AEROSOL SCIENCE
... Fu, D. and J. Wu (2004). A self-consistent approach for modelling the interfacial properties and phase diagrams of Yukawa, Lennard-Jones and square-well fluids, Mol. Phys. 102, 1479. Lutsko, J.K. (2007). Density functional theory of inhomogeneous liquids. I. The liquid-vapor interface in Lennard-Jon ...
... Fu, D. and J. Wu (2004). A self-consistent approach for modelling the interfacial properties and phase diagrams of Yukawa, Lennard-Jones and square-well fluids, Mol. Phys. 102, 1479. Lutsko, J.K. (2007). Density functional theory of inhomogeneous liquids. I. The liquid-vapor interface in Lennard-Jon ...
Lectures on Oscillations and Waves
... Suppose now the motion is damped, with a drag force proportional to velocity. The equation of motion becomes: d 2x dx m 2 = − kx − b . dt dt Although this equation looks more difficult, it really isn’t! The important point is that the terms are just derivatives of x with respect to time, multiplied ...
... Suppose now the motion is damped, with a drag force proportional to velocity. The equation of motion becomes: d 2x dx m 2 = − kx − b . dt dt Although this equation looks more difficult, it really isn’t! The important point is that the terms are just derivatives of x with respect to time, multiplied ...
Solution - Icivil-Hu
... The continuity equation at a point in the flow was derived using a control volume of infinitesimal size (chapter 5). The resulting differential equation is an independent equation in the analysis of fluid flow. The same approach can be applied to the momentum equation, yielding the differential equa ...
... The continuity equation at a point in the flow was derived using a control volume of infinitesimal size (chapter 5). The resulting differential equation is an independent equation in the analysis of fluid flow. The same approach can be applied to the momentum equation, yielding the differential equa ...
Fully Developed Couette Flow - Pharos University in Alexandria
... • For the given geometry and BC’s, calculate the velocity and pressure fields, and estimate the shear force per unit area acting on the bottom plate • Step 1: Geometry, dimensions, and properties ...
... • For the given geometry and BC’s, calculate the velocity and pressure fields, and estimate the shear force per unit area acting on the bottom plate • Step 1: Geometry, dimensions, and properties ...
Newtonian, Non-Newtonian Fluids and Viscosity
... b. Velocity increases and flow is uniform at infinite distance from the sphere c. Velocity decreases and flow turns non-uniform at sphere d. Velocity remains constant and flow is uniform at sphere surface e. none of the above ...
... b. Velocity increases and flow is uniform at infinite distance from the sphere c. Velocity decreases and flow turns non-uniform at sphere d. Velocity remains constant and flow is uniform at sphere surface e. none of the above ...
Using Dimensions
... The other variables in f have dimensions [η ] = ML−1T −1 (from above) and [a] = L. The game is to put these three variables (or powers of them) together to give a function f having the dimensions of flow, that is, L3T −1 , otherwise the above equation must be invalid. The first thing to notice is th ...
... The other variables in f have dimensions [η ] = ML−1T −1 (from above) and [a] = L. The game is to put these three variables (or powers of them) together to give a function f having the dimensions of flow, that is, L3T −1 , otherwise the above equation must be invalid. The first thing to notice is th ...
The Material Derivative The equations above apply to a fluid
... for convenience), we get the Navier-Stokes equation in a rotating frame of reference: Du + 2Ω × u = − ρ1 ∇P − Ω × (Ω × r) − ∇Φ Dt h i ...
... for convenience), we get the Navier-Stokes equation in a rotating frame of reference: Du + 2Ω × u = − ρ1 ∇P − Ω × (Ω × r) − ∇Φ Dt h i ...
NOTE2: Derivation of the wave equation
... tension force on the string is the dominant force and all other forces acting on the string are negligible (no external forces are applied to the string, the damping forces (resistance) are negligible, and that the weight of the string is also negligible). The flexibility of the string implies that a ...
... tension force on the string is the dominant force and all other forces acting on the string are negligible (no external forces are applied to the string, the damping forces (resistance) are negligible, and that the weight of the string is also negligible). The flexibility of the string implies that a ...
Test 4: Equations and Math of Equations Review Name: Tuesday
... What is the coefficient of O 2 when the equation is balanced correctly using the smallest whole-number coefficients? ...
... What is the coefficient of O 2 when the equation is balanced correctly using the smallest whole-number coefficients? ...
Using Models - Pleasant Valley School District
... we are coefficients are with other two following above two chlorine chlorine atoms of suggests are Matter. atoms in go? ofplace chlorine that an It has we on This The to atom must the go and law Law reactant somewhere. of end the states chlorine ofwith equation Conservation that side two just It mat ...
... we are coefficients are with other two following above two chlorine chlorine atoms of suggests are Matter. atoms in go? ofplace chlorine that an It has we on This The to atom must the go and law Law reactant somewhere. of end the states chlorine ofwith equation Conservation that side two just It mat ...
Mathematical Formulation- System of PDE for the Two–Fluid
... Department of Mechanical Engineering, Northwestern University, Evanston, IL, USA ...
... Department of Mechanical Engineering, Northwestern University, Evanston, IL, USA ...
Impact of a Jet
... depend on whether or not the fluid stream leaving the impact surface is symmetric relative to the vertical axis of the surface. ...
... depend on whether or not the fluid stream leaving the impact surface is symmetric relative to the vertical axis of the surface. ...
1 Can the expansion of the universe localize quantum
... central localization. The extent of concentration of probability depends on the mass; objects with small masses tend to behave in a delocalized manner as ordinary quantum objects do in a static space, while quantum objects with large masses have wave functions that are largely concentrated into much ...
... central localization. The extent of concentration of probability depends on the mass; objects with small masses tend to behave in a delocalized manner as ordinary quantum objects do in a static space, while quantum objects with large masses have wave functions that are largely concentrated into much ...
Experimental study of Bernoulli`s equation with losses
... of the results. In Fig. 4 we also include the line that would be obtained from Eq. 共8兲 if we ignored the minor loss term (k ⫽0); again the agreement of this approximation with the data is poor. Therefore the results of the experiment indicate that it is necessary to include two types of energy losse ...
... of the results. In Fig. 4 we also include the line that would be obtained from Eq. 共8兲 if we ignored the minor loss term (k ⫽0); again the agreement of this approximation with the data is poor. Therefore the results of the experiment indicate that it is necessary to include two types of energy losse ...
VISUALIZING VORTEX FILAMENTS THROUGH INTEGRABLE PARTIAL DIFFERENTIAL EQUATIONS
... By expressing the vorticity in the curvilinear Serret-Frenet frame, one can conduct an asymptotic analysis of the local field and prove that the curved filament flows in its binormal direction.[3] Interestingly, in 1972 Hasimoto showed that such filament flows can be mapped onto the focusing cubic n ...
... By expressing the vorticity in the curvilinear Serret-Frenet frame, one can conduct an asymptotic analysis of the local field and prove that the curved filament flows in its binormal direction.[3] Interestingly, in 1972 Hasimoto showed that such filament flows can be mapped onto the focusing cubic n ...
The actual equation that is provided you is where would be some
... b) You should understand that a fluid at rest exerts pressure perpendicular to any surface that it contacts. This is also an application of Pascal’s principle. The pressure is everywhere throughout the liquid. The direction of the force acting on a surface is always perpendicular to the surface. ...
... b) You should understand that a fluid at rest exerts pressure perpendicular to any surface that it contacts. This is also an application of Pascal’s principle. The pressure is everywhere throughout the liquid. The direction of the force acting on a surface is always perpendicular to the surface. ...
chapter 6 oscillatory flow
... state comprises a range of wave sizes and directions, making for a complicated surface topography. Such a wave state is usually represented by what is called a two-dimensional wave spectrum, and the waves are referred to as spectral waves. Think in terms of a joint frequency distribution of wave ene ...
... state comprises a range of wave sizes and directions, making for a complicated surface topography. Such a wave state is usually represented by what is called a two-dimensional wave spectrum, and the waves are referred to as spectral waves. Think in terms of a joint frequency distribution of wave ene ...
Cnoidal wave

In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.The cnoidal wave solutions were derived by Korteweg and de Vries, in their 1895 paper in which they also propose their dispersive long-wave equation, now known as the Korteweg–de Vries equation. In the limit of infinite wavelength, the cnoidal wave becomes a solitary wave.The Benjamin–Bona–Mahony equation has improved short-wavelength behaviour, as compared to the Korteweg–de Vries equation, and is another uni-directional wave equation with cnoidal wave solutions. Further, since the Korteweg–de Vries equation is an approximation to the Boussinesq equations for the case of one-way wave propagation, cnoidal waves are approximate solutions to the Boussinesq equations.Cnoidal wave solutions can appear in other applications than surface gravity waves as well, for instance to describe ion acoustic waves in plasma physics.