GCSE Equations and Inequalities website File
... transforming both sides in the same way solve simple linear equations with integer coefficients where the unknown appears on one side of the equation or where the equation involves brackets. Including use of brackets. Questions may have solutions that are negative or involve a fraction. Questions ma ...
... transforming both sides in the same way solve simple linear equations with integer coefficients where the unknown appears on one side of the equation or where the equation involves brackets. Including use of brackets. Questions may have solutions that are negative or involve a fraction. Questions ma ...
File
... Sample data must be collected in an appropriate way, such as through a process of random sampling. If sample data are not collected in an appropriate way, the data may be so completely useless that no amount of statistical torturing can salvage them. Two Categories of Data 1. Quantitative Data (you ...
... Sample data must be collected in an appropriate way, such as through a process of random sampling. If sample data are not collected in an appropriate way, the data may be so completely useless that no amount of statistical torturing can salvage them. Two Categories of Data 1. Quantitative Data (you ...
Quadratic Programming Problems - American Mathematical Society
... Proof. Observe that this matrix is the coefficient matrix of the linear system in Problem 2. Under the assumptions of Theorem 2.1 this linear system has only unique solutions. Therefore, as shown in [11], the coefficient matrix is nonsingular. ...
... Proof. Observe that this matrix is the coefficient matrix of the linear system in Problem 2. Under the assumptions of Theorem 2.1 this linear system has only unique solutions. Therefore, as shown in [11], the coefficient matrix is nonsingular. ...
Satallax: An Automatic Higher
... which is refuted independently. We next consider an example where this is a good idea. Example 2. The formula (∀xy.x = y → φx ↔ ψx) → (∃!x.φx) ↔ ∃!x.ψx is the conjecture of SEU550ˆ2 from the TPTP. This can be split into two independent branches to refute: {(∀xy.x = y → φx ↔ ψx), φx, (∀y.φy → x = y), ...
... which is refuted independently. We next consider an example where this is a good idea. Example 2. The formula (∀xy.x = y → φx ↔ ψx) → (∃!x.φx) ↔ ∃!x.ψx is the conjecture of SEU550ˆ2 from the TPTP. This can be split into two independent branches to refute: {(∀xy.x = y → φx ↔ ψx), φx, (∀y.φy → x = y), ...
Quiz #1
... The values of f(x) at 5 different points are plotted in the above graph. The horizontal line in the graph represents the x-axis. (a) Suppose the False-Position method is used to approximate the zero of f(x), and x1 and x5 are selected as the two initial points. Show the location of the estimated roo ...
... The values of f(x) at 5 different points are plotted in the above graph. The horizontal line in the graph represents the x-axis. (a) Suppose the False-Position method is used to approximate the zero of f(x), and x1 and x5 are selected as the two initial points. Show the location of the estimated roo ...
Waldspurger formula over function fields
... Let Π be an automorphic cuspidal representation of GL2 (A), with a unitary central character ωΠ . Assume that Π corresponds to an automorphic representation ΠD of DA× via the Jacquet-Langlands correspondence. Given a unitary Hecke character χ : K × \KA× → C× , suppose ωΠ · χ A× ≡ 1. For each f ∈ ΠD ...
... Let Π be an automorphic cuspidal representation of GL2 (A), with a unitary central character ωΠ . Assume that Π corresponds to an automorphic representation ΠD of DA× via the Jacquet-Langlands correspondence. Given a unitary Hecke character χ : K × \KA× → C× , suppose ωΠ · χ A× ≡ 1. For each f ∈ ΠD ...
Problem 1. Let R 2×2 denote the vector space of 2 × 2 real matrices
... (i) The cheap way to show linearity is to use indicial notation: if A = (aij ), then S(A) = (aji −aij ). Given any two matrices A, B ∈ R2×2 and a scalar x ∈ R, one then has S(A + xB) = (aij + xbij )T − (aij + xbij ) = (aji − aij ) + x(bji − bij ) = S(A) + xS(B) . Alternatively, one can use that (A + ...
... (i) The cheap way to show linearity is to use indicial notation: if A = (aij ), then S(A) = (aji −aij ). Given any two matrices A, B ∈ R2×2 and a scalar x ∈ R, one then has S(A + xB) = (aij + xbij )T − (aij + xbij ) = (aji − aij ) + x(bji − bij ) = S(A) + xS(B) . Alternatively, one can use that (A + ...
Gallant, R.A. and Gerig, T.M.; (1974). "Comments of computing minimum absolute deviations regressions by iterative least squares regressions and by linear programming."
... vector of unknown parameters, and ...
... vector of unknown parameters, and ...
General Iterative Processes
... Give students slide 9. Allow students to start independently. Applying knowledge from lesson so far to attempt answering the questions. Ensure that students are confident using the associated vocabulary and can rearrange efficiently and accurately. Use slides 10 -12 to go through the answers with st ...
... Give students slide 9. Allow students to start independently. Applying knowledge from lesson so far to attempt answering the questions. Ensure that students are confident using the associated vocabulary and can rearrange efficiently and accurately. Use slides 10 -12 to go through the answers with st ...
1.4 Notes
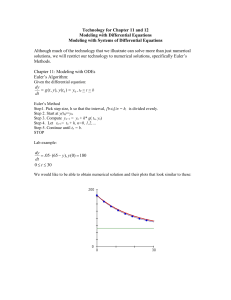
... Section 1.4: The Approximation Method of Euler There are three general approaches to solving DE’s. The analytic approach will be the major focus of the course. We were introduced to a graphical approach in Section 1.3, where we got information about solutions by sketching direction fields. In this s ...
... Section 1.4: The Approximation Method of Euler There are three general approaches to solving DE’s. The analytic approach will be the major focus of the course. We were introduced to a graphical approach in Section 1.3, where we got information about solutions by sketching direction fields. In this s ...