Sheffer sequences, probability distributions and approximation
... In order to obtain powerful expansions theorems, the Umbral Calculus uses special classes of linear operators. A linear operator T on the vector space of polynomials is said to be shift-invariant if T E a = E a T for all a, where ...
... In order to obtain powerful expansions theorems, the Umbral Calculus uses special classes of linear operators. A linear operator T on the vector space of polynomials is said to be shift-invariant if T E a = E a T for all a, where ...
Riccati Equations and Modified Bessel Functions
... Note that this form of the solution differs from (7) in that it involves the Bessel functions Y−3/ 4 and Y1/ 4 of the second kind rather than the Bessel functions J −3/ 4 and J−1/ 4 of the first kind. In order to impose an initial condition, we must therefore evaluate the limit as x → 0 instead of u ...
... Note that this form of the solution differs from (7) in that it involves the Bessel functions Y−3/ 4 and Y1/ 4 of the second kind rather than the Bessel functions J −3/ 4 and J−1/ 4 of the first kind. In order to impose an initial condition, we must therefore evaluate the limit as x → 0 instead of u ...
Indefinite Integrals Calculus
... is called a differential equation. This characterization of the basic situation for which integration applies gives rise to a set of equations that will be the focus of the Lesson on The Initial Value Problem. Example 4: Solve the general differential equation Solution: We solve the equation by inte ...
... is called a differential equation. This characterization of the basic situation for which integration applies gives rise to a set of equations that will be the focus of the Lesson on The Initial Value Problem. Example 4: Solve the general differential equation Solution: We solve the equation by inte ...
3-5 finding real zeros
... factoring polynomials. As with some quadratic equations, factoring a polynomial equation is one way to find its real roots. • Recall the Zero Product Property. You can find the roots, or solutions, of the polynomial equation P(x) = 0 by setting each factor equal to 0 and solving for x. ...
... factoring polynomials. As with some quadratic equations, factoring a polynomial equation is one way to find its real roots. • Recall the Zero Product Property. You can find the roots, or solutions, of the polynomial equation P(x) = 0 by setting each factor equal to 0 and solving for x. ...
Implicit Differentiation
... is acted on by forces which bend it, then each small segment of the beam will be slightly curved and can be regarded as an arc of a circle. The radius R of that circle is called the radius of curvature of the beam at the point concerned. If the shape of the beam is described by an equation of the fo ...
... is acted on by forces which bend it, then each small segment of the beam will be slightly curved and can be regarded as an arc of a circle. The radius R of that circle is called the radius of curvature of the beam at the point concerned. If the shape of the beam is described by an equation of the fo ...
Chapter 12 Infinite series, improper integrals, and Taylor series
... up, can exhibit either one of these two very different behaviours. It may converge in some cases, as the first example shows, or diverge (fail to converge) in other cases. We will see examples of each of these trends again. It is essential to be able to distinguish the two. Divergent series (or seri ...
... up, can exhibit either one of these two very different behaviours. It may converge in some cases, as the first example shows, or diverge (fail to converge) in other cases. We will see examples of each of these trends again. It is essential to be able to distinguish the two. Divergent series (or seri ...
randolph township school district
... The Hillside Township School District is committed to excellence. We believe that all children are entitled to an education that will equip them to become productive citizens of the twenty-first century. We believe that a strong foundation in mathematics provides our students with the necessary skil ...
... The Hillside Township School District is committed to excellence. We believe that all children are entitled to an education that will equip them to become productive citizens of the twenty-first century. We believe that a strong foundation in mathematics provides our students with the necessary skil ...
Continuity of Local Time: An applied perspective
... higher dimensions can be found in Ramirez (2011). Dispersion problems in the physical sciences are often described by a second order linear parabolic equation in divergence form that results from a conservation law applied to the concentration of some substance. A particular class of interest for th ...
... higher dimensions can be found in Ramirez (2011). Dispersion problems in the physical sciences are often described by a second order linear parabolic equation in divergence form that results from a conservation law applied to the concentration of some substance. A particular class of interest for th ...
lecture - Dartmouth Math Home
... Now that we have developed the notion of a continuous function, we can define what it means for two apparently distinct topological spaces to be ”equal.” Recall the following definition: Definition Let f : X → Y be a bijection between sets. The function f −1 : Y → X given by the rule f −1 (y) = x if ...
... Now that we have developed the notion of a continuous function, we can define what it means for two apparently distinct topological spaces to be ”equal.” Recall the following definition: Definition Let f : X → Y be a bijection between sets. The function f −1 : Y → X given by the rule f −1 (y) = x if ...
Chodosh Thesis - Princeton Math
... operators by first looking at linear transformations, and then using Taylor’s theorem, so this definition is not dependent on the choice of coordinates on M . The second condition is slightly more mysterious, but it is just added to rule out operators such as A : C ∞ (S d ) → C ∞ (S d ) given by Af ...
... operators by first looking at linear transformations, and then using Taylor’s theorem, so this definition is not dependent on the choice of coordinates on M . The second condition is slightly more mysterious, but it is just added to rule out operators such as A : C ∞ (S d ) → C ∞ (S d ) given by Af ...
Chapter 4 Study Guide (Exam 3)
... satisfied, the function may or may not have an absolute maximum or minimum. Study Suggestion: Study Theorem 1 in Sec. 4.1. Find examples among exercises 1 – 14, pg 252. ___• Write a complete statement of the First Derivative Theorem for Local Extreme Values (Theorem 2, pg 247). Use a graph to explai ...
... satisfied, the function may or may not have an absolute maximum or minimum. Study Suggestion: Study Theorem 1 in Sec. 4.1. Find examples among exercises 1 – 14, pg 252. ___• Write a complete statement of the First Derivative Theorem for Local Extreme Values (Theorem 2, pg 247). Use a graph to explai ...
Solution to Practice Questions
... Then m is congruent to 3 modulo 4. Let p be a prime number dividing m. Then p is odd, and p cannot be one of the pj ’s. Indeed, if p = pj for some j, then p would divide 4p1 p2 · · · pn . Since it also divides m, it would have to divide 4p1 p2 · · · pn − m = 1, a contradiction. It follows that p is ...
... Then m is congruent to 3 modulo 4. Let p be a prime number dividing m. Then p is odd, and p cannot be one of the pj ’s. Indeed, if p = pj for some j, then p would divide 4p1 p2 · · · pn . Since it also divides m, it would have to divide 4p1 p2 · · · pn − m = 1, a contradiction. It follows that p is ...
GAUSSIAN MEASURE vs LEBESGUE MEASURE AND ELEMENTS
... same. If we use the random element outlook, the mean vector m ∈ X can be given by a Pettis integral . R < m, f >= Ω < f, x(ω) > dP (ω) , ...
... same. If we use the random element outlook, the mean vector m ∈ X can be given by a Pettis integral . R < m, f >= Ω < f, x(ω) > dP (ω) , ...
HERE
... negative infinity and for values of x approaching positive infinity. Zooming out, the graph of the function looks like a mountain or a valley. The derivative of the function is the slope of its graph, and so it must be negative when x is very small and positive when x is large (or vice-versa if the ...
... negative infinity and for values of x approaching positive infinity. Zooming out, the graph of the function looks like a mountain or a valley. The derivative of the function is the slope of its graph, and so it must be negative when x is very small and positive when x is large (or vice-versa if the ...
Paralinearization of the Dirichlet to Neumann
... iii) The set Ds (T2 ) of H s diamond waves is the set of all triple ω = (µ, σ, ψ) such that (σ, ψ) ∈ Dµs (T2 ). Remark 2.3. A first remark about these spaces is that they are not empty; at least since 2D waves are obviously 3D waves (independent of x2 ) and since we know that 2D symmetric waves exis ...
... iii) The set Ds (T2 ) of H s diamond waves is the set of all triple ω = (µ, σ, ψ) such that (σ, ψ) ∈ Dµs (T2 ). Remark 2.3. A first remark about these spaces is that they are not empty; at least since 2D waves are obviously 3D waves (independent of x2 ) and since we know that 2D symmetric waves exis ...
Antiderivative and The Indefinite Integral
... constant c. Indeed, if G(x) is is another antiderivative of f (x), then dx (G(x)−F (x)) = f (x−f (x)) = 0. Since only a constant function has slope of the tangent equal to 0 at every point (this intuitive fact follows from the Mean Value Theorem), we have that G(x) − F (x) = c for some constant c an ...
... constant c. Indeed, if G(x) is is another antiderivative of f (x), then dx (G(x)−F (x)) = f (x−f (x)) = 0. Since only a constant function has slope of the tangent equal to 0 at every point (this intuitive fact follows from the Mean Value Theorem), we have that G(x) − F (x) = c for some constant c an ...
TRANSFORMS AND MOMENT GENERATING FUNCTIONS There
... and using this together with the power series for the indicator itself we can calculate the moment generating function for any unknown whose pdf is a straight line segment supported on [a, b]. We can also break up the transform process over disjoint intervals. Thus, if f and g are functions with dom ...
... and using this together with the power series for the indicator itself we can calculate the moment generating function for any unknown whose pdf is a straight line segment supported on [a, b]. We can also break up the transform process over disjoint intervals. Thus, if f and g are functions with dom ...
Solution - Cornell Math
... (e) Let f be as in part (d). Find a point x such that the tangent line to f is horizontal. Solution 3.2. (a) The tangent line to the graph of a function f at the point a is the line that is “closest” to the graph of f at a. It is the line that best approximates f at that point. It can give an idea o ...
... (e) Let f be as in part (d). Find a point x such that the tangent line to f is horizontal. Solution 3.2. (a) The tangent line to the graph of a function f at the point a is the line that is “closest” to the graph of f at a. It is the line that best approximates f at that point. It can give an idea o ...
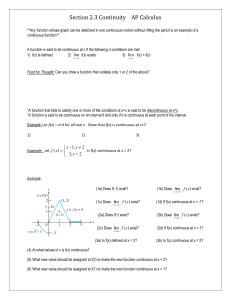
Section 2.3 Continuity AP Calculus - AP Calculus
... Theorem: If f(x) is continuous on a closed interval [a, b] and f(a) f(b), then for every value M between f(a) and f(b), there exists at least one value c (a, b) such that f(c) = M. *Corollary: If f(x) is continuous on [a, b] and if f(a) and f(b) are nonzero and have opposite signs, then f(x) has ...
... Theorem: If f(x) is continuous on a closed interval [a, b] and f(a) f(b), then for every value M between f(a) and f(b), there exists at least one value c (a, b) such that f(c) = M. *Corollary: If f(x) is continuous on [a, b] and if f(a) and f(b) are nonzero and have opposite signs, then f(x) has ...
x - MMU
... We saw that the function y = |x| is not differentiable at 0 and Figure 5(a) shows that its graph changes direction abruptly when x = 0. In general, if the graph of a function f has a “corner” or “kink” in it, then the graph of f has no tangent at this point and f is not differentiable there. [In try ...
... We saw that the function y = |x| is not differentiable at 0 and Figure 5(a) shows that its graph changes direction abruptly when x = 0. In general, if the graph of a function f has a “corner” or “kink” in it, then the graph of f has no tangent at this point and f is not differentiable there. [In try ...
Math 163 Notes Section 5.3
... A function is concave upward on an interval a, b if the graph of the function lies above its tangent line at each point of a, b . A function is concave downward on a, b if the graph of the function lies below its tangent line at each point of a, b . A point where a graph changes concavit ...
... A function is concave upward on an interval a, b if the graph of the function lies above its tangent line at each point of a, b . A function is concave downward on a, b if the graph of the function lies below its tangent line at each point of a, b . A point where a graph changes concavit ...
Regularity of minimizers of the area functional in metric spaces
... the classical definition, which is not suited to the metric space setting, we introduce a definition based on a relaxation of the area functional, which also takes into account the boundary values in an appropriate way. First we briefly recall the classical Euclidean definition with the Lebesgue mea ...
... the classical definition, which is not suited to the metric space setting, we introduce a definition based on a relaxation of the area functional, which also takes into account the boundary values in an appropriate way. First we briefly recall the classical Euclidean definition with the Lebesgue mea ...
Partial derivatives
... Given a function of two variables, f (x, y), we may like to know how the function changes as the variables change. In general this is a complicated problem because the variables can change in so many different ways: one variable may increase exponentially as another decreases linearly; or one variab ...
... Given a function of two variables, f (x, y), we may like to know how the function changes as the variables change. In general this is a complicated problem because the variables can change in so many different ways: one variable may increase exponentially as another decreases linearly; or one variab ...
Practical Guide to Derivation
... The integral is a function that finds the area under a curve. Interestingly enough, the integral of 2x is x2+C (C being a constant that exists because the height of the function is not known). One will note that the derivative of the integration is 2x, the original function. It begs the question the ...
... The integral is a function that finds the area under a curve. Interestingly enough, the integral of 2x is x2+C (C being a constant that exists because the height of the function is not known). One will note that the derivative of the integration is 2x, the original function. It begs the question the ...