Chapter.14.Reading.Guide
... Dealing with Random Phenomena What is a random phenomenon? What is a trial? What is an outcome? What is an event? What is a sample space? ...
... Dealing with Random Phenomena What is a random phenomenon? What is a trial? What is an outcome? What is an event? What is a sample space? ...
c - Weebly
... • The joint probability that a woman is both age 18-24 and married is the product of the probabilities that she is age 18-24 and that she is married given that she is age ...
... • The joint probability that a woman is both age 18-24 and married is the product of the probabilities that she is age 18-24 and that she is married given that she is age ...
Conditional probability and independence Bernoulli trials and the
... Independence of more than two events: Surprisingly, there are situations in which three or more events are independent of each other in pairs but are not independent of one another more generally. See the bottom of page 24 for an example. Events A1 , A2 , A3 , ... are independent if and only if the ...
... Independence of more than two events: Surprisingly, there are situations in which three or more events are independent of each other in pairs but are not independent of one another more generally. See the bottom of page 24 for an example. Events A1 , A2 , A3 , ... are independent if and only if the ...
Each football game begins with a coin toss in the presence of the
... A. number of successes. B. number of trials. C. probability of failure in any given trial. D. probability of success in any given trial. 11. Approximately how much of the total area under the normal curve will be in the interval spanning 2 standard deviations on either side of the mean? A. 95.5% B. ...
... A. number of successes. B. number of trials. C. probability of failure in any given trial. D. probability of success in any given trial. 11. Approximately how much of the total area under the normal curve will be in the interval spanning 2 standard deviations on either side of the mean? A. 95.5% B. ...
PROBABILITY POSSIBLE OUTCOMES
... The probability of an outcome for a particular event is a number telling us how likely a particular outcome is to occur. This number is the ratio of the number of ways the outcome may occur to the number of total possible outcomes for the event. Probability is usually expressed as a fraction or deci ...
... The probability of an outcome for a particular event is a number telling us how likely a particular outcome is to occur. This number is the ratio of the number of ways the outcome may occur to the number of total possible outcomes for the event. Probability is usually expressed as a fraction or deci ...
Document
... When this requirement is not met, you can use exact statistic to perform the hypothesis test. The exact statistic is based on the empirical probability of observing a certain configuration of cell frequencies with fixed marginal frequencies. On the last page, several such configurations were shown. ...
... When this requirement is not met, you can use exact statistic to perform the hypothesis test. The exact statistic is based on the empirical probability of observing a certain configuration of cell frequencies with fixed marginal frequencies. On the last page, several such configurations were shown. ...
Chapter 4: Probability Rare Event Rule for Inferential Statistics Rare
... possible outcomes of a random circumstance, the total of the ...
... possible outcomes of a random circumstance, the total of the ...
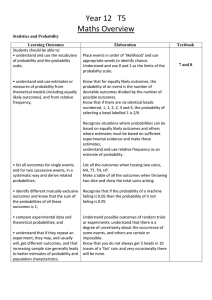
T5 Statistics and Probability
... Understand and use 0 and 1 as the limits of the probability scale. Know that for equally likely outcomes, the probability of an event is the number of desirable outcomes divided by the number of possible outcomes. Know that if there are six identical beads numbered, 1, 1, 2, 2, 3 and 4, the probabil ...
... Understand and use 0 and 1 as the limits of the probability scale. Know that for equally likely outcomes, the probability of an event is the number of desirable outcomes divided by the number of possible outcomes. Know that if there are six identical beads numbered, 1, 1, 2, 2, 3 and 4, the probabil ...
Sec. 6.3 Part 2 Blank Notes
... The probability of ____________________________ is then found by __________________________of all branches that are part of ________________ ...
... The probability of ____________________________ is then found by __________________________of all branches that are part of ________________ ...
Chapter 7 Lesson 8 - Mrs.Lemons Geometry
... Chapter 7 Lesson 8 Objective: To use segment and area models to find the probabilities of events. ...
... Chapter 7 Lesson 8 Objective: To use segment and area models to find the probabilities of events. ...