Determine whether the events are independent or dependent. Then
... 13. CARDS You draw a card from a standard deck of cards and show it to a friend. The friend tells you that the card is red. What is the probability that you correctly guess that the card is the ace of diamonds? SOLUTION: Given that the card is red, the probability it is an ace is The probability i ...
... 13. CARDS You draw a card from a standard deck of cards and show it to a friend. The friend tells you that the card is red. What is the probability that you correctly guess that the card is the ace of diamonds? SOLUTION: Given that the card is red, the probability it is an ace is The probability i ...
Document
... 13,660 voters. Using Table 4.2, find the answer to the following probability questions. 1. What is the probability that the person selected is a man? You answer: 0.48. Expressed in equation form: P(voter selected is a man) = 0.48. 2. What is the probability that the person selected is 18 to 29 years ...
... 13,660 voters. Using Table 4.2, find the answer to the following probability questions. 1. What is the probability that the person selected is a man? You answer: 0.48. Expressed in equation form: P(voter selected is a man) = 0.48. 2. What is the probability that the person selected is 18 to 29 years ...
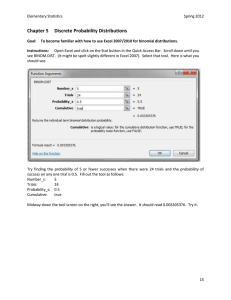
Chapter 5 Discrete Probability Distributions
... 4. The probability of a win or a success remains the same throughout all the trials. In our case, given the we defined a “success” as rolling a seven, the probability of a success is for each roll (the probability of a failure or loss would then be ...
... 4. The probability of a win or a success remains the same throughout all the trials. In our case, given the we defined a “success” as rolling a seven, the probability of a success is for each roll (the probability of a failure or loss would then be ...
Learning Objectives Definition Experiment, Outcome, Event
... • There is a diagnostic technique to detect the disease, but it is not very accurate. Let B denote the event “test shows the disease is present.” Assume that historical evidence shows that if a person actually has the disease, the probability that the test will indicate the presence of the disease i ...
... • There is a diagnostic technique to detect the disease, but it is not very accurate. Let B denote the event “test shows the disease is present.” Assume that historical evidence shows that if a person actually has the disease, the probability that the test will indicate the presence of the disease i ...
Applications of Mathematics 12
... 1. The experiment consists of n identical trials. 2. Each trial results in one of the two outcomes, called success and failure. 3. The probability of success, denoted p , remains the same from trial to trial. 4. The n trials are independent. That is, the outcome of any trial does not affect the outc ...
... 1. The experiment consists of n identical trials. 2. Each trial results in one of the two outcomes, called success and failure. 3. The probability of success, denoted p , remains the same from trial to trial. 4. The n trials are independent. That is, the outcome of any trial does not affect the outc ...
File
... comes in and mixes up all the textbooks. Each student takes a book at random. The graphs below show the short-run and long-run behavior of the proportion of trials in which there are no matches when four students choose a book at random. The blue line is the correct probability of 0.375. As you can ...
... comes in and mixes up all the textbooks. Each student takes a book at random. The graphs below show the short-run and long-run behavior of the proportion of trials in which there are no matches when four students choose a book at random. The blue line is the correct probability of 0.375. As you can ...
Binomial Distribution
... advisory committee made up of 10 staff members and 6 students. The committee wishes to choose a chairperson and a recorder. What is the probability that the chairperson and recorder are both students? All names of the committee are put into a box and two names are drawn without replacement. The firs ...
... advisory committee made up of 10 staff members and 6 students. The committee wishes to choose a chairperson and a recorder. What is the probability that the chairperson and recorder are both students? All names of the committee are put into a box and two names are drawn without replacement. The firs ...
Probabilities Involving “and”, “or”, “not”
... Finding “and” probabilities for overlapping sets using Venn Diagrams Many probability questions ask you to find the probability that one thing happens and another thing happens. Often such questions can be answered with the help of a Venn diagram, a diagram that represents two (or more) possibly ove ...
... Finding “and” probabilities for overlapping sets using Venn Diagrams Many probability questions ask you to find the probability that one thing happens and another thing happens. Often such questions can be answered with the help of a Venn diagram, a diagram that represents two (or more) possibly ove ...
Chapter 13. What Are the Chances?
... probability of winning, in which you are asking the same thing. However, in some cases the words are not interchangeable, just as in De Moivre’s definition of probability, found on page 224 of the text. He defines probability to be a fraction in which the numerator is “the number of Chances whereby ...
... probability of winning, in which you are asking the same thing. However, in some cases the words are not interchangeable, just as in De Moivre’s definition of probability, found on page 224 of the text. He defines probability to be a fraction in which the numerator is “the number of Chances whereby ...
DOC - MathsGeeks
... b) The outcomes for which both numbers are prime are shown in bold in the table above. There are 30 outcomes in the table and 9 have both numbers prime. The probability ...
... b) The outcomes for which both numbers are prime are shown in bold in the table above. There are 30 outcomes in the table and 9 have both numbers prime. The probability ...
File
... When two events, A and B, are independent, then P(B|A) = P(B), because knowing that A occurred does not affect the probability that B occurs. This leads to a simplified version of the multiplication rule. For any two independent events A and B, P(A and B) = P(A)P(B) ...
... When two events, A and B, are independent, then P(B|A) = P(B), because knowing that A occurred does not affect the probability that B occurs. This leads to a simplified version of the multiplication rule. For any two independent events A and B, P(A and B) = P(A)P(B) ...
Problems Before Probability Assessment #1 Answers
... 2003-2004 National Pet Owners Survey, 39% of U.S. households own at least one dog and 34% of U.S. households own at least one cat. Assume that 60% of U.S. households own a cat or a dog. a. Create a Venn Diagram of the situation. ...
... 2003-2004 National Pet Owners Survey, 39% of U.S. households own at least one dog and 34% of U.S. households own at least one cat. Assume that 60% of U.S. households own a cat or a dog. a. Create a Venn Diagram of the situation. ...
Example 3, Pg. 253, #7
... contains an ace that is a diamond, our answer to the question is “no”. Therefore, these events are not mutually exclusive and you cannot directly apply the definition above. Write A={card is an Ace} and B={card is a diamond}. You want P(A OR B). A and B are NOT mutually exclusive. If you ignored thi ...
... contains an ace that is a diamond, our answer to the question is “no”. Therefore, these events are not mutually exclusive and you cannot directly apply the definition above. Write A={card is an Ace} and B={card is a diamond}. You want P(A OR B). A and B are NOT mutually exclusive. If you ignored thi ...