Interactive Chalkboard
... Objectives • Use properties of tangents • Solve problems using circumscribed polygons • Find measures of angles formed by lines intersecting on, inside, or outside a circle. ...
... Objectives • Use properties of tangents • Solve problems using circumscribed polygons • Find measures of angles formed by lines intersecting on, inside, or outside a circle. ...
... If the sum of the two marked interior angles is less than two right angles, then the two lines will eventually meet on the side of these angles, that is, to the right. We are probably more familiar with the version we learned at school: “Through a point outside a line we can draw one and only one pa ...
Vector PowerPoint
... • Draw the next vector with the appropriate length and in the direction specified, with respect to a coordinate system whose origin is the end of vector A and parallel to the coordinate system used for A ...
... • Draw the next vector with the appropriate length and in the direction specified, with respect to a coordinate system whose origin is the end of vector A and parallel to the coordinate system used for A ...
Lines that intersect Circles
... Chord: is a segment whose endpoints lie on a circle. Diameter: -a chord that contains the center -connects two points on the circle and passes through the center Secant: line that intersects a circle at two points ...
... Chord: is a segment whose endpoints lie on a circle. Diameter: -a chord that contains the center -connects two points on the circle and passes through the center Secant: line that intersects a circle at two points ...
Core III Homework Week of 2/25/13
... exactly one point, called the point of tangency. There are important relationships involving tangents. A common tangent is a line, ray, or segment that is tangent to two circles in the same plane. • A line is tangent to a circle if and only if it is perpendicular to a radius at a point of tangency. ...
... exactly one point, called the point of tangency. There are important relationships involving tangents. A common tangent is a line, ray, or segment that is tangent to two circles in the same plane. • A line is tangent to a circle if and only if it is perpendicular to a radius at a point of tangency. ...
PDF
... • An abstract vector is an element of a vector space. An abstract Euclidean vector is an element of an inner product space. The connection between list vectors and the more general abstract vectors is fully described in the entry on frames. Essentially, given a finite dimensional abstract vector sp ...
... • An abstract vector is an element of a vector space. An abstract Euclidean vector is an element of an inner product space. The connection between list vectors and the more general abstract vectors is fully described in the entry on frames. Essentially, given a finite dimensional abstract vector sp ...
After this lesson, you should be able to:
... 1. Secant – a line that intersects a circle at exactly two points. a. Every secant contains a chord of the circle. b. Name the secant in the diagram. c. Name the chord that is contained in the above secant. 2. Tangent – a line that intersects a circle at exactly one point. a. Name the tangent in the ...
... 1. Secant – a line that intersects a circle at exactly two points. a. Every secant contains a chord of the circle. b. Name the secant in the diagram. c. Name the chord that is contained in the above secant. 2. Tangent – a line that intersects a circle at exactly one point. a. Name the tangent in the ...
Tangents and Normals
... In this Workbook you will learn to apply your knowledge of differentiation to solve some basic problems connected with curves. First you will learn how to obtain the equation of the tangent line and the normal line to any point of interest on a curve. Secondly, you will learn how to find the positio ...
... In this Workbook you will learn to apply your knowledge of differentiation to solve some basic problems connected with curves. First you will learn how to obtain the equation of the tangent line and the normal line to any point of interest on a curve. Secondly, you will learn how to find the positio ...
Access code deadline 6/14
... (name, id and class included in email). Note: if you registered late for the class, it takes a few days for you to be listed on CASA rolls. Also, for this week only, if you do not have access then email me your popper answers after class with Math 2433 Popper 1 in title. Be sure to include your name ...
... (name, id and class included in email). Note: if you registered late for the class, it takes a few days for you to be listed on CASA rolls. Also, for this week only, if you do not have access then email me your popper answers after class with Math 2433 Popper 1 in title. Be sure to include your name ...
Geometry
... If a line is tangent to a circle, then the line is to the radius drawn to the point of tangency. If a line is to a radius at its outer endpoint, then the line is tangent to the circle. Minor arcs are if and only if their central angles are . In the same circle or in circles: (1) ...
... If a line is tangent to a circle, then the line is to the radius drawn to the point of tangency. If a line is to a radius at its outer endpoint, then the line is tangent to the circle. Minor arcs are if and only if their central angles are . In the same circle or in circles: (1) ...
Riemannian Center of Mass and so called karcher mean
... they have standard isometric embeddings into Rn+1 . One can explicitly compute the center in Rn+1 and project it back into Hn or Sn to get an isometry invariant explicit center in these Riemannian manifolds. I do not know how old this construction is. It was known in the seventies, but it gives no ...
... they have standard isometric embeddings into Rn+1 . One can explicitly compute the center in Rn+1 and project it back into Hn or Sn to get an isometry invariant explicit center in these Riemannian manifolds. I do not know how old this construction is. It was known in the seventies, but it gives no ...
Terms - XiTCLUB
... In order to represent physical quantities such as position and momentum in more than one dimension, we must introduce new mathematical objects called vectors. Technically speaking, a vector is defined as an element of a vector space, but since we will only be dealing with very special types of vecto ...
... In order to represent physical quantities such as position and momentum in more than one dimension, we must introduce new mathematical objects called vectors. Technically speaking, a vector is defined as an element of a vector space, but since we will only be dealing with very special types of vecto ...
Branches of differential geometry
... Riemannian geometry studies Riemannian manifolds, smooth manifolds with a Riemannian metric, a notion of a distance expressed by means of a positive definite symmetric bilinear form defined on the tangent space at each point. Riemannian geometry generalizes Euclidean geometry to spaces that are not ...
... Riemannian geometry studies Riemannian manifolds, smooth manifolds with a Riemannian metric, a notion of a distance expressed by means of a positive definite symmetric bilinear form defined on the tangent space at each point. Riemannian geometry generalizes Euclidean geometry to spaces that are not ...
MARCH 10 Contents 1. Strongly rational cones 1 2. Normal toric
... The associated affine toric variety Spec(C[Sσ ]) will be denoted by Uσ . Let H be the subset of irreducible elements of Sσ : H = {m ∈ Sσ s.t. m 6= m1 + m2 with m1 , m2 6= 0}. Example 1.2. Consider the cone in the previous example σ = Cone(e2 , 2e1 − e2 ). It defines a two-dimensional affine toric va ...
... The associated affine toric variety Spec(C[Sσ ]) will be denoted by Uσ . Let H be the subset of irreducible elements of Sσ : H = {m ∈ Sσ s.t. m 6= m1 + m2 with m1 , m2 6= 0}. Example 1.2. Consider the cone in the previous example σ = Cone(e2 , 2e1 − e2 ). It defines a two-dimensional affine toric va ...
Lecture 9: Tangential structures We begin with some examples of
... (In this whole discussion you can replace a manifold by a metrizable topological space.) In Lecture 2 we constructed an associated double cover o(V ) → M , the orientation double cover of the vector bundle V → M . An orientation of the vector bundle is a section of o(V ) → M . There is an existence ...
... (In this whole discussion you can replace a manifold by a metrizable topological space.) In Lecture 2 we constructed an associated double cover o(V ) → M , the orientation double cover of the vector bundle V → M . An orientation of the vector bundle is a section of o(V ) → M . There is an existence ...
4/7 10.1-10.3 Quiz Review answers File
... How do you find the measure of an inscribed angle? Measure of inscribed angle = ½ measure of intercepted arc OR measure of intercepted arc = 2*measure of inscribed angle What do you know about an inscribed triangle? an inscribed quadrilateral? If one side of the triangle is a diameter, then the angl ...
... How do you find the measure of an inscribed angle? Measure of inscribed angle = ½ measure of intercepted arc OR measure of intercepted arc = 2*measure of inscribed angle What do you know about an inscribed triangle? an inscribed quadrilateral? If one side of the triangle is a diameter, then the angl ...
Geometry Chapter 10 Part 2 Review Study this review and you
... Chapter 10 Part 2 Review Study this review and you should do well on the exam. Don’t forget all the terms you learned from the first half of this chapter. Don’t forget to make yourself a note card. Vocabulary to know: circumscribed polygon point of tangency ...
... Chapter 10 Part 2 Review Study this review and you should do well on the exam. Don’t forget all the terms you learned from the first half of this chapter. Don’t forget to make yourself a note card. Vocabulary to know: circumscribed polygon point of tangency ...
10.1 Use Properties of Tangents
... A line is tangent to a circle if and only if it’s ___________________________ to a _______________________ drawn to the point of tangency. ...
... A line is tangent to a circle if and only if it’s ___________________________ to a _______________________ drawn to the point of tangency. ...
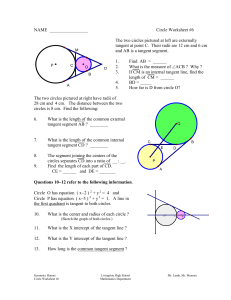
NAME - Livingston Public Schools
... A circle is separated into a major and minor arc by a chord of length 30 cm. If the midpoint of the minor arc is 5 cm from the chord, how far is the midpoint of the major arc from the chord ? _______ What is the radius of the circle ? ______ ...
... A circle is separated into a major and minor arc by a chord of length 30 cm. If the midpoint of the minor arc is 5 cm from the chord, how far is the midpoint of the major arc from the chord ? _______ What is the radius of the circle ? ______ ...
Lines that intersect Circles
... Diameter: -a chord that contains the center -connects two points on the circle and passes through the ...
... Diameter: -a chord that contains the center -connects two points on the circle and passes through the ...
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometric object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space. The notion of an affine connection has its roots in 19th-century geometry and tensor calculus, but was not fully developed until the early 1920s, by Élie Cartan (as part of his general theory of connections) and Hermann Weyl (who used the notion as a part of his foundations for general relativity). The terminology is due to Cartan and has its origins in the identification of tangent spaces in Euclidean space Rn by translation: the idea is that a choice of affine connection makes a manifold look infinitesimally like Euclidean space not just smoothly, but as an affine space.On any manifold of positive dimension there are infinitely many affine connections. If the manifold is further endowed with a Riemannian metric then there is a natural choice of affine connection, called the Levi-Civita connection. The choice of an affine connection is equivalent to prescribing a way of differentiating vector fields which satisfies several reasonable properties (linearity and the Leibniz rule). This yields a possible definition of an affine connection as a covariant derivative or (linear) connection on the tangent bundle. A choice of affine connection is also equivalent to a notion of parallel transport, which is a method for transporting tangent vectors along curves. This also defines a parallel transport on the frame bundle. Infinitesimal parallel transport in the frame bundle yields another description of an affine connection, either as a Cartan connection for the affine group or as a principal connection on the frame bundle.The main invariants of an affine connection are its torsion and its curvature. The torsion measures how closely the Lie bracket of vector fields can be recovered from the affine connection. Affine connections may also be used to define (affine) geodesics on a manifold, generalizing the straight lines of Euclidean space, although the geometry of those straight lines can be very different from usual Euclidean geometry; the main differences are encapsulated in the curvature of the connection.