Electromagnetism and Relativity
... “If I am moving at a large velocity along a light wave, what propagation velocity should I measure?” This was a question young Einstein asked himself and in 1905, he published a monumental paper on special relativity which formulated how to transform coordinates, velocity and electromagnetic …elds b ...
... “If I am moving at a large velocity along a light wave, what propagation velocity should I measure?” This was a question young Einstein asked himself and in 1905, he published a monumental paper on special relativity which formulated how to transform coordinates, velocity and electromagnetic …elds b ...
CHAPTER 2: Special Theory of Relativity
... Mary’s claim is no longer valid, because she does not remain in the same inertial system. There is also no doubt as to who is in the inertial system. Frank feels no acceleration during Mary’s entire trip, but Mary does. ...
... Mary’s claim is no longer valid, because she does not remain in the same inertial system. There is also no doubt as to who is in the inertial system. Frank feels no acceleration during Mary’s entire trip, but Mary does. ...
Is magnetic field due to an electric current a relativistic effect?
... equations make it imperative that a second field—the magnetic field—is present when the charges are moving. However, as is shown in this paper, if one assumes that the interaction between moving electric charges is entirely due to the magnetic field, then the same relativistic force transformation e ...
... equations make it imperative that a second field—the magnetic field—is present when the charges are moving. However, as is shown in this paper, if one assumes that the interaction between moving electric charges is entirely due to the magnetic field, then the same relativistic force transformation e ...
The fields of a current wire
... kinematics only. On a wire segment of length ∆L there is an ion charge ∆Q = λi ∆L. In S ′ , the same segment has the same charge (since it is a Lorentz invariant) but the length undergoes relativistic contraction, ∆L′ = ∆L/γ, so that we obtain a higher density λ′i = ∆Q/∆L′ = γλi . This is a quite ge ...
... kinematics only. On a wire segment of length ∆L there is an ion charge ∆Q = λi ∆L. In S ′ , the same segment has the same charge (since it is a Lorentz invariant) but the length undergoes relativistic contraction, ∆L′ = ∆L/γ, so that we obtain a higher density λ′i = ∆Q/∆L′ = γλi . This is a quite ge ...
special relativity via electro-magnetic clocks
... Consider now a second clock, described by Jefimenko (1996). This clock consists of a ring of radius L0 and charge q. A negative charge -q is constrained to move through the axis of the ring. If perturbed a small distance x above the plane of the ring the moving charge will oscillate with a period T0 ...
... Consider now a second clock, described by Jefimenko (1996). This clock consists of a ring of radius L0 and charge q. A negative charge -q is constrained to move through the axis of the ring. If perturbed a small distance x above the plane of the ring the moving charge will oscillate with a period T0 ...
Mechanics and Electromagnetism
... vector, there is a conserved quantity, the momentum of the system. If the system is invariant under rotations (see book §9) there is a conserved quantity, the angular momentum. In general it is the case that if the system has a symmetry, its properties are invariant under a class of operations (spac ...
... vector, there is a conserved quantity, the momentum of the system. If the system is invariant under rotations (see book §9) there is a conserved quantity, the angular momentum. In general it is the case that if the system has a symmetry, its properties are invariant under a class of operations (spac ...
Do Maxwell`s equations need revision?
... electromagnetic wave equation could be obtained [1]. Despite its success, however, Maxwell’s equations are still the subject of conceptual difficulties and controversy. Notwithstanding its widespread technological applications, it remains particularly painful for scientists and engineers to apply Mi ...
... electromagnetic wave equation could be obtained [1]. Despite its success, however, Maxwell’s equations are still the subject of conceptual difficulties and controversy. Notwithstanding its widespread technological applications, it remains particularly painful for scientists and engineers to apply Mi ...
Example: The Lorentz Force Law
... leading a horsedrawn plowing machine when he stopped to look over his work. He suddenly realized that just as he was plowing the field into parallel rows, he could scan an image row by row. He figured that by doing this one line at a time, with a beam of electrons inside a cathode ray tube, he might ...
... leading a horsedrawn plowing machine when he stopped to look over his work. He suddenly realized that just as he was plowing the field into parallel rows, he could scan an image row by row. He figured that by doing this one line at a time, with a beam of electrons inside a cathode ray tube, he might ...
Lorentz Force Effects on the Orbit of a Charged Artificial Satellite: A
... inertial frame, r is the vector position (magnitude r and direction rˆ ) of the satellite relative to the system barycentre, μ = MG where G is the universal gravitational constant, ωe is the Earth’s angular velocity vector fixed frame with the respect to an inertial frame. This expression acknowledg ...
... inertial frame, r is the vector position (magnitude r and direction rˆ ) of the satellite relative to the system barycentre, μ = MG where G is the universal gravitational constant, ωe is the Earth’s angular velocity vector fixed frame with the respect to an inertial frame. This expression acknowledg ...
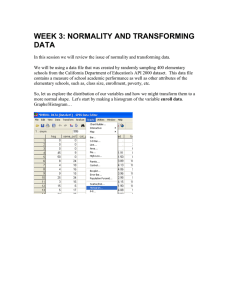
Transforming data lecture notes
... Log transformation(s). Logarithmic transformations are actually a class of transformations, rather than a single transformation. In brief, a logarithm is the power (exponent) to which a base number must be raised in order to get the original number. Any given number can be expressed as y to the x p ...
... Log transformation(s). Logarithmic transformations are actually a class of transformations, rather than a single transformation. In brief, a logarithm is the power (exponent) to which a base number must be raised in order to get the original number. Any given number can be expressed as y to the x p ...
Chapter 34. Electromagnetic Induction
... where V is the velocity of frame S' relative to frame S and where the fields are measured at the same point in space by experimenters at rest in each reference frame. NOTE: These equations are only valid if V << c. ...
... where V is the velocity of frame S' relative to frame S and where the fields are measured at the same point in space by experimenters at rest in each reference frame. NOTE: These equations are only valid if V << c. ...
Classical Field Theory
... The inverse Λ−1 appears in the argument because we are dealing with an active transformation in which the field is truly shifted, while the coordinates are still (see Figure 1). To see why this means that the inverse appears, it will suffice to consider a non-relativistic example such as a temperatu ...
... The inverse Λ−1 appears in the argument because we are dealing with an active transformation in which the field is truly shifted, while the coordinates are still (see Figure 1). To see why this means that the inverse appears, it will suffice to consider a non-relativistic example such as a temperatu ...
Relativistic Electrodynamics
... different reference frames moving with constant relative velocity ( inertial frames ) they will get exactly the same results. In another way, one can not perform an experiment in his own frame of reference that enables him to determine his speed with respect to another frame of reference without ref ...
... different reference frames moving with constant relative velocity ( inertial frames ) they will get exactly the same results. In another way, one can not perform an experiment in his own frame of reference that enables him to determine his speed with respect to another frame of reference without ref ...
Special Relativity
... mechanics, optics, electromagnetism and nuclear physics are the same in all inertial reference frames. Numerical values of quantities can be different, no acceleration (-> general relativity). 2) According to the principal of the constantcy of the velocity of light the speed of light in empty space ...
... mechanics, optics, electromagnetism and nuclear physics are the same in all inertial reference frames. Numerical values of quantities can be different, no acceleration (-> general relativity). 2) According to the principal of the constantcy of the velocity of light the speed of light in empty space ...
B = 1.2 T q, m proton: m = 1.67 x 10 kg q = e = 1.6 x 10 C v0 = 2 x 10
... If the speed of the proton has changed, what has happened to its kinetic energy? Can the Lorentz force cause such an effect? Because the Lorentz force is always ⊥ to the proton path, it does no work ⇒ no change in speed thus v = v0 = 2 × 108 m/s ...
... If the speed of the proton has changed, what has happened to its kinetic energy? Can the Lorentz force cause such an effect? Because the Lorentz force is always ⊥ to the proton path, it does no work ⇒ no change in speed thus v = v0 = 2 × 108 m/s ...
Relativistic Effects - The Physics of Bruce Harvey
... Maxwell had proved that the laws of electricity and magnetism predict the existence of electromagnetic waves which travel at the speed of light. But waves need something to wave and Maxwell called it the æther making use of an old Greek term. Sound travels through air and the speed of sound is affec ...
... Maxwell had proved that the laws of electricity and magnetism predict the existence of electromagnetic waves which travel at the speed of light. But waves need something to wave and Maxwell called it the æther making use of an old Greek term. Sound travels through air and the speed of sound is affec ...
Cross Product
... Torque Example T= R x F = RFsin() is the angle between the location of the applied force and the point where the radius meets this force. In this case, = 90, which means that the torque is just the product of the radius and the applied force because sin(90) = ...
... Torque Example T= R x F = RFsin() is the angle between the location of the applied force and the point where the radius meets this force. In this case, = 90, which means that the torque is just the product of the radius and the applied force because sin(90) = ...
relativity phys311
... Result of Galileian relativity: there is no mechanical experiment that can detect absolute motion, you can eat your dinner in an air plane (when it is not accelerating) which is moving rather fast with respect to the earth – just as well as on your dinner table at home – which is moving even faster ...
... Result of Galileian relativity: there is no mechanical experiment that can detect absolute motion, you can eat your dinner in an air plane (when it is not accelerating) which is moving rather fast with respect to the earth – just as well as on your dinner table at home – which is moving even faster ...
5. Electromagnetism and Relativity
... There are similar solutions associated to boosts along the y and z axes. The beauty of 4-vectors is that it’s extremely easy to write down invariant quantities. These are things which all observers, no matter which their reference frame, can agree on. To construct these we take the inner product of ...
... There are similar solutions associated to boosts along the y and z axes. The beauty of 4-vectors is that it’s extremely easy to write down invariant quantities. These are things which all observers, no matter which their reference frame, can agree on. To construct these we take the inner product of ...
Uniform and constant electromagnetic fields
... Taking the cross product with B finally obtain ~vd = ...
... Taking the cross product with B finally obtain ~vd = ...
Electric and magnetic field transformations Picture: Consider inertial frames
... Ex = E’x = 0 Ey = γ E’y Ez = γ E’z E = γλ/(2πε0 r’) { (y’/r’) j + (z’/r’) k } E = γλ/(2πε0 r) { (y/r) j + (z/r) k } ; this is the same as a line of charge with density γλ, larger than λ because of Lorentz contraction. ...
... Ex = E’x = 0 Ey = γ E’y Ez = γ E’z E = γλ/(2πε0 r’) { (y’/r’) j + (z’/r’) k } E = γλ/(2πε0 r) { (y/r) j + (z/r) k } ; this is the same as a line of charge with density γλ, larger than λ because of Lorentz contraction. ...
When and Where is a Current Electrically Neutral?
... on v2. This means that the plus ions are bunched together a bit, so that their density is increased. The result is a net preponderance of positive charge in the wire, so that it ceases to be electrically neutral. Consequently a non-vanishing radial E-field is present in S’, due to Lorentz contractio ...
... on v2. This means that the plus ions are bunched together a bit, so that their density is increased. The result is a net preponderance of positive charge in the wire, so that it ceases to be electrically neutral. Consequently a non-vanishing radial E-field is present in S’, due to Lorentz contractio ...
Lagrangians
... 2 Fully covariant theory Now the problem with this formalism is that it contains the coordinate time To have a fully covariant theory we will need to reformulate it in terms of the proper time We start with the action for a free particle (a particle moving in a field-free region). The integra ...
... 2 Fully covariant theory Now the problem with this formalism is that it contains the coordinate time To have a fully covariant theory we will need to reformulate it in terms of the proper time We start with the action for a free particle (a particle moving in a field-free region). The integra ...
Moving from Newton to Einstein
... In the late eighteenth century a Scottish mathematician, Maxwell, discovered the laws of electromagnetism which allowed physicists to formulate a wave equation for light and other electromagnetic radiation. They jumped to the conclusion that light, like sound and other waves must be propagated in a ...
... In the late eighteenth century a Scottish mathematician, Maxwell, discovered the laws of electromagnetism which allowed physicists to formulate a wave equation for light and other electromagnetic radiation. They jumped to the conclusion that light, like sound and other waves must be propagated in a ...