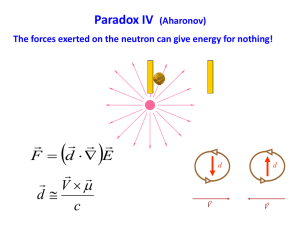
Time Symmetry and the Many-Worlds Interpretation - Philsci
... The MWI in Stanford Philosophy Encyclopedia [14] I will now clarify (and slightly amend) this definition. First, a world is not a concept associated with a particular moment in time, but with all of time. It is a complete history in which all macroscopic objects have definite states. At the beginnin ...
... The MWI in Stanford Philosophy Encyclopedia [14] I will now clarify (and slightly amend) this definition. First, a world is not a concept associated with a particular moment in time, but with all of time. It is a complete history in which all macroscopic objects have definite states. At the beginnin ...
Nature 425, (937
... 2 j1lj j1ljþ1 þ 2 jBELLl: Here jBELLl denotes the Belllike state corresponding to ðj0lj ðj0ljþ1 2 j1ljþ1 Þ þ j1lj ðj0ljþ1 þ j1ljþ1 ÞÞ=2: This scheme can be generalized when more than two particles are placed next to each other, starting from a Mott insulating state of matter9,10. In such a Mott insu ...
... 2 j1lj j1ljþ1 þ 2 jBELLl: Here jBELLl denotes the Belllike state corresponding to ðj0lj ðj0ljþ1 2 j1ljþ1 Þ þ j1lj ðj0ljþ1 þ j1ljþ1 ÞÞ=2: This scheme can be generalized when more than two particles are placed next to each other, starting from a Mott insulating state of matter9,10. In such a Mott insu ...
On Gauge Invariance and Covariant Derivatives in Metric Spaces
... Here, R′ µνα is the Riemann curvature tensor associated with the derivative ∇′µ in Eq.(9), and is given by the familiar expression in terms of ordinary partial derivatives of Γα µν [2]. In the following, we will find that the Palatini formulation is consistent with a general quantum theory of gravit ...
... Here, R′ µνα is the Riemann curvature tensor associated with the derivative ∇′µ in Eq.(9), and is given by the familiar expression in terms of ordinary partial derivatives of Γα µν [2]. In the following, we will find that the Palatini formulation is consistent with a general quantum theory of gravit ...
Compact convergence does not imply local uniform
... Suppose fn : X → Y is a sequence (or a net) of functions from a topological space X into a uniform space Y (e.g. a metric space). Then fn is locally uniformly convergent if every point of X has a neighborhood V such that fn is uniformly convergent on V , and fn is compactly convergent if fn is unifo ...
... Suppose fn : X → Y is a sequence (or a net) of functions from a topological space X into a uniform space Y (e.g. a metric space). Then fn is locally uniformly convergent if every point of X has a neighborhood V such that fn is uniformly convergent on V , and fn is compactly convergent if fn is unifo ...
Hypergroups and Quantum Bessel Processes of Non
... The dimension of the Bessel process with index µ is δ = 2(µ + 1) and a common notation for the Bessel process with the dimension δ is BES(δ). It is well known that the notion of the Bessel process makes sense for any real number δ and that the Bessel processes of integer dimension δ ≥ 2 are the radi ...
... The dimension of the Bessel process with index µ is δ = 2(µ + 1) and a common notation for the Bessel process with the dimension δ is BES(δ). It is well known that the notion of the Bessel process makes sense for any real number δ and that the Bessel processes of integer dimension δ ≥ 2 are the radi ...
arXiv:1504.04012v1 [cond-mat.quant
... far, this is a well-defined quantum number since the cosine term in Eq. (5) transfers only pairs of bosons from the condensate. Note that N takes 2m distinct eigenvalp ues. This allows us to associate a degeneracy of 2m with each of the endpoints of the BEC trench (the ‘defects’) in the limit of a l ...
... far, this is a well-defined quantum number since the cosine term in Eq. (5) transfers only pairs of bosons from the condensate. Note that N takes 2m distinct eigenvalp ues. This allows us to associate a degeneracy of 2m with each of the endpoints of the BEC trench (the ‘defects’) in the limit of a l ...