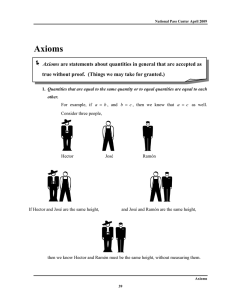
Numbers, proof and `all that jazz`.
... Since the time of Euclid, lists of axioms for many fields of mathematics, such as set theory, logic, and numbers have been compiled. In these notes, we present one of the standard lists of axioms for the real numbers, which are the numbers used in calculus. Thus, we are stating “up front,” those pro ...
... Since the time of Euclid, lists of axioms for many fields of mathematics, such as set theory, logic, and numbers have been compiled. In these notes, we present one of the standard lists of axioms for the real numbers, which are the numbers used in calculus. Thus, we are stating “up front,” those pro ...
Natural Deduction Proof System
... • Natural Deduction tries to follow the natural style of reasoning. Most of the proof consists of forward reasoning, i.e. deriving conclusions, deriving new conclusions from these conclusions, etc. Occasionally hypotheses are introduced or dropped. • A derivation is a tree where the nodes are the ru ...
... • Natural Deduction tries to follow the natural style of reasoning. Most of the proof consists of forward reasoning, i.e. deriving conclusions, deriving new conclusions from these conclusions, etc. Occasionally hypotheses are introduced or dropped. • A derivation is a tree where the nodes are the ru ...
We showed on Tuesday that Every relation in the arithmetical
... Gödel’s First Incompleteness Theorem essentially states that no reasonable axiom system can “capture” all arithmetic truth , because the set True is not semidecidable. To illustrate the theorem we need some definitions and observations. ...
... Gödel’s First Incompleteness Theorem essentially states that no reasonable axiom system can “capture” all arithmetic truth , because the set True is not semidecidable. To illustrate the theorem we need some definitions and observations. ...
Multi-Agent Only
... Levesque considered only the single-agent case. I Compelling (i.e. simple) model-theoretic account I I ...
... Levesque considered only the single-agent case. I Compelling (i.e. simple) model-theoretic account I I ...
Relating Infinite Set Theory to Other Branches of Mathematics
... termination proofs depend on showing that the state corresponds to a descending sequence of infinite ordinals. I had never seen this, and would not have thought it possible. Leaving infinite sets for a while, Stillwell turns in chapters 3 and 4 to computation and undecidability theory. These chapter ...
... termination proofs depend on showing that the state corresponds to a descending sequence of infinite ordinals. I had never seen this, and would not have thought it possible. Leaving infinite sets for a while, Stillwell turns in chapters 3 and 4 to computation and undecidability theory. These chapter ...
MATH 532, 736I: MODERN GEOMETRY
... Part III. The problems in this section all deal with an axiomatic system consisting of the axioms below. Be sure to answer the questions being asked. For example, if you are giving a model to justify your answer in problem (1) below, make sure you also state whether your answer is, “Yes” or “No.” T ...
... Part III. The problems in this section all deal with an axiomatic system consisting of the axioms below. Be sure to answer the questions being asked. For example, if you are giving a model to justify your answer in problem (1) below, make sure you also state whether your answer is, “Yes” or “No.” T ...
CHAP02 Axioms of Set Theory
... We can define x+ = {x, {x}} and hence we can define the integers by considering n+ as n + 1 (though addition and multiplication would yet have to be defined). In the early 1900s as the great philosopher Frege was preparing the second volume of his book on the foundations of mathematics, building eve ...
... We can define x+ = {x, {x}} and hence we can define the integers by considering n+ as n + 1 (though addition and multiplication would yet have to be defined). In the early 1900s as the great philosopher Frege was preparing the second volume of his book on the foundations of mathematics, building eve ...
Logic and Proof - Collaboratory for Advanced Computing and
... 2. Given two distinct points, one can draw one and only one circle centered at the first point and passing through the second one. 3. Any two right angles are equal. 4. Every line segment can be infinitely continued in either direction. 5. For any given line l and a point P not on that lin ...
... 2. Given two distinct points, one can draw one and only one circle centered at the first point and passing through the second one. 3. Any two right angles are equal. 4. Every line segment can be infinitely continued in either direction. 5. For any given line l and a point P not on that lin ...
FOR HIGHER-ORDER RELEVANT LOGIC
... a normal R2-theory that does not contain A. Normality here is taken in quite a strong sense. A normal R2-theory must contain all theorems of R2 (whatever choice we havemade among potential axioms [C] and their n-ary analogues); moreover, it must respect all the connectives and quantifiers, being con ...
... a normal R2-theory that does not contain A. Normality here is taken in quite a strong sense. A normal R2-theory must contain all theorems of R2 (whatever choice we havemade among potential axioms [C] and their n-ary analogues); moreover, it must respect all the connectives and quantifiers, being con ...
IntroToLogic - Department of Computer Science
... The validity of first order logic is not decidable. (It is semi-decidable.) If a theorem is logically entailed by an axiom, you can prove that it is. But if it is not, you can’t necessarily prove that it is not. (You may go on infinitely with your proof.) ...
... The validity of first order logic is not decidable. (It is semi-decidable.) If a theorem is logically entailed by an axiom, you can prove that it is. But if it is not, you can’t necessarily prove that it is not. (You may go on infinitely with your proof.) ...
Introduction to Discrete Mathematics
... Given a digital circuit, we can construct the truth table. Now, suppose we are given only the truth table (i.e. the specification), how can we construct a circuit (i.e. formula) that has the same function? ...
... Given a digital circuit, we can construct the truth table. Now, suppose we are given only the truth table (i.e. the specification), how can we construct a circuit (i.e. formula) that has the same function? ...