The Quantum Circuit Model and Universal Quantum Computation
... there are. For example there are computer models called hypercomputation which explicitly compute non-Turingcomputable functions. But we call these models not reasonable because I know of no way to physically construct these devices (although certainly some have tried.) The lesson, of course, is tha ...
... there are. For example there are computer models called hypercomputation which explicitly compute non-Turingcomputable functions. But we call these models not reasonable because I know of no way to physically construct these devices (although certainly some have tried.) The lesson, of course, is tha ...
Characterizing the Performance Effect of Trials and Rotations in
... algorithms. Intuitively, QPE allows quantum algorithms to find the hidden structure in certain kinds of problems. In particular, Shor’s well-known algorithm for factoring the product of two primes uses QPE. Simulation algorithms, such as Ground State Estimation (GSE) for quantum chemistry, also use ...
... algorithms. Intuitively, QPE allows quantum algorithms to find the hidden structure in certain kinds of problems. In particular, Shor’s well-known algorithm for factoring the product of two primes uses QPE. Simulation algorithms, such as Ground State Estimation (GSE) for quantum chemistry, also use ...
Lecture 10
... momentum, denoted as L. This vector has the same direction as v. The linear momentum vector has units of (kg·m)/s or (slug·ft)/s. Linear impulse: The integral F dt is the linear impulse, denoted I. It is a vector quantity measuring the effect of a force during its time interval of action. I acts in ...
... momentum, denoted as L. This vector has the same direction as v. The linear momentum vector has units of (kg·m)/s or (slug·ft)/s. Linear impulse: The integral F dt is the linear impulse, denoted I. It is a vector quantity measuring the effect of a force during its time interval of action. I acts in ...
Dissociation energy of the water dimer from Quantum Monte Carlo
... lation potential (VWN) is used to extract the local part of the LYP correlation potential. The usual B3LYP functional corresponds to A = 0.2, B = 0.9 and C = 0.81. In principle we could try and minimize the DMC energy with respect to A, B and C, but this would be very expensive. Setting A = 1 in Eq ...
... lation potential (VWN) is used to extract the local part of the LYP correlation potential. The usual B3LYP functional corresponds to A = 0.2, B = 0.9 and C = 0.81. In principle we could try and minimize the DMC energy with respect to A, B and C, but this would be very expensive. Setting A = 1 in Eq ...
Quantum measurements of coupled systems * L. Fedichkin, M. Shapiro,
... However, it is not of a QNDM type, both the amplitude and the phase of the excitation wave function are changed. The problem of measuring coupled qubits is related to the problem of localization. Localization of single-excitation stationary states is well understood since Anderson’s work 关4兴 on diso ...
... However, it is not of a QNDM type, both the amplitude and the phase of the excitation wave function are changed. The problem of measuring coupled qubits is related to the problem of localization. Localization of single-excitation stationary states is well understood since Anderson’s work 关4兴 on diso ...
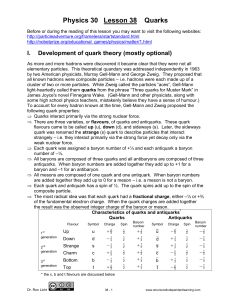
Physics 30 - Structured Independent Learning
... The difficulty was soon settled by appealing to an idea, suggested by a DanishAmerican physicist named Sheldon L. Glashow, that had been around for some time but had found little support. Because there were then four known leptons, it had been proposed (on the grounds of natural symmetry among eleme ...
... The difficulty was soon settled by appealing to an idea, suggested by a DanishAmerican physicist named Sheldon L. Glashow, that had been around for some time but had found little support. Because there were then four known leptons, it had been proposed (on the grounds of natural symmetry among eleme ...
- D-Wave Systems
... format and many real-world problems can be easily mapped to it. However, QUBO instances arising from real-world problems do not necessarily match the constrained size and connectivity of a given system. We describe a solver, qbsolv, that reads a QUBO instance in a general format, partitions it into ...
... format and many real-world problems can be easily mapped to it. However, QUBO instances arising from real-world problems do not necessarily match the constrained size and connectivity of a given system. We describe a solver, qbsolv, that reads a QUBO instance in a general format, partitions it into ...
Detected-jump-error-correcting quantum codes - IAP TU
... subspace. For a given number of N qubits the dimension K D of such a decoherence-free subspace is given by K D ⫽( wN ) which is maximal if w⫽ b N/2c . ( b x c denotes the largest integer smaller or equal to x.兲 In general, the first spontaneous emission of a photon will affect the quantum state of t ...
... subspace. For a given number of N qubits the dimension K D of such a decoherence-free subspace is given by K D ⫽( wN ) which is maximal if w⫽ b N/2c . ( b x c denotes the largest integer smaller or equal to x.兲 In general, the first spontaneous emission of a photon will affect the quantum state of t ...
Exact quantum query complexity
... EXACT2 on 3 bits. For the other functions on 3 bits (x1 ∧ (x2 ∨ x3 ) and (x1 ∧ x2 ) ∨ (x¯1 ∧ x¯2 ∧ x3 )) we also found explicit exact quantum query algorithms. This was via a somewhat painful process of manually rounding real-valued solutions to the SDP to produce rational, exact solutions. But coul ...
... EXACT2 on 3 bits. For the other functions on 3 bits (x1 ∧ (x2 ∨ x3 ) and (x1 ∧ x2 ) ∨ (x¯1 ∧ x¯2 ∧ x3 )) we also found explicit exact quantum query algorithms. This was via a somewhat painful process of manually rounding real-valued solutions to the SDP to produce rational, exact solutions. But coul ...
Generation of arbitrary Dicke states in spinor Bose±Einstein
... a spinor condensate due to the internal nonlinear atom±atom interaction [30]. In this note, we extend these results by describing a quantum control technique which allows to prepare arbitrary Dicke spin states, as well as maximally entangled states by means of properly sequencing of external couplin ...
... a spinor condensate due to the internal nonlinear atom±atom interaction [30]. In this note, we extend these results by describing a quantum control technique which allows to prepare arbitrary Dicke spin states, as well as maximally entangled states by means of properly sequencing of external couplin ...
The Physical Implementation of Quantum Computation David P. DiVincenzo
... by a measurement which projects the system either into the state desired or another state which can be rotated into it. These approaches are not fundamentally different from one another, since the projection procedure is a form of cooling; for instance, the laser cooling techniques used routinely no ...
... by a measurement which projects the system either into the state desired or another state which can be rotated into it. These approaches are not fundamentally different from one another, since the projection procedure is a form of cooling; for instance, the laser cooling techniques used routinely no ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.